初中数学北师大版（2024）九年级下册5 二次函数与一元二次方程精品课件ppt

这是一份初中数学北师大版（2024）九年级下册5 二次函数与一元二次方程精品课件ppt，共22页。PPT课件主要包含了有两个交点，两个相异的实根，b2-4ac0，有一个交点，两个相等的实根，没有交点，没有实数根，横坐标，典型例题，知识要点等内容，欢迎下载使用。
1.利用二次函数的图象求一元二次方程近似解.（重点）2.经历探索用二次函数图象求解一元二次方程近似解的过程，体会用二次函数函数图象求一元二次方程解的方法.（难点）
1.二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
2.抛物线y＝ax2＋bx＋c与x轴交点的 就是一元二次方程ax2＋bx＋c＝0的根．
一元二次方程x2＋2x－10＝0的根是二次函数y＝x2＋2x－10的图象与x轴交点的横坐标．
这样，我们在不解方程的情况下，只要知道二次函数图象与x轴交点的横坐标即可，但是根据图象我们很难准确地求出方程的解，所以要进行估算，本节课我们将学习利用二次函数的图象求一元二次方程的近似根．
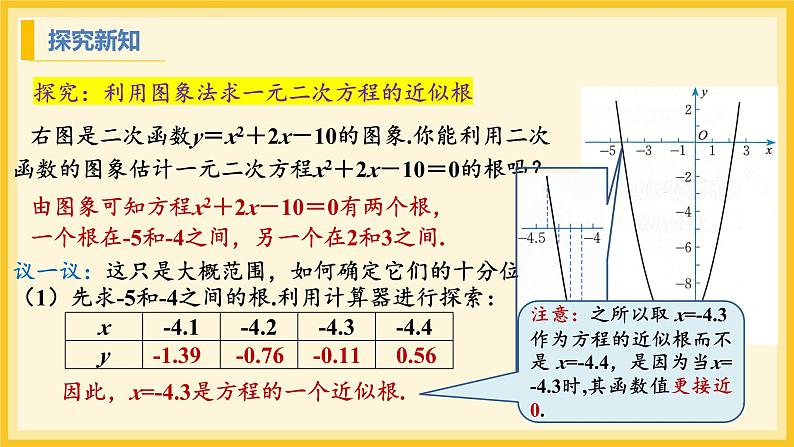
探究：利用图象法求一元二次方程的近似根
由图象可知方程x2＋2x－10＝0有两个根，一个根在-5和-4之间，另一个在2和3之间.
议一议：这只是大概范围，如何确定它们的十分位呢？（1）先求-5和-4之间的根.利用计算器进行探索：
-1.39 -0.76 -0.11 0.56
因此，x=-4.3是方程的一个近似根.
注意：之所以取 x=-4.3 作为方程的近似根而不是 x=-4.4，是因为当x=-4.3时,其函数值更接近0.
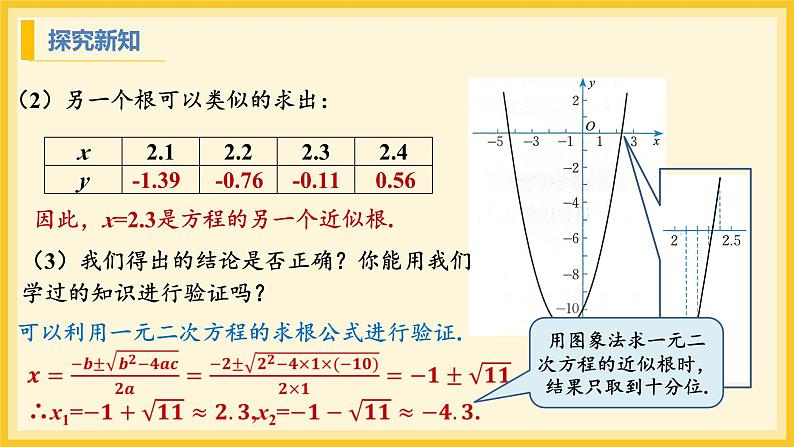
（2）另一个根可以类似的求出：
因此，x=2.3是方程的另一个近似根.
（3）我们得出的结论是否正确？你能用我们学过的知识进行验证吗？
可以利用一元二次方程的求根公式进行验证.
用图象法求一元二次方程的近似根时，结果只取到十分位.
例1：利用二次函数的图象估计一元二次方程x2－2x－1＝0的近似根(结果精确到0.1)．
解：方程x2－2x－1＝0的根是函数y＝x2－2x－1的图象与x轴交点的横坐标．作出二次函数y＝x2－2x－1的图象，如图所示.由图象可知方程有两个根，一个在－1和0之间，另一个在2和3之间.
先求－1和0之间的根，当x＝－0.4时，y＝－0.04；当x＝－0.5时，y＝0.25.因此，x≈－0.4是方程的一个近似根， 同理，x≈2.4是方程的另一个近似根.即方程x2－2x－1＝0的近似根为x1≈－0.4，x2≈2.4.
(1)画出二次函数的图象；(2)确定抛物线与x轴的交点的横坐标在哪两个数之间；(3)列表或直接取值代入方程计算，哪一个值能使方程近似成立，则这个值就是方程的近似根．
利用图象法求一元二次方程的近似根
求一元二次方程x2+2x-10=3的近似根，即求方程x2+2x-13=0的近似根.也就是估计抛物线y=x2+2x-13和x轴的交点的横坐标；
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7.
∴方程x2+2x-10=3的近似根为：x1≈-4.7，x2≈2.7.
①作直线y=3；②观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标；由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
分析：当 y＝－x2＋2x－3的函数值为－8时，对应点的横坐标即为一元二次方程－x2＋2x－3＝－8的根，如图所示．
例3：利用二次函数的图象求一元二次方程－x 2＋2x－3＝－8的近似根．
解：在平面直角坐标系内作函数 y＝－x 2＋2x－3的图象，如图，由图象可知方程－x 2＋2x－3＝－8的根是抛物线y＝－x 2＋2x－3与直线y＝－8的公共点的横坐标，左边的公共点横坐标在－1与－2之间，右边的公共点横坐标在3和4之间．
(1)先求在－1和－2之间的根，利用计算器进行探索：
∴x＝－1.4是方程－x2＋2x－3＝－8的一个近似根．
(2)另一根可以类似地求出：
∴x＝3.4是方程－x2＋2x－3＝－8的另一个近似根．
一元二次方程－x 2＋2x－3＝－8的近似根为：x1≈-1.4，x2≈3.4.
那么方程x2＋3x－5＝0的一个近似根是(　 　)A.1 B.1.1 C.1.2 D.1.3
1.下表是一组二次函数y＝x2＋3x－5的自变量x与函数值y的对应值：
2.下表是满足二次函数y＝ax2＋bx＋c的五组数据，x1是方程ax2＋bx＋c＝0的一个解，则下列选项中正确的是(　　)
A.1.6＜x1＜1.8B.1.8＜x1＜＜x1＜2.2D.2.2＜x1＜2.4
3.观察下表:则一元二次方程x2－2x－2＝0在精确到0.1时的一个近似根是 ，利用抛物线的对称性，可推知该方程的另一个近似根是 .
5.用图象法求一元二次方程x2+x-1＝0的近似根（精确到0.1）.
解：画出x2+x-1=0的图象，如图所示，由图象知，方程有两个根，一个在-2和-1之间，另一个在0到1之间.通过计算器估算，可得到抛物线与x轴交点的横坐标大约为-1.6和0.6.即一元二次方程的实数根为x1≈-1.6，x2≈0.6.
利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤是怎样的？
①用描点法作二次函数y=ax2+bx+c的图象；
②观察估计二次函数的图象与x轴的交点的横坐标；
③确定一元二次方程ax2+bx+c=0的解。
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是（ ） A. 3< x < 3.23 B. 3.23 < x < 3.24 C. 3.24