数学九年级下册第三章 圆7 切线长定理优秀ppt课件

这是一份数学九年级下册第三章 圆7 切线长定理优秀ppt课件，共26页。PPT课件主要包含了内切圆，角平分线，探究一切线长的定义，探究二切线长定理，知识要点，典型例题，△APB△AOB，2连接两切点，方法归纳，还有没有其他解法等内容，欢迎下载使用。
1.掌握切线长定理，初步学会运用切线长定理进行计算与证明.（重点）2.了解三角形的内切圆和三角形的内心的概念.3.学会利用方程思想解决几何问题，体验数形结合思想.（难点）
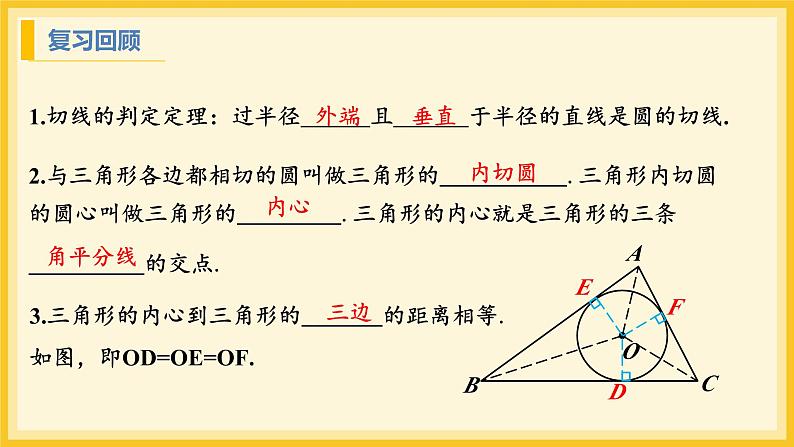
1.切线的判定定理：过半径 且 于半径的直线是圆的切线.
2.与三角形各边都相切的圆叫做三角形的 .三角形内切圆的圆心叫做三角形的 .三角形的内心就是三角形的三条 的交点.
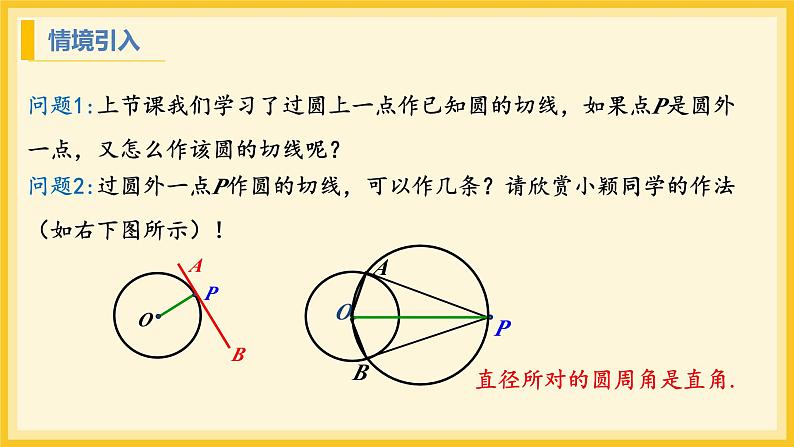
问题1:上节课我们学习了过圆上一点作已知圆的切线，如果点P是圆外一点，又怎么作该圆的切线呢？
直径所对的圆周角是直角.
问题2:过圆外一点P作圆的切线，可以作几条？请欣赏小颖同学的作法（如右下图所示）！
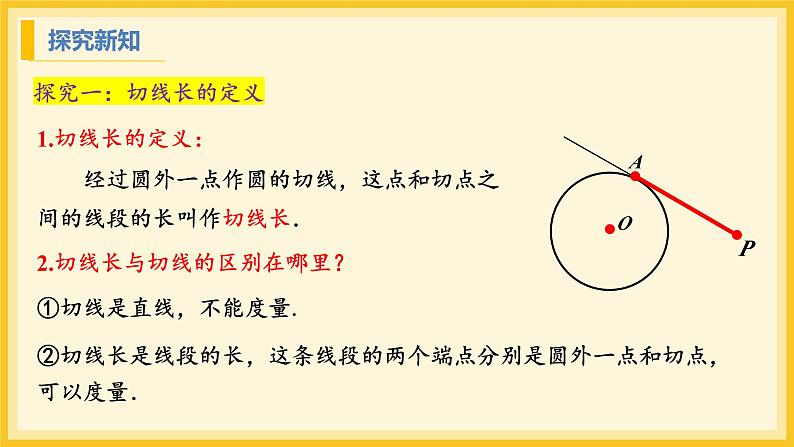
1.切线长的定义： 经过圆外一点作圆的切线，这点和切点之间的线段的长叫作切线长．
①切线是直线，不能度量.
②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量．
2.切线长与切线的区别在哪里？
这个图形是轴对称图形，它的对称轴是点P，O所在的直线．
（2）在这个图形中你能找到相等的线段吗？说说你的理由.
PA＝PB，因为这个图形是轴对称图形，根据其性质“对应线段相等” 就可以得出PA＝PB．也可以利用三角形全等来证明.
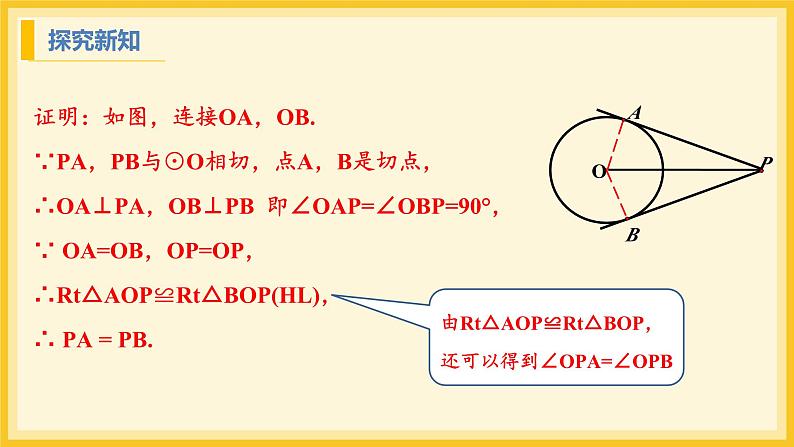
证明：如图，连接OA，OB.∵PA，PB与⊙O相切，点A，B是切点，∴OA⊥PA，OB⊥PB 即∠OAP=∠OBP=90°，∵ OA=OB，OP=OP，∴Rt△AOP≌Rt△BOP(HL)，∴ PA = PB.
由Rt△AOP≌Rt△BOP，还可以得到∠OPA=∠OPB
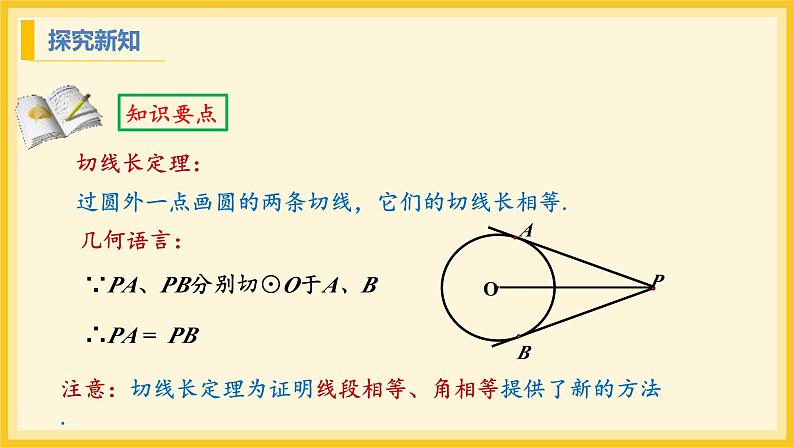
切线长定理：过圆外一点画圆的两条切线，它们的切线长相等.
注意：切线长定理为证明线段相等、角相等提供了新的方法.
OA⊥PA，OB ⊥PB，AB ⊥OP.
△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP.
∠OAC=∠OBC=∠APC=∠BPC.
解析：连接OA、OB、OC、OD和OE.∵PA、PB是☉O的两条切线，点A、B是切点，∴PA=PB=7.∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-∠PBO-∠P=140°.
又∵DC、DA是☉O的两条切线，点C、A是切点，∴DC=DA.同理可得CE=EB.l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
★切线长问题辅助线添加方法
（3）连接圆心和圆外一点.
（1）分别连接圆心和切点；
∵ 四边形ABCD为圆外切四边形，根据切线长定理可得：AH＝AE，BE＝BF，CF＝CG，DG＝DH．
图中线段还有其他的等量关系吗？
AH+DH+BF+CF＝AE+DG+BE+CG,即AD+BC=AB+CD．
归纳：圆的外切四边形的两组对边之和相等．
4.如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠ACB＝70°，那么∠OPA的度数是______°．
3.如图，AD，DC，BC都与⊙O相切，且AD∥BC，则∠DOC＝ °．
5.△ABC的内切圆⊙O与三边分别切于D、E、F三点，如图，已知AF=3, BD+CE=12, 则△ABC的周长是 .
解：∵ AC，AP为⊙O的切线，∴ AC＝AP．∵ BP，BD为⊙O的切线，∴ BP＝BD，∴ BD＝PB＝AB－AP＝5－3＝2．
65 °或115 °
解：设AF=x,则AE=x
∴CD=CE=AC-AE=13-x，BD=BF=AB-AF=9-x.
由BD+CD=BC可得13-x+9-x=14，
∴ AF=4 cm, BD=5 cm, CE=9 cm.
教材习题3.9；