中考数学二轮复习压轴题培优训练专题10胡不归问题（2份，原卷版+解析版）

这是一份中考数学二轮复习压轴题培优训练专题10胡不归问题（2份，原卷版+解析版），文件包含中考数学二轮复习压轴题培优训练专题10胡不归问题原卷版doc、中考数学二轮复习压轴题培优训练专题10胡不归问题解析版doc等2份试卷配套教学资源，其中试卷共84页， 欢迎下载使用。

“PA＋k·PB”型的最值问题，当k＝1时通常为轴对称之最短路径问题，而当k＞0时，若以常规的轴对称的方式解决，则无法进行，因此必须转换思路．
当点P在直线上
如图，直线BM，BN交于点B，P为BM上的动点，点A在射线BM，BN同侧，已知sin∠MBN＝k．
过点A作AC⊥BN于点C，交BM于点P，此时PA＋k·PB取最小值，最小值即为AC的长．

证明 如图，在BM上任取一点Q，连结AQ，作QD⊥BN于点D．
由sin∠MBN＝k，可得QD＝ k·QB．
所以QA＋k·QB＝QA＋QD≥AC，即得证．
2． 当点P在圆上
如图，⊙O的半径为r，点A，B都在⊙O外，P为⊙O上的动点，已知r＝k·OB．
在OB上取一点C，使得OC＝ k·r，连结AC交⊙O于点P，此时PA＋k·PB取最小值，最小值即为AC的长．

证明 如图，在⊙O上任取一点Q，连结AQ，BQ，连结CQ，OQ．
则OC＝ k·OQ，OQ＝ k·OB．
而∠COQ＝∠QOB，所以△COQ∽△QOB，
所以QC＝ k·QB．
所以QA＋ k·QB ＝QA＋QC≥AC，即得证．
经典例题
【例1】（2021·全国·九年级专题练习）如图，在平面直角坐标系中，二次函数y＝ax2＋bx＋c的图象经过点A（﹣1，0），B（0，），C（2，0），其对称轴与x轴交于点D．
（1）求二次函数的表达式及其顶点坐标；
（2）点M为抛物线的对称轴上的一个动点，若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，求点M的坐标；
（3）若P为y轴上的一个动点，连接PD，求PB＋PD的最小值．
【例2】（2022·重庆·八年级期末）已知，在正方形ABCD中，点E，F分别为AD上的两点，连接BE、CF，并延长交于点G，连接DG，H为CF上一点，连接BH、DH，
(1)如图1，若H为CF的中点，且，，求线段AB的长；
(2)如图2，若，过点B作于点I，求证：；
(3)如图2，在（1）的条件下，P为线段AD（包含端点A、D）上一动点，连接CP，过点B作于点Q，将沿BC翻折得，N为直线AB上一动点，连接MN，当面积最大时，直接写出的最小值．
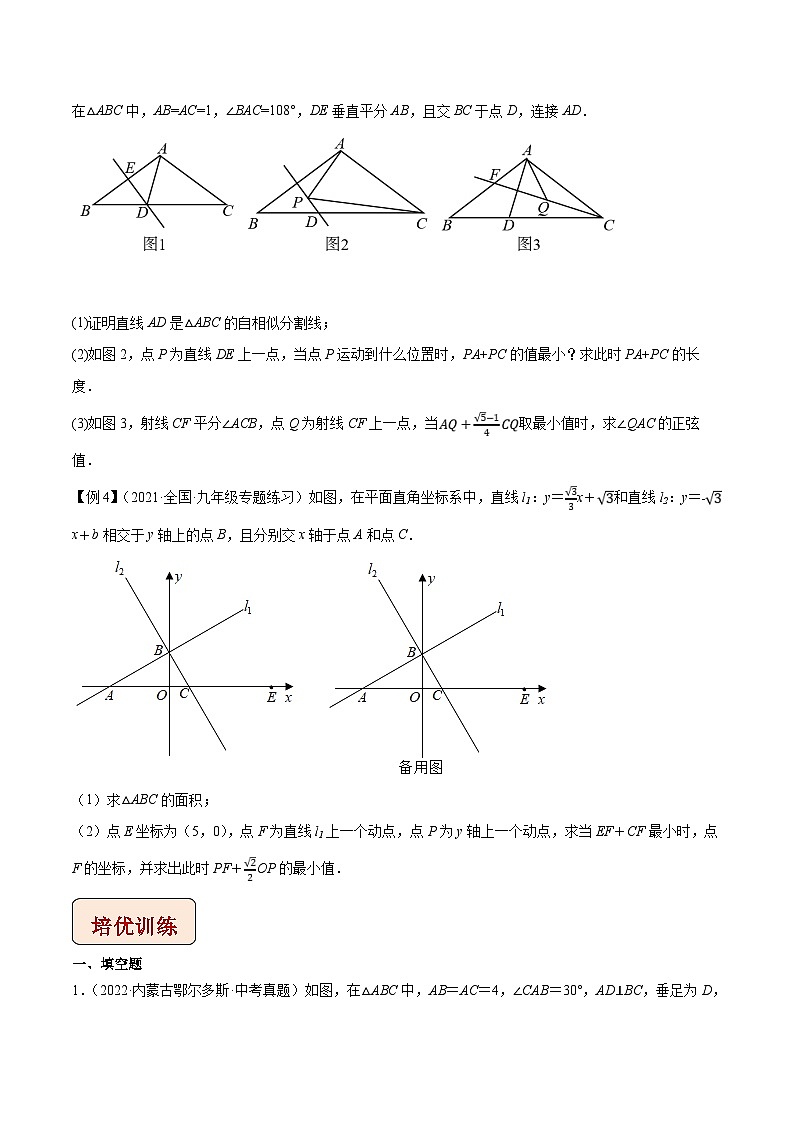
【例3】（2022·湖南师大附中博才实验中学九年级开学考试）如果有一条直线经过三角形的某个顶点，将三角形分成两个三角形，其中一个三角形与原三角形相似，则称该直线为三角形的“自相似分割线”．如图1，在△ABC中，AB=AC=1，∠BAC=108°，DE垂直平分AB，且交BC于点D，连接AD．
(1)证明直线AD是△ABC的自相似分割线；
(2)如图2，点P为直线DE上一点，当点P运动到什么位置时，PA+PC的值最小？求此时PA+PC的长度．
(3)如图3，射线CF平分∠ACB，点Q为射线CF上一点，当取最小值时，求∠QAC的正弦值．
【例4】（2021·全国·九年级专题练习）如图，在平面直角坐标系中，直线l1：y＝x＋和直线l2：y＝﹣x＋b相交于y轴上的点B，且分别交x轴于点A和点C．
（1）求△ABC的面积；
（2）点E坐标为（5，0），点F为直线l1上一个动点，点P为y轴上一个动点，求当EF＋CF最小时，点F的坐标，并求出此时PF＋OP的最小值．
培优训练
一、填空题
1．（2022·内蒙古鄂尔多斯·中考真题）如图，在△ABC中，AB＝AC＝4，∠CAB＝30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC．则PA+2PB的最小值为 _____．
2．（2022·湖北湖北·八年级期末）如图，▱中，，，为边上一点，则的最小值为______．
3．（2022·湖北武汉·一模）如图，在中，，，半径为的经过点，是圆的切线，且圆的直径在线段上，设点是线段上任意一点不含端点，则的最小值为______．
4．（2022·湖北武汉·九年级阶段练习）如图，在△ACE中，CA＝CE，∠CAE＝30°，半径为5的⊙O经过点C，CE是圆O的切线，且圆的直径AB在线段AE上，设点D是线段AC上任意一点（不含端点），则ODCD的最小值为 _____．
5．（2021·江苏·苏州高新区实验初级中学九年级阶段练习）如图，正方形ABCD的边长为4，点E为边AD上一个动点，点F在边CD上，且线段EF＝4，点G为线段EF的中点，连接BG、CG，则BG+CG的最小值为 _____．
6．（2021·四川省成都市七中育才学校八年级期中）如图，在平面直角坐标系中，直线l分别交x、y轴于B、C两点，点A、C的坐标分别为(3，0)、(0，﹣3)，且∠OCB＝60°，点P是直线l上一动点，连接AP，则的最小值是______．
7．（2021·全国·九年级专题练习）如图，直线y＝x﹣3分别交x轴、y轴于B、A两点，点C（0，1）在y轴上，点P在x轴上运动，则PC＋PB的最小值为___．
8．（2021·全国·九年级专题练习）如图，矩形ABCD中AB＝3，BC，E为线段AB上一动点，连接CE，则AE＋CE的最小值为___．
9．（2021·四川·成都市树德实验中学八年级期末）如图，△ABC中，∠BAC＝75°，∠ACB＝60°，AC＝4，则△ABC的面积为_；点D，点E，点F分别为BC，AB，AC上的动点，连接DE，EF，FD，则△DEF的周长最小值为_．
10．（2021·全国·九年级专题练习）如图，在边长为4的正方形ABCD内有一动点P，且BP＝．连接CP，将线段PC绕点P逆时针旋转90°得到线段PQ．连接CQ、DQ，则DQ+CQ的最小值为 ___．
11．（2021·全国·九年级专题练习）如图，四边形ABCD是菱形，AB＝8，且∠ABC＝60°，M为对角线BD（不含B点）上任意一点，则AM+BM的最小值为_____．
12．（2021·全国·九年级专题练习）如图，▱ABCD中，∠DAB＝30°，AB＝6，BC＝2，P为边CD上的一动点，则2PB+ PD的最小值等于______.
13．（2022·四川自贡·一模）如图，中，，，于点，是线段上的一个动点，则的最小值是__________．
14．（2021·全国·九年级专题练习）如图，抛物线与x轴交于A、B两点，过B的直线交抛物线于E，且tan∠EBA=，有一只蚂蚁从A出发，先以1单位/s的速度爬到线段BE上的点D处，再以1.25单位/s的速度沿着DE爬到E点处觅食，则蚂蚁从A到E的最短时间是________s．
二、解答题
15．（2022·全国·九年级）如图，在平面直角坐标系中，直线y＝x＋2与x轴交于点A，与y轴交于点C．抛物线y＝ax2＋bx＋c的对称轴是x＝－且经过A、C两点，与x轴的另一交点为点B．

(1)求二次函数y＝ax2＋bx＋c的表达式；
(2)点P为线段AB上的动点，求AP＋2PC的最小值；
(3)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A，M，N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
16．（2022·四川眉山·九年级专题练习）如图1，在平面直角坐标系中，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．
(1)求A、C两点的坐标；
(2)连接AC，点P为直线AC上方抛物线上（不与A、C重合）的一动点，过点P作PD⊥AC交AC于点D，PE⊥x轴交AC于点E，求PD+DE的最大值及此时点P的坐标；
(3)如图2，将原抛物线沿射线CB方向平移3个单位得到新抛物线y'，点M为新抛物线y'对称轴上一点，在新抛物线y'上是否存在一点N，使以点C、A、M、N为顶点的四边形为平行四边形，若存在，请直接写出点M的坐标，并选择一个你喜欢的点写出求解过程；若不存在，请说明理由．
17．（2022·湖南长沙·八年级阶段练习）如图1，抛物线与x轴交于点，与y轴交于点B，在x轴上有一动点（），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．
(1)求a的值和直线AB的函数表达式：
(2)设△PMN的周长为，△AEN的周长为，若求m的值．
(3)如图2，在（2）的条件下，将线段OE绕点O逆时针旋转得到，旋转角为（），连接、，求的最小值．
18．（2022·广东·九年级专题练习）如图1，已知正方形ABCD，AB＝4，以顶点B为直角顶点的等腰Rt△BEF绕点B旋转，BE＝BF＝，连接AE，CF．
(1)求证：△ABE≌△CBF．
(2)如图2，连接DE，当DE＝BE时，求S△BCF的值．（S△BCF表示△BCF的面积）
(3)如图3，当Rt△BEF旋转到正方形ABCD外部，且线段AE与线段CF存在交点G时，若M是CD的中点，P是线段DG上的一个动点，当满足MP+PG的值最小时，求MP的值．
19．（2021·四川·达州市第一中学校九年级期中）如图，矩形的顶点、分别在、轴的正半轴上，点的坐标为，一次函数的图象与边、、轴分别交于点、、，，并且满足，点是线段上的一个动点．
（1）求的值；
（2）连接，若的面积与四边形的面积之比为，求点的坐标；
（3）求的最小值．
20．（2022·全国·九年级）已知抛物线y＝ax2＋bx＋c与x轴交于A（﹣1，0），B（5，0）两点，C为抛物线的顶点，抛物线的对称轴交x轴于点D，连接BC，且tan∠CBD，如图所示．
（1）求抛物线的解析式；
（2）设P是抛物线的对称轴上的一个动点．
①过点P作x轴的平行线交线段BC于点E，过点E作EF⊥PE交抛物线于点F，连接FB、FC，求△BCF的面积的最大值；
②连接PB，求PC＋PB的最小值．
21．（2019·四川绵阳·中考真题）在平面直角坐标系中，将二次函数的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与轴交于点、(点在点的左侧)，，经过点的一次函数的图象与轴正半轴交于点，且与抛物线的另一个交点为，的面积为5．
(1)求抛物线和一次函数的解析式；
(2)抛物线上的动点在一次函数的图象下方，求面积的最大值，并求出此时点E的坐标；
(3)若点为轴上任意一点，在(2)的结论下，求的最小值．
22．（2019·湖南张家界·中考真题）已知抛物线过点，两点，与y轴交于点C，．
(1)求抛物线的解析式及顶点D的坐标；
(2)过点A作，垂足为M，求证：四边形ADBM为正方形；
(3)点P为抛物线在直线BC下方图形上的一动点，当面积最大时，求点P的坐标；
(4)若点Q为线段OC上的一动点，问：是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．
23．（2019·重庆·中考真题）如图，在平面在角坐标系中，抛物线y=x2-2x-3与x轴交于点A，B（点A在点B的左侧）交y轴于点C，点D为抛物线的顶点，对称轴与x轴交于点E．
（1）连结BD，点M是线段BD上一动点（点M不与端点B，D重合），过点M作MN⊥BD交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为H，交BD于点F，点P是线段OC上一动点，当MN取得最大值时，求HF+FP+PC的最小值；
（2）在（1）中，当MN取得最大值HF+FP+1/3PC取得小值时，把点P向上平移个单位得到点Q，连结AQ，把△AOQ绕点O瓶时针旋转一定的角度（0°