（寒假）沪教版数学九年级重难点讲练测重难点05两种数学思想方法（2份，原卷版+解析版）

这是一份（寒假）沪教版数学九年级重难点讲练测重难点05两种数学思想方法（2份，原卷版+解析版），文件包含寒假沪教版数学九年级重难点讲练测重难点05两种数学思想方法原卷版doc、寒假沪教版数学九年级重难点讲练测重难点05两种数学思想方法解析版doc等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。
考点一：分类讨论思想
考点二：数形结合思想
【考点剖析】
考点一：分类讨论思想
一．填空题（共4小题）
1．（2022•奉贤区二模）如图，在等边△ABC中，AB＝2，如果以BC为直径的⊙D和以A为圆心的⊙A相切，那么⊙A的半径r的值是 ．
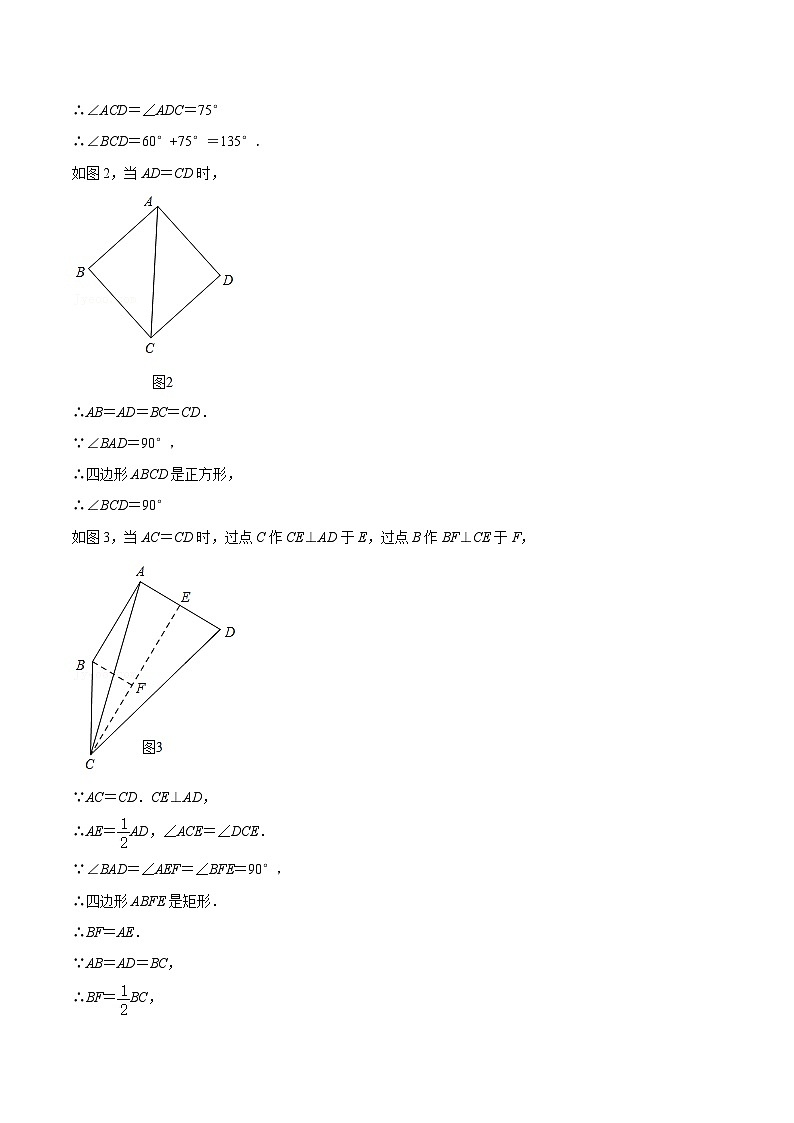
2．（2022春•徐汇区期末）定义：如果一个凸四边形的一条对角线把四边形分成两个等腰三角形，那么称这个凸四边形为“等腰四边形”，把这条对角线称为“界线”，已知在“等腰四边形”ABCD中，AB＝BC＝AD，∠BAD＝90°，且AC为界线，则∠BCD的度数为 ．
3．（2022春•静安区校级期中）如图，线段AB两点的坐标分别为A（﹣4，0）、B（﹣2，﹣4），在x轴的下方存在点C，使以点A，B，C为顶点的三角形与△ABO全等，则点C的坐标为 ．
4．（2020秋•普陀区期末）在Rt△ABC中，∠C＝90°，AC＝6，点D为边BC上一点，将△ACD沿直线AD翻折得到△AED，点C的对应点为点E，联结BE，如果△BDE是以BD为直角边的等腰直角三角形，那么BC的长等于 ．
二．解答题（共3小题）
5．（2022春•长宁区校级期末）如图矩形ABCD中，AB＝2，AD＝4，点P是边AD上一点，联结BP，过点P作PE⊥BP，交DC于E点，将△ABP沿直线PE翻折，点B落在点B′处，若△B′PD为等腰三角形，求AP的长．
6．（2022•松江区校级模拟）如图1，点C是半圆AB上一点（不与A、B重合），OD⊥BC交弧BC于点D，交弦BC于点E，连接AD交BC于点F．
（1）如图1，如果AD＝BC，求∠ABC的大小；
（2）如图2，如果AF：DF＝3：2，求∠ABC的正弦值；
（3）连接OF，⊙O的直径为4，如果△DFO是等腰三角形，求AD的长．
7．（2022春•金山区月考）已知：△ABC内接于半径为2的⊙O，BC＝，射线BO交边AC于点E．
（1）如果点E恰好是边AC的中点，求边AB的长；
（2）如果△ABE∽△ACB，求∠ABC的大小；
（3）当△AEO为等腰三角形时，求∠ABC的大小．
考点二：数形结合思想
一．选择题（共2小题）
1．（2022•青浦区模拟）如图，在平行四边形ABCD中，延长BC至点E，使CE＝2BC，联结DE，设＝，＝，那么可表示为（ ）
A．+2B．﹣2C．﹣+2D．﹣﹣2
2．（2022•松江区校级模拟）如图，已知△ABC，AD为三角形ABC的中线，，，则＝（ ）
A．B．C．D．
二．填空题（共6小题）
3．（2022春•浦东新区校级期中）已知OA，OB，OM均是⊙O的半径，OA⊥OB，＝．如果+＝k，那么k的值是 ．
4．（2022•奉贤区二模）在梯形ABCD中，AB∥CD，AB＝2CD，E是腰BC的中点，联结AE．如果设＝，＝，那么＝ （含、的式子表示）．
5．（2022•宝山区二模）如图，已知AC、BD是梯形ABCD的对角线，AD∥BC，BC＝2AD，如果设＝，＝，那么向量用向量、表示为 ．
6．（2022•松江区校级模拟）如图，已知在△ABC中，AB＝AC，，将△ABC翻折，使点C与点A重合，折痕DE交边BC于点D，交边AC于点E，那么的值为 ．
7．（2022春•普陀区校级期中）如图，已知在Rt△ABC中，两条直角边AC＝6，BC＝8，将Rt△ABC绕着点C顺时针旋转，其中AB的对应点分别记为点A′和点B′，当A′B′与边BC的交点E恰好是A′B′的中点时，则AA′的长为 ．
8．（2022春•金山区月考）如图，已知AC、BD是平行四边形ABCD的对角线．设向量＝，向量＝，那么向量可以表示为 （用向量、表示）．
三．解答题（共5小题）
9．（2022秋•奉贤区月考）如图，已知平行四边形ABCD，BC＝2AB，点E在边BC上，AE平分∠BAD．
（1）写出与相等的向量是 ；
（2）求作：（要求保留作图痕迹）；
（3）联结DE，如果，那么|+|＝ ．
10．（2021秋•普陀区期末）如图，在平面直角坐标系xOy中，已知抛物线y＝x2+bx+c与直线y＝﹣x+1交于点A（m，0），B（﹣3，n），与y轴交于点C，联结AC．
（1）求m、n的值和抛物线的表达式；
（2）点D在抛物线y＝x2+bx+c的对称轴上，当∠ACD＝90°时，求点D的坐标；
（3）将△AOC平移，平移后点A仍在抛物线上，记作点P，此时点C恰好落在直线AB上，求点P的坐标．
11．（2021秋•松江区期末）如图，已知直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过A、B两点．
（1）求这条抛物线的表达式；
（2）直线x＝t与该抛物线交于点C，与线段AB交于点D（点D与点A、B不重合），与x轴交于点E，联结AC、BC．
①当＝时，求t的值；
②当CD平分∠ACB时，求△ABC的面积．
12．（2022秋•黄浦区月考）如图，在△ABC中AB＝AC＝4，cs∠B＝，点D是边BA延长线上过的点，点E是边BC上一点（不与端点重合），联结DE交AC于点F，联结DC，且DE＝DC，设AD＝x，EC＝y．
（1）求证：；
（2）求y关于x的函数关系式及其定义域；
（3）联结AE，当△AEF与△DFC相似时，求AD的长．
13．（2022秋•徐汇区校级期中）已知矩形ABCD中，AB＝6，BC＝8，P是边AD上一点，将△ABP沿直线PB翻折，使点A落在点E处，联结DE，直线DE与射线CB相交于点F．
（1）如图1，当F在边BC上，若PD＝BF时，求AP的长；
（2）若射线AE交BC的延长线于Q，设AP＝x，QC＝y，求y与x的函数解析式，并写出x的取值范围；
（3）①如图2，直线DE与边AB相交于点G，若△PDE与△BEG相似，求∠AEG的度数；
②如图3，当直线DE与BP的延长线相交于点H时，若S△PDH＝S△BEP．求DH的长．