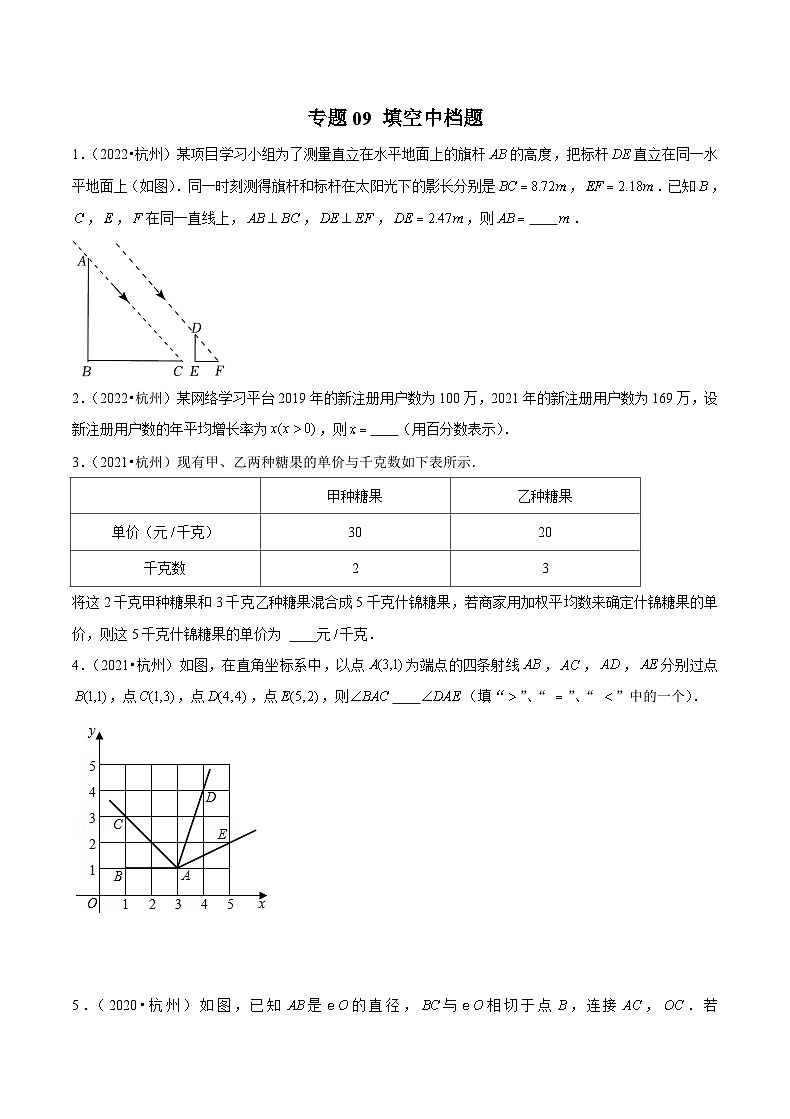




所属成套资源:(杭州专用)中考数学二轮复习模拟题分类汇编 (2份,原卷版+解析版)
(杭州专用)中考数学二轮复习模拟题分类汇编专题09 填空中档题(2份,原卷版+解析版)
展开
这是一份(杭州专用)中考数学二轮复习模拟题分类汇编专题09 填空中档题(2份,原卷版+解析版),文件包含杭州专用中考数学二轮复习模拟题分类汇编专题09填空中档题原卷版doc、杭州专用中考数学二轮复习模拟题分类汇编专题09填空中档题解析版doc等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
【答案】9.88
【详解】同一时刻测得旗杆和标杆在太阳光下的影长分别是,.
,
,
,,
,
△,
,即,
解得,
旗杆的高度为.
故答案为:9.88.
2.(2022•杭州)某网络学习平台2019年的新注册用户数为100万,2021年的新注册用户数为169万,设新注册用户数的年平均增长率为,则 (用百分数表示).
【答案】
【详解】新注册用户数的年平均增长率为,
依题意得:,
解得:,(不合题意,舍去).
,
新注册用户数的年平均增长率为.
故答案为:.
3.(2021•杭州)现有甲、乙两种糖果的单价与千克数如下表所示.
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为 元千克.
【答案】24【详解】这5千克什锦糖果的单价为:(元千克).
故答案为:24.
4.(2021•杭州)如图,在直角坐标系中,以点为端点的四条射线,,,分别过点,点,点,点,则 (填“”、“ ”、“ ”中的一个).
【答案】
【详解】连接,
由上图可知,,
是等腰直角三角形,
,
又,
同理可得,
,
则在中,有,
是等腰直角三角形,
,
,
故答案为:.
5.(2020•杭州)如图,已知是的直径,与相切于点,连接,.若,则 .
【答案】
【详解】是的直径,与相切于点,
,
,
,
设,,
,
,
,
故答案为:.
6.(2020•杭州)一个仅装有球的不透明布袋里共有4个球(只有编号不同),编号分别为1,2,3,5.从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是 .
【答案】
【详解】根据题意画图如下:
共有16种等情况数,其中两次摸出的球的编号之和为偶数的有10种,
则两次摸出的球的编号之和为偶数的概率是.
故答案为:.
7.(2019•杭州)在直角三角形中,若,则 .
【答案】或
【详解】若,设,则,所以,所以;
若,设,则,所以,所以;
综上所述,的值为或.
故答案为或.
8.(2019•杭州)某函数满足当自变量时,函数值,当自变量时,函数值,写出一个满足条件的函数表达式 .
【答案】(答案不唯一)
【详解】设该函数的解析式为,
函数满足当自变量时,函数值,当自变量时,函数值,
解得:,
所以函数的解析式为,
故答案为:(答案不唯一).
9.(2018•杭州)如图,是的直径,点是半径的中点,过点作,交于,两点,过点作直径,连接,则 .
【答案】
【详解】点是半径的中点,
,
,
,
,
,
故答案为:.
10.(2018•杭州)某日上午,甲,乙两车先后从地出发沿同一条公路匀速前往地,甲车8点出发,如图是其行驶路程(千米)随行驶时间(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度(单位:千米小时)的范围是 .
【答案】
【详解】根据图象可得,甲车的速度为(千米时).
由题意,得,
解得.
故答案为:.
11.(2022•上城区一模)如图为《北京2022年冬残奥会会徽》纪念邮票,其规格为边长14.92毫米的正八边形,则正八边形的内角和为 .
【答案】
【详解】.
故答案为:.
12.(2022•上城区一模)如图1,把标准纸(长与宽之比为一次又一次对开,按图2叠放,可以发现,这些叠放起来的矩形的右上顶点与左下顶点在同一直线上.若以图2最大矩形的左下顶点为原点,以宽和长所在直线分别为轴和轴,则这组矩形的右上顶点所在直线的函数表达式为 .
【答案】
【详解】设标准纸的宽为1,长为,
则第一次对开后,的坐标为,,第二次对开后,的坐标为,,
这些叠放起来的矩形的右上顶点与左下顶点在同一直线上,
设这条直线的解析式为,
把、的坐标代入得,
解得,
直线的函数表达式为.
故答案为:.
13.(2022•拱墅区一模)如图是一个可以自由转动的两色转盘,其中白色扇形和红色扇形的圆心角分别为和.若让转盘自由转动一次,则指针落在白色区域的概率是 .若让转盘自由转动两次,则指针一次落在白色区域,另一次落在红色区域的概率是 .
【答案】,
【详解】由图得:白色扇形的圆心角为,
故若让转盘自由转动一次,则指针落在白色区域的概率是:,
则转动一次,指针落在红色区域的概率是:,
故若让转盘自由转动两次,则指针一次落在白色区域,另一次落在红色区域的概率是:.
故答案为:,.
14.(2022•拱墅区一模)如图,是的直径,点是延长线上的一点,是的切线,为切点.若,.则 .
【答案】
【详解】连接,
是的切线,
,
在中,,
则,
,
,,
,
故答案为:.
15.(2022•西湖区一模)直角坐标系中的四个点:,,,,则 (填“”、“ ”、“ ”中的一个).
【答案】
【详解】,,,,
,,,,,,
,
,
,
故答案为:.
16.(2022•西湖区一模)如图,点,分别表示数,,则的取值范围为 .
【答案】
【详解】由题意得,,
解得.
故答案为:.
17.(2022•钱塘区一模)在中,.若,则 .
【答案】
【详解】,
,
在中,.
设,则,由勾股定理得,
,
,
故答案为:.
18.(2022•钱塘区一模)已知点是外一点,,分别与相切于点,,连结,.若的半径为3,劣弧的长为,则的度数为 .
【答案】
【详解】设劣弧所对的圆心角度数为,
根据题意可得:,
,
,是的切线,
,
.
故答案为.
19.(2022•淳安县一模)如图,的半径是3,点是弦延长线上的一点,连接,若,,则弦的长为 .
【答案】
【详解】
连接,过作于,
则,
,,
,
在中,由勾股定理得:,
,过,
,
故答案为:.
20.(2022•淳安县一模)如图,在每个小正方形边长都为1的网格中,有四个点,,,,以其中任意三点为顶点的三角形的外接圆半径长是 .
【答案】
【详解】连接,,作,的垂直平分线,两直线相交于,
则为的外接圆的圆心,为外接圆的半径,
由勾股定理得,
故答案为:.
21.(2022•富阳区一模)甲、乙、丙、丁四人围坐在一张方桌周围(共四个座位),甲、乙两人坐在相对位置的概率是 .
【答案】
【详解】画树状图如图:
共有12种等可能的结果,其中甲、乙两人坐在相对位置的结果有4种,
甲、乙两人坐在相对位置的概率为:,
故答案为:.
22.(2022•富阳区一模)商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价,最高销售限价以及常数确定实际销售价格为,这里的被称为乐观系数.经验表明,最佳乐观系数恰好使得,据此可得,最佳乐观系数的值等于 .
【答案】
【详解】,,,
,
,
解得,
,
.
故答案为:.
23.(2022•临安区一模)在等腰中,,,以边的中点为圆心长为半径画圆,该圆分别交,边于点,,是圆上一动点(与点,不重合),连接,,则 .
【答案】或
【详解】连接,,
,,
,
,
,
,
,
当点在优弧上时,,
当点在劣弧上时,,
或,
故答案为:或.
24.(2022•临安区一模)杭州市将在2022年举办亚运会,为加强学校体育工作,某学校决定购买一批篮球和足球共100个.已知篮球和足球的单价分别为120元和90元.根据需求,篮球购买的数量不少于40个.学校可用于购买这批篮球和足球的资金最多为10260元,则有 种购买方案.
【答案】3
【详解】设购买篮球个,则购买足球个,
依题意得:,
解得:.
又为正整数,
可以为40,41,42,
共有3种购买方案.
故答案为:3.
25.(2022•钱塘区二模)如图,点在轴正半轴上,点在第一象限,,函数的图象分别交,于点,,若,,则的长为 ;当时,的值为 .
【答案】5;
【详解】如图,过点作于,过点作于,过点作于点,设,
,.
,
,
,
,
.
设,
,,
,,
,,
反比例函数的图象分别交边,于点,,
,解得,
,,
.
,
,即,
.
若,则.
由射影定理可得.
,即,
在中,由勾股定理可得,,
,
整理得.
.
故答案为:5;.
26.(2022•钱塘区二模)如图,在中,点、分别为、的中点,,已知,,则的周长为 .
【答案】
【详解】如图,连接、过点作交的延长线于点,
四边形为平行四边形,
,,,
四边形为平行四边形,
,
,
四边形为矩形,
,,,
、分别为、的中点,
,
,
,
,
,
,
,
,
.
故答案为:.
27.(2022•西湖区校级一模)已知,的直径,弦,,垂足为,则的长为 .
【答案】8或2
【详解】①连接,如图所示:
的直径,
,
弦,,
,
在中,由勾股定理得:,
;
②连接,如图所示:
同①得:,
;
综上所述,的长为8或2,
故答案为:8或2.
28.(2022•西湖区校级一模)如图,在中,,,则图中阴影部分的面积为 .
【答案】
【详解】,
,
.
故答案为:.
29.(2022•萧山区校级一模)如图,在中,,,,则的长为 .
【答案】
【详解】过点作,垂足为,
在中,,,
,
在中,,
,
,
故答案为:.
30.(2022•萧山区校级一模)已知反比例函数的表达式为,,和,是反比例函数图象上两点,若时,,则的取值范围是 .
【答案】
【详解】反比例函数的图象上两点,,,,当时,有,
,
解得,
故答案为:.
31.(2022•萧山区一模)已知圆锥的底面半径为3,侧面积为,则这个圆锥的高为 .
【答案】4
【详解】设圆锥的母线长为,则,解得,
圆锥的高.
32.(2022•萧山区一模)已知,,,是一次函数图象上不同的两点.
(1)若,则 ;
(2)若,则的取值范围是 .
【答案】1,
【详解】(1),,,是一次函数图象上不同的两点,
,
,
故答案为:1.
(2),
,
.
故答案为:.
33.(2022•滨江区一模)在中,,,以为圆心,以长为半径画弧,交边于点,连接,则 度.
【答案】36
【详解】,,
,
,
.
故答案为:36.
34.(2022•滨江区一模)有两辆车按1,2编号,洪、杨两位老师可任意选坐一辆车,则两位老师同坐2号车的概率为 .
【答案】
【详解】画树状图为:
共有4种等可能的结果,其中两位老师同坐2号车的结果数为1,
所以两位老师同坐2号车的概率.
故答案为:.
35.(2022•上城区二模)已知方程有两个实数根,则所取的值可以是 .(填一个即可)
【答案】2(答案不唯一)
【详解】一元二次方程有两个实数根,
△,
解得,
取.
故答案为:2(答案不唯一).
36.(2022•上城区二模)已知点和点为平面直角坐标系内两点,且点的坐标为,将点向右平移3个单位至点,则线段上任意一点的坐标可表示为 .
【答案】
【详解】如图,点,,
故答案为:,.
37.(2022•余杭区一模)如图,已知,若,,则的度数为 .
【答案】
【详解】,,是的外角,
,
,
.
故答案为:.
38.(2022•余杭区一模)定义新运算:对于任意实数,,都有,例如.若关于的函数的图象与轴仅有一个公共点,则实数的值为 .
【答案】0或
【详解】根据新定义得,
⊕,
即,
当时,函数为,与轴仅有一个公共点,符合题意;
当时,函数为二次函数,其图象与轴仅有一个公共点,则:
△,
解得,
综上所述,或,
故答案为:0或.
39.(2022•富阳区二模)如图,正方形的边长为8,以点为圆心,长为半径画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面半径是 .
【答案】1
【详解】设圆锥的底面圆的半径为,
根据题意可知:
,,
底面圆的周长等于弧长:
,
解得.
答:该圆锥的底面圆的半径是1.
故答案为:1.
40.(2022•富阳区二模)如图,直线经过点,,两点,则不等式组的解集为 .
【答案】
【详解】当时,,
直线与直线交于点,
根据图象可知,不等式组的解集为,
故答案为:.
41.(2022•西湖区校级模拟)如图,是的直径,是的切线,为切点.若,,则的长为 .
【答案】6
【详解】是的直径,是的切线,
,
,
,
.
故答案为:6.
42.(2022•西湖区校级模拟)如图,已知、,为第四象限内一点且,若,则 .
【答案】
【详解】如图,过点作轴,
,
,
、,
轴,
,
,,
.
故答案为:.
43.(2022•富阳区一模)如图,线段是的直径,弦,垂足为,点是上任意一点,,,则的值为 .
【答案】
【详解】连接,
线段是的直径,弦,,,
在中,设为,可得:,
解得:,
,
,
,
故答案为:.
44.(2022•富阳区一模)已知二次函数的图象经过、、,则 (选择“”“ ”“ ”填空).
【答案】
【详解】
整理得:,
故答案为:.
45.(2022•西湖区校级二模)如图,在中,,是边上的中线,在上取一点,连结,使得,若,则 .
【答案】
【详解】设,则,
,
,
,是边上的中线,
,,
,
,
解得:,
,
故答案为:.
46.(2022•西湖区校级二模)已知点,在反比例函数的图象上,且.则的取值范围为 .
【答案】
【详解】由可知图象位于一、三象限,随的增大而减小.
点,在反比例函数的图象上,且.
点、不在同一象限,则点在第一象限,点在第三象限.
,解得.
故答案为:.
47.(2022•西湖区校级模拟)每天登录“学习强国” 进行学习,在获得积分的同时,还可获得“点点通”收入奖励,李老师最近一周每日“点点通”收入明细如表:
则这组数据的众数是 ,中位数是 .
【答案】21,21
【详解】将这7个数据从小到大排列为:15,21,21,21,27,27,30,
所以中位数为21,众数为21,
故答案为:21,21.
48.(2022•西湖区校级模拟)如图,表示垂直于地面的两根电线杆的主视图,线段和线段表示两根电线杆,线段和表示两根拉紧的铁丝,和交于点.测量得米,点距地面的高度为3米,则的长为 米.
【答案】12
【详解】过点作于,
由题意得、也分别垂直于,
,
,
,
,即,
,
,
,
,即,
,
的长为12米.
故答案为:12.
49.(2022•下城区校级二模)某路口红绿灯的时间设置为:红灯30秒,绿灯27秒,黄灯3秒.当人或车随意经过该路口时,遇到红灯的概率是 .
【答案】
【详解】遇到红灯的概率为:,
故答案为:.
50.(2022•下城区校级二模)如图,已知是的直径,为外延长线上一点,切于.若,,则的值为 .
【答案】
【详解】,,
,
,
,
切于,
,
在中,由勾股定理得:,
故答案为:.
51.(2022•杭州模拟)如图,四边形是的内接四边形,的半径为4,的长为,则的大小是 .
【答案】
【详解】连接,,设,
的半径为4,的长为,
,
解得:,
即,
,
故答案为:.
52.(2022•杭州模拟)如图所示的电路中,当随机闭合开关、、中的两个时,能够让灯泡发光的概率为 .
【答案】
【详解】因为随机闭合开关,,中的两个,有3种方法,其中有2种能够让灯泡发光
所以(灯泡发光).
故本题答案为:.
53.(2022•江干区校级模拟)圆柱的侧面展开图是一个相邻的两边长分别为4,的长方形,则圆柱体的体积为 .
【答案】或8
【详解】①以为底面周长,4为高,
此时圆柱体的底面半径为,
圆柱体的体积为,
②以4为圆柱体的底面周长,为高,
此时圆柱体的底面半径为,
圆柱体的体积为,
故答案为:或8.
54.(2022•江干区校级模拟)如图,在中,弦,点在上移动,连接,过点作交于点,则的最大值为 .
【答案】
【详解】连接,如图,
,
,
,
当的值最小时,的值最大,
而时,最小,此时、两点重合,
,
即的最大值为,
故答案为:.
55.(2022•拱墅区模拟)无盖圆柱形杯子的展开图如图所示.将一根长为的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 .
【答案】5
【详解】由题意可得:
杯子内的筷子长度为:,
则筷子露在杯子外面的筷子长度为:.
故答案为:5.
56.(2022•拱墅区模拟)、两地相距,甲乙两人沿同一条路线从地到地,甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达,甲、乙两人离开地的距离与时间的关系如图所示,则乙出发 小时后追上甲.
【答案】
【详解】乙提高后的速度为:,
由图象可得:;
,
由方程组,
解得,
(小时),
即乙出发小时后和甲相遇.
故答案为:.甲种糖果
乙种糖果
单价(元千克)
30
20
千克数
2
3
星期
一
二
三
四
五
六
日
收入
15
21
27
27
21
30
21
相关试卷
这是一份(杭州专用)中考数学二轮复习模拟题分类汇编专题06 选择压轴题(2份,原卷版+解析版),文件包含杭州专用中考数学二轮复习模拟题分类汇编专题06选择压轴题原卷版doc、杭州专用中考数学二轮复习模拟题分类汇编专题06选择压轴题解析版doc等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
这是一份(杭州专用)中考数学二轮复习模拟题分类汇编专题05 选择中档题二(2份,原卷版+解析版),文件包含杭州专用中考数学二轮复习模拟题分类汇编专题05选择中档题二原卷版doc、杭州专用中考数学二轮复习模拟题分类汇编专题05选择中档题二解析版doc等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
这是一份(杭州专用)中考数学二轮复习模拟题分类汇编专题04 选择中档题一(2份,原卷版+解析版),文件包含杭州专用中考数学二轮复习模拟题分类汇编专题04选择中档题一原卷版doc、杭州专用中考数学二轮复习模拟题分类汇编专题04选择中档题一解析版doc等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。









