山东省临沂市罗庄区2024-2025学年九年级上学期期中考试数学试题（原卷版）-A4

这是一份山东省临沂市罗庄区2024-2025学年九年级上学期期中考试数学试题（原卷版）-A4，共7页。
（时间：120分钟；总分120分）
注意事项：
1．答题前，请先认真浏览试卷；然后按要求操作；
2．答题时，要端正心态，仔细思考，认真书写，规范作图，保持卷面整洁！
一、选择题（本大题共10小题，每小题3分，共30分）
1. 我国传统文化中的“福禄寿喜”，这四个图案中既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
2. 已知二次函数的对称轴为直线，则的值是（ ）
A. 4B. 3C. 2D. 1
3. 关于的一元二次方程的两实数根互为相反数，则的值为（ ）
A. B. 0C. 1D. 或0
4. 如图，在中，，将绕点B逆时针旋转得到，点，的对应点分别为，，当点恰好落在边上时，连接，下列结论一定正确的是（ ）

A. B. C. D.
5. 一个边长为的正多边形的内角和是其外角和的倍，则这个正多边形的外接圆半径是（ ）
A. B. 3C. 1D. 21
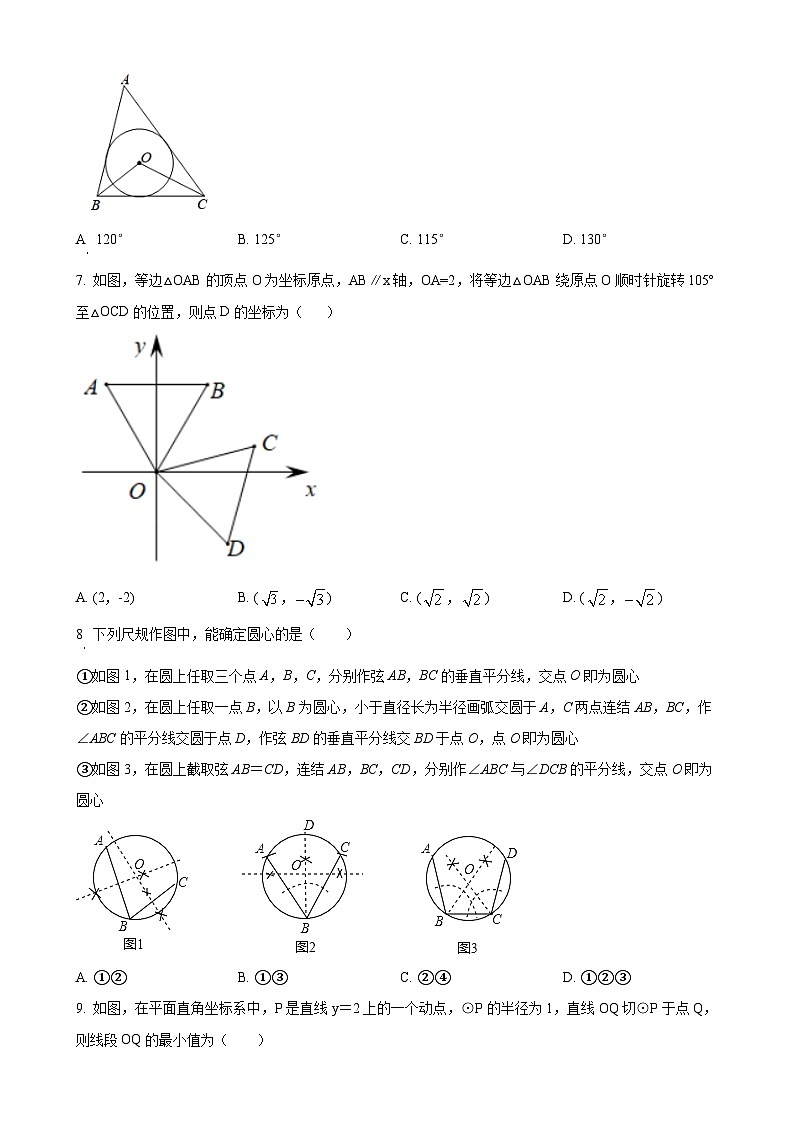
6. 如图，点O为△ABC的内心，∠A＝50°，则∠BOC的度数为（ ）
A 120°B. 125°C. 115°D. 130°
7. 如图，等边△OAB的顶点O为坐标原点，AB∥x轴，OA=2，将等边△OAB绕原点O顺时针旋转105º至△OCD的位置，则点D的坐标为（ ）
A. (2，-2)B. (，)C. (，)D. (，)
8 下列尺规作图中，能确定圆心的是（ ）
①如图1，在圆上任取三个点A，B，C，分别作弦AB，BC的垂直平分线，交点O即为圆心
②如图2，在圆上任取一点B，以B为圆心，小于直径长为半径画弧交圆于A，C两点连结AB，BC，作∠ABC的平分线交圆于点D，作弦BD的垂直平分线交BD于点O，点O即为圆心
③如图3，在圆上截取弦AB＝CD，连结AB，BC，CD，分别作∠ABC与∠DCB的平分线，交点O即为圆心
A. ①②B. ①③C. ②④D. ①②③
9. 如图，在平面直角坐标系中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ的最小值为（ ）
A. 1B. 2C. D.
10. 如图，在的正方形网格中，动点同时从两点匀速出发，以每秒1个单位长度的速度沿网格线运动至格点停止．动点的运动路线为：；动点的运动路线为：，连接．设动点运动时间为的面积为．则与之间的函数关系用图象表示大致是（ ）
A B.
C. D.
二、填空题（本题共6小题，每小题3分，共18分）
11. 为了美化环境，某市加大绿化投资，2015年用于绿化投资300万元，2017年用于绿化投资363万元，则这两年绿化投资的年均增长率为_____．
12. 年9月日，大型客机取得中国民用航空局型号合格证，这标志着我国具备按照国际通行适航标准研制大型客机的能力，是我国大飞机事业征程上的重要里程碑．如果某型号飞机降落后滑行的距离s（单位：米）关于滑行的时间t（单位：秒）的函数解析式是，则该飞机着陆后滑行最长时间为______秒．
13. 已知在圆内接三角形中，，圆心O到的距离为，圆的半径为，则腰的长为____________．
14. 如图，扇形中，，点C为中点，交弧于点E，以点O为圆心，的长为半径作弧交于点D．若，则阴影部分面积为__．
15. 如图，抛物线的对称轴为直线，与轴的一个交点坐标为，其部分图象如图，下列结论：①；②方程的两个根是，；③；④当时，的取值范围是；⑤当时，随增大而增大．其中正确结论的序号是________．
16. 阅读理解：设，，若，则，即，已知，，且，则的值为______．
三、解答题（本题共7小题，共72分．解答应写出文字说明、证明过程或演算步骤．）
17. 解一元二次方程：
（1）；
（2）．
18. 如图，的顶点坐标分别为．
（1）画出与关于轴对称的图形，并写出的坐标；
（2）画出绕原点逆时针旋转的，并写出点的坐标．
19. 根据以下素材，完成探索任务．
20. 如图，四边形ABCD内接于⊙O，∠BAD=90°，AD、BC的延长线交于点F，点E在CF上，且∠DEC=∠BAC．
（1）求证：DE是⊙O的切线；
（2）若AB=AC，CE=10，EF=14，求CD．
21. 如图1所示的某种发石车是古代一种远程攻击的武器，发射出去的石块的运动轨迹是抛物线的一部分，且距离发射点20米时达到最大高度10米．将发石车置于山坡底部O处，山坡上有一点A，点A与点O的水平距离为30米，与地面的竖直距离为3米，AB是高度为3米的防御墙．若以点O为原点，建立如图2所示的平面直角坐标系．
（1）求石块运动轨迹所在抛物线的解析式；
（2）试通过计算说明石块能否飞越防御墙AB；
（3）在竖直方向上，试求石块飞行时与坡面OA的最大距离．
22. 如图1，在Rt△ABC中，∠C＝90°，AC＝BC，点D，E分别在边AC，BC上，CD＝CE，连接AE，点F，H，G分别为DE，AE，AB的中点连接FH，HG
（1）观察猜想图1中，线段FH与GH的数量关系是 ，位置关系是
（2）探究证明：把△CDE绕点C顺时针方向旋转到图2位置，连接AD，AE，BE判断△FHG的形状，并说明理由
（3）拓展延伸：把△CDE绕点C在平面内自由旋转，若CD＝4，AC＝8，请直接写出△FHG面积的最大值
23. 已知抛物线（为常数）经过点．
（1）求该抛物线的函数表达式．
（2）已知点在该抛物线上．
（ⅰ）当时，比较的大小；
探索果园土地规划和销售利润问题
素材1
某农户承包了一块长方形果园，图1是果园的平面图，其中米，米．准备在它的四周铺设道路，上下两条横向道路的宽度都为米，左右两条纵向道路的宽度都为米，中间部分种植水果．已知道路的路面造价是每平方米50元；出于货车通行等因素的考虑，横向道路宽度不超过24米，且不小于10米．
素材2
该农户发现某一种草莓销售前景比较不错，经市场调查，草莓培育一年可产果，已知每平方米的草莓销售平均利润为100元；果园每年的承包费为25万元，期间需一次性投入33万元购进新苗，每年还需25万元的养护、施肥、运输等其余费用．
问题解决
任务1
解决果园中路面宽度的设计对种植面积的影响．
（1）请直接写出纵向道路宽度的取值范围．
（2）若中间种植的面积是44800平方米，则路面设置的宽度是否符合要求．
任务2
解决果园种植的预期利润问题．（净利润草莓销售的总利润路面造价费用果园承包费用新苗购置费用其余费用）
（3）经过1年后，农户是否可以达到预期净利润400万元？请说明理由．