第1周——2023学年人教版数学九年级下册周周测

这是一份第1周——2023学年人教版数学九年级下册周周测，共8页。试卷主要包含了下列关系式中，是反比例函数的是等内容，欢迎下载使用。
A.B.C.D.
2.已知反比例函数的解析式为，则a的取值范围是( )
A.B.C.D.
3.函数与在同一坐标系内的图象可能是( )
A.B.
C.D.
4.已知点在函数的图象上,则下列判断正确的是( )
A. B. C. D.
5.如图，函数与函数的图象相交于点，.若，则x的取值范围是( )
A.或B.或
C.或D.或
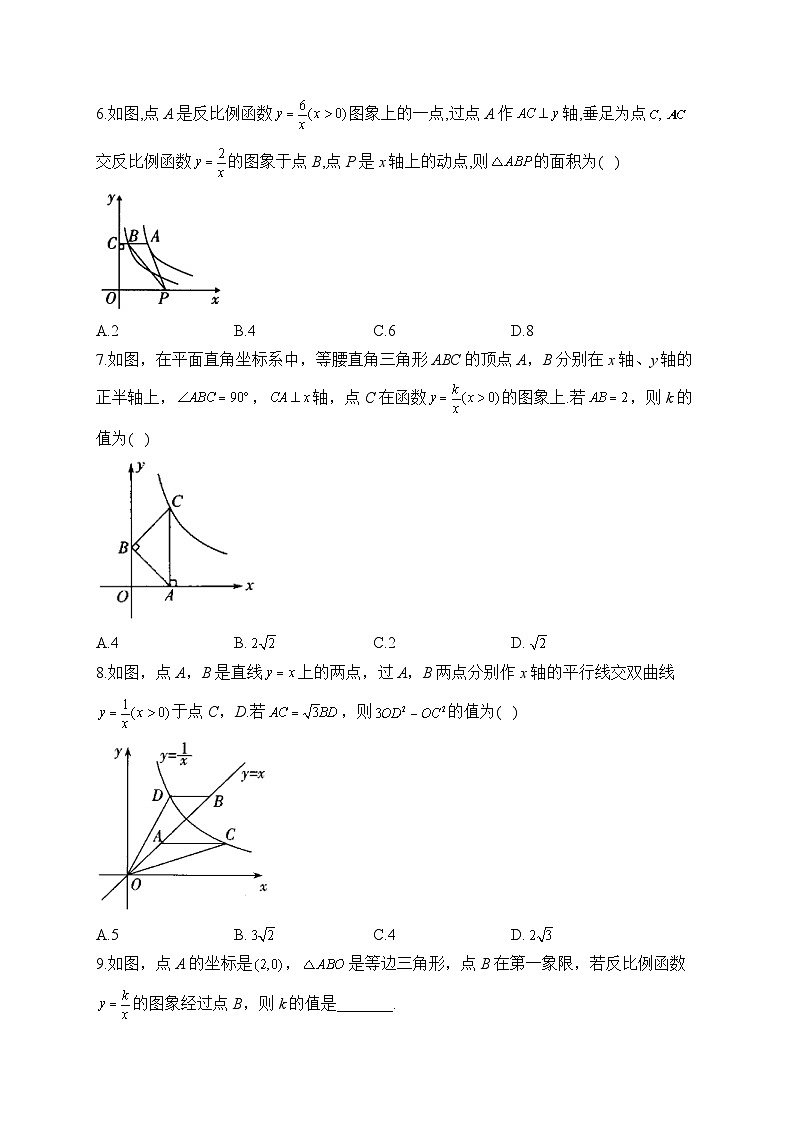
6.如图,点A是反比例函数图象上的一点,过点A作轴,垂足为点交反比例函数的图象于点B,点P是x轴上的动点,则的面积为( )
A.2B.4C.6D.8
7.如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A，B分别在x轴、y轴的正半轴上，，轴，点C在函数的图象上.若，则k的值为( )
A.4B.C.2D.
8.如图，点A，B是直线上的两点，过A，B两点分别作x轴的平行线交双曲线于点C，D.若，则的值为( )
A.5B.C.4D.
9.如图，点A的坐标是，是等边三角形，点B在第一象限，若反比例函数的图象经过点B，则k的值是_______.
10.反比例函数，在第一象限的图象如图，已知，过的图象上的任意一点A作x轴的平行线交的图象于点B，交y轴于点C，若，则的表达式是___________.
11.如图,一次函数的图象与反比例函数的图象在第一象限相交于点A,与x轴相交于点B,点C在y轴上,若,则点C的坐标为_________.
12.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度与时间之间的函数关系,其中线段表示恒温系统开启阶段,双曲线的一部分表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求这天的温度y与时间的函数解析式
(2)求恒温系统设定的恒定温度.
(3)若大棚内的温度低于10 ℃时,蔬菜会受到伤害.问:这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
答案以及解析
1.答案：D
解析：A、B两个选项中的关系式是一次函数关系式，
C选项的函数y是的反比例函数，而y不是x的反比例函数，
D选项可化为，故它是反比例函数关系式；
故选：D.
2.答案：C
解析：由题意，得，解得.
3.答案：B
解析：当时，过第一、三、四象限，反比例函数位于第一、三象限；当时，过第二、三、四象限，反比例函数位于第二、四象限.结合选项中图象知，选项B正确.
4.答案：C
解析：∵点在函数的图象上且,
∴图象经过第一、三象限,在各个象限内,y随x的增大而减小,
.
5.答案：D
解析：当直线在反比例函数图象之上时，所对应的x的取值范围为或，即时，x的取值范围是或.故选D.
6.答案：A
解析：如图,过点A作轴于点轴,轴.设点,.由k的几何意义,得,.
7.答案：A
解析：在中，，，，
，.
轴，，
，
是等腰直角三角形.
又，
由勾股定理，得.
点C的坐标为.
把点代入函数，得.
故选A.
8.答案：C
解析：设A，B的横坐标分别是a，b，点A，B为直线上的两点，A的坐标是，B的坐标是.过A，B两点分别作x轴的平行线交双曲线于点C，D，C的坐标是，D的坐标是.，，两边平方得，即..故选C.
9.答案：
解析：过点B作于C.
是等边三角形，，
，，点B的坐标是，
把代入中，得.
10.答案：
解析：设的表达式为，轴，，，，，，的表达式为.
11.答案：(0,2)
解析：如图,过点A作轴,轴,垂足分别为点.由得,点A的坐标为(2,1),即.在中,.在中,..设点C的坐标为,由已知求出B点坐标为(1,0),根据勾股定理得,解得,.
12.答案：(1)
(2)20
(3)10
解析：(1)设线段所在直线的解析式为.
将点(0,10),(2,14)代入解析式,得
解得
∴线段所在直线的解析式为,
∴点B的坐标为(5,20),
∴线段所在直线的解析式为.
设双曲线的解析式为.
将点代入,得,
解得.
∴双曲线解析式为，
与x的函数解析式为
(2)由(1)可知,恒温系统设定的恒定温度为20 ℃.
(3)把代入,得,
解得.
.
∴恒温系统最多可以关闭10 h,才能使蔬菜避免受到伤害.