北师大版（2024）第一章 丰富的图形世界1.2 展开与折叠练习

这是一份北师大版（2024）第一章 丰富的图形世界1.2 展开与折叠练习，共7页。试卷主要包含了正方体的表面展开图可能是，如图所示，正方体的展开图为等内容，欢迎下载使用。
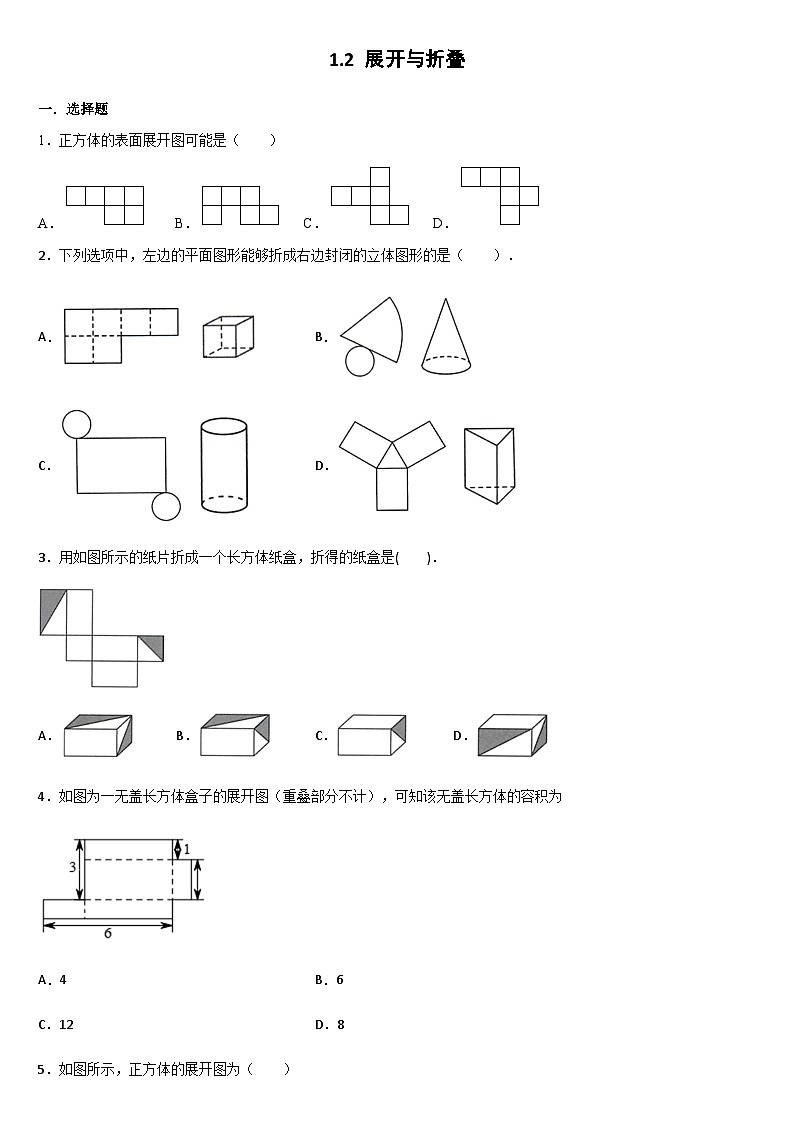
1．正方体的表面展开图可能是（ ）
A． B． C． D．
2．下列选项中，左边的平面图形能够折成右边封闭的立体图形的是（ ）．
A． B．
C． D．
3．用如图所示的纸片折成一个长方体纸盒，折得的纸盒是( )．
A．B．C．D．
4．如图为一无盖长方体盒子的展开图（重叠部分不计），可知该无盖长方体的容积为
A．4B．6
C．12D．8
5．如图所示，正方体的展开图为（ ）
A． B．
C． D．
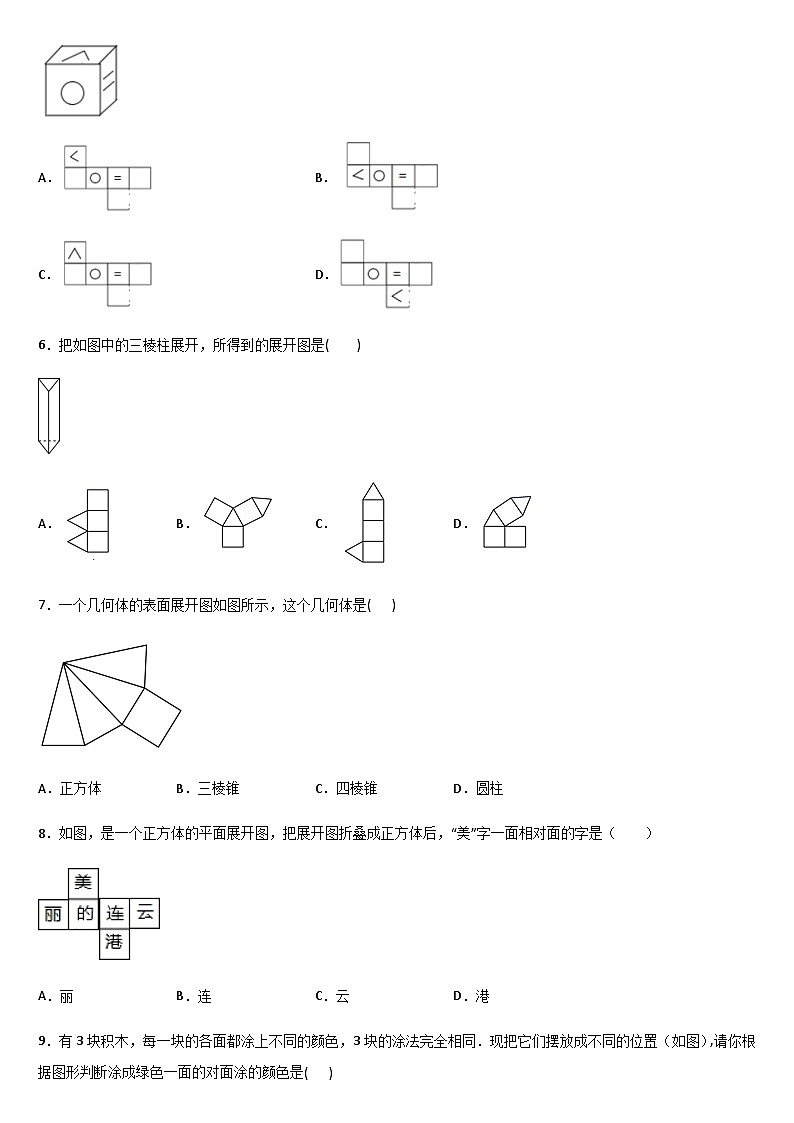
6．把如图中的三棱柱展开，所得到的展开图是( )
A．B．C．D．
7．一个几何体的表面展开图如图所示，这个几何体是( )
A．正方体B．三棱锥C．四棱锥D．圆柱
8．如图，是一个正方体的平面展开图，把展开图折叠成正方体后，“美”字一面相对面的字是（ ）
A．丽B．连C．云D．港
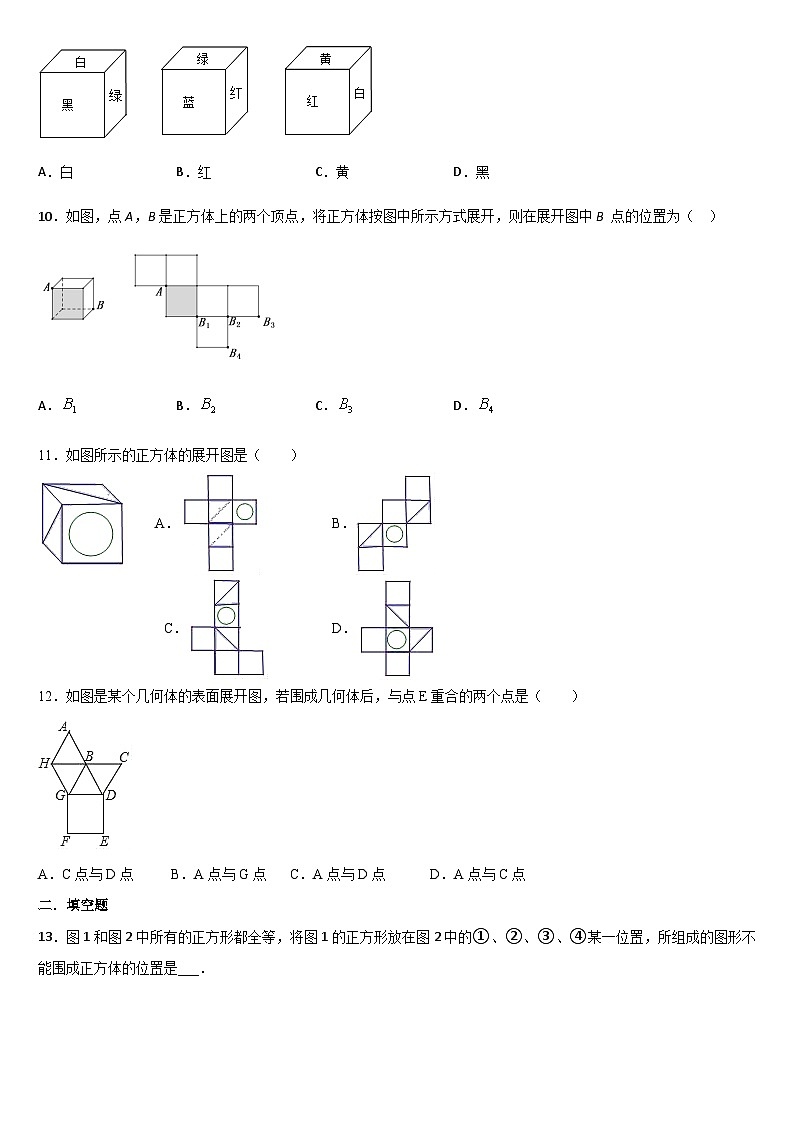
9．有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同．现把它们摆放成不同的位置（如图）,请你根据图形判断涂成绿色一面的对面涂的颜色是( )
A．白B．红C．黄D．黑
10．如图，点A，B是正方体上的两个顶点，将正方体按图中所示方式展开，则在展开图中B 点的位置为（ ）
A．B．C．D．
11．如图所示的正方体的展开图是（ ）
A． B．
C． D．
12．如图是某个几何体的表面展开图，若围成几何体后，与点E重合的两个点是（ ）
A．C点与D点 B．A点与G点 C．A点与D点 D．A点与C点
二．填空题
13．图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①、②、③、④某一位置，所组成的图形不能围成正方体的位置是___．
14．小强用5个大小一样的正方形制成如图所示的拼接图形（阴影部分），若在图中只添加一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子，这样的拼接方式有_____种．
15．如图所示的三个图中，不是三棱柱的展开图的是_____．（只填序号）
16．要把一个正方体的表面展开成平面图形，至少需要剪开条棱．
17．将一个正方体的表面沿某些棱剪开，展开成一个平面图形（如图），则下列可能的图形有： ．
如图，在边长为20的大正方形中，剪去四个小正方形，可以折成一个无盖的长方体盒子．如果剪去的小正方形边长按整数值依次变化，即分别取1．2．3．…．9．10时，则小正方形边长为 时，所得到的无盖的长方体盒子容积最大．
三．解答题
19．已知：图①、图②、图③均为的正方形网格，在网格中选择2个空白的正方形并涂上阴影，与图中的4个阴影正方形一起构成正方体表面展开图，且3种方法得到的展开图不完全重合．
20．如图是一颗骰子的三种不同的放置方法．
（1）根据图中三种放置方法，推出“？”处的点数．
（2）求这三个骰子下底面上点数和．
21．在把如图折叠成正方体后，
（1）AB与GB的位置关系是 ；
（2）CB与GB的位置关系是 ；
（3）AB与BC的位置关系是 ，理由解释为 ．
22．如图是一个正方体的平面展开图，标注了字母M的是正方体的前面，标注了﹣2的是正方体的底面，正方体的左面与右面标注的式子的和为21．
（1）求x的值；
（2）求正方体的上面和后面的数字的积．
23．在学习《展开与折叠》这一课时，老师让同学们将准备好的正方体或长方体沿某些棱剪开，展开成平面图形．其中，阿中同学不小心多剪了一条棱，把一个长方体纸盒剪成了图①．图②两部分．根据你所学的知识，回答下列问题：
（1）阿中总共剪开了几条棱？
（2）现在阿中想将剪断的图②重新粘贴到图①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，他有几种粘贴方法？请在图①上画出粘贴后的图形（画出一种即可）；
（3）已知图③是阿中剪开的图①的某些数据，求这个长方体纸盒的体积．