北师大版数学 八年级下册 期末 拔高检测卷

这是一份北师大版数学 八年级下册 期末 拔高检测卷，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
满分：120分；时间：100分钟
一、单选题(共10题；共30分)
1．（3分）已知x＞y，则下列不等式不成立的是（ ）
A．﹣3x+6＞﹣3y+6B．2x＞2y
C．﹣3x＜﹣3yD．x﹣6＞y﹣6
2．（3分）等腰三角形两边长分别是2 cm和5 cm，则这个三角形周长是（ ）
A．9 cmB．12 cmC．9 cm或12 cmD．14 cm
3．（3分）如图，观察函数y＝kx+b（k≠0）的图象，关于x的不等式kx+b＜0的解集为（ ）
A．x＞0B．x＜0C．x＜2D．x＞2
4．（3分）若x≠y，则下列分式化简中，正确的是（ ）
A．B．C．D．
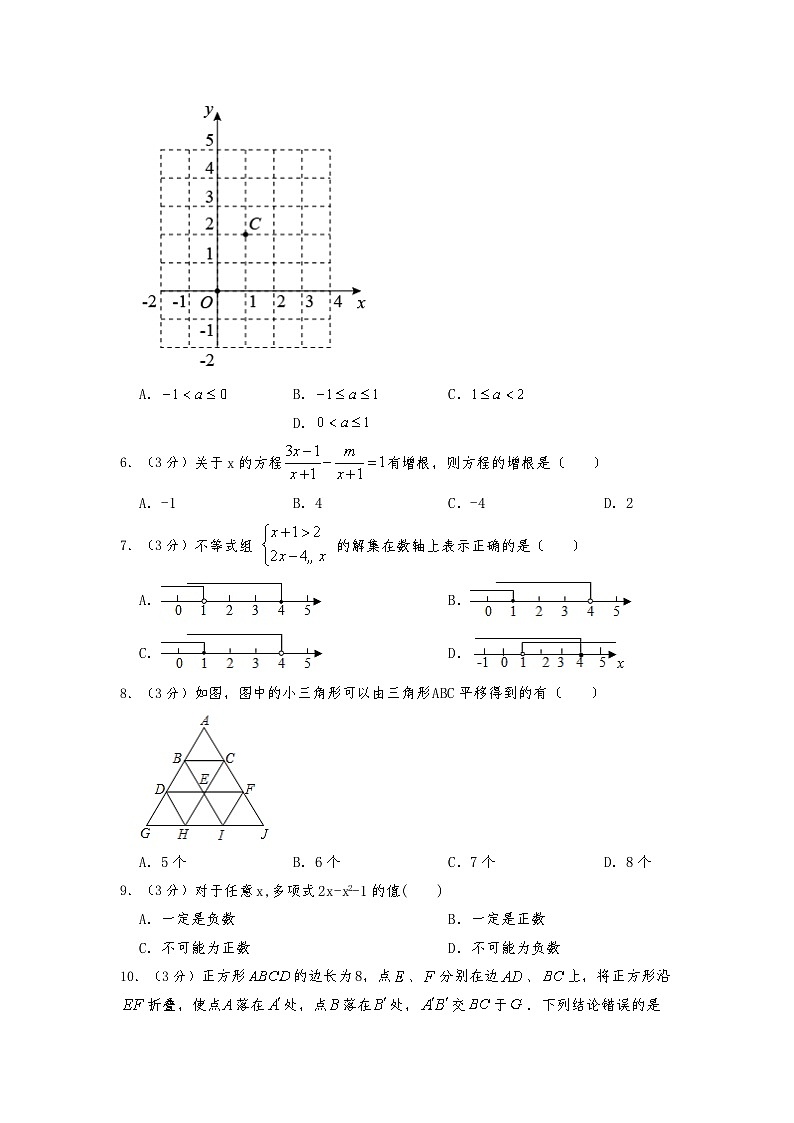
5．（3分）在平面直角坐标系中，点，点，且A在B的下方，点，连接，若在所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为5个，那么a的取值范围是（ ）
A．B．C．D．
6．（3分）关于x的方程有增根，则方程的增根是（ ）
A．-1B．4C．-4D．2
7．（3分）不等式组 的解集在数轴上表示正确的是（ ）
A．B．
C．D．
8．（3分）如图，图中的小三角形可以由三角形ABC平移得到的有（ ）
A．5个B．6个C．7个D．8个
9．（3分）对于任意x,多项式2x-x2-1的值( )
A．一定是负数B．一定是正数
C．不可能为正数D．不可能为负数
10．（3分）正方形的边长为8，点、分别在边、上，将正方形沿折叠，使点落在处，点落在处，交于．下列结论错误的是（ ）
A．当为中点时，则
B．当时，则
C．连接，则
D．当（点不与、重合）在上移动时，周长随着位置变化而变化
二、填空题(共5题；共15分)
11．（3分）因式分解x2y﹣y的正确结果是 ．
12．（3分）已知等腰三角形的一个外角是70°，则它顶角的度数为 ．
13．（3分）如图，一次函数y=-x+1与 的图象相交于点 ，则关于 的不等式 的解集为 .
14．（3分）已知一次函数y=kx+b的图象经过两点A（0，1），B（2，0），则当x 时，y≤0．
15．（3分）数学家莫伦在1925年发现了世界上第一个完美长方形（如图1），即它恰好能被分割成10个大小不同的正方形，从这以后人们开始热衷图形完美分割的研究，□EFGH被分割成13个小正三角形（如图2），已知中间最小的两个正三角形△ABC和△ADC边长均为2，□EFGH的周长为 .
三、解答题(共7题；共75分)
16．（8分）已知：多项式A=b3﹣2ab
（1）（4分）请将A进行因式分解：
（2）（4分）若A=0且a≠0，b≠0，求 的值．
17．（8分）如图，在▱ABCD中，点E、F分别在AD、BC上，且AE=CF．
求证：四边形BFDE是平行四边形．
18．（8分）A、B两地间的距离为15千米，甲从A地出发步行前往B地，20分钟后，乙从 B地出发骑车前往A地，且乙骑车比甲步行每小时多走10千米．乙到达A地后停留40分钟，然后骑车按原路原速返回，结果甲、乙两人同时到达B地．求甲从A地到B地步行所用的时间．
19．（10分）已知正方形ABCD中，点E在边DC上，DE=2，EC=1（如图所示）把线段AE绕点A旋转，使点E落在直线BC上的点F处，求F、C两点的距离.
20．（10分）已知代数式 ，当x=0时，值为2；当x=3时值为1．求x=-3时，代数式的值．
21．（12分）如图，A和B两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A的速度每分钟增加6米，则A和B在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取π=3.14）
22．（19分）如图，CN是等边△ABC的外角∠ACM内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P.
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN＝α，求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA＝x，PC＝y，求PB的长度(用x，y的代数式表示).