人教版（2024）九年级上册24.1.2 垂直于弦的直径多媒体教学ppt课件

这是一份人教版（2024）九年级上册24.1.2 垂直于弦的直径多媒体教学ppt课件，共24页。PPT课件主要包含了学习目标，探一探，总一总，引申定理，辩一辩，推一推，用一用，拓展延伸，垂径定理，自我诊断等内容，欢迎下载使用。
24.1.2垂直于弦的直径 ———（垂径定理）
(1)通过折纸探究圆的对称性，能证明圆是轴对称图形。(2)由圆的轴对称性推导垂径定理及其推论。(3)利用垂径定理解决相应问题。
把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？
结论：圆是轴对称图形。
判断：任意一条直径都是圆的对称轴（ ）
任何一条直径所在的直线都是对称轴。圆有无数条对称轴。
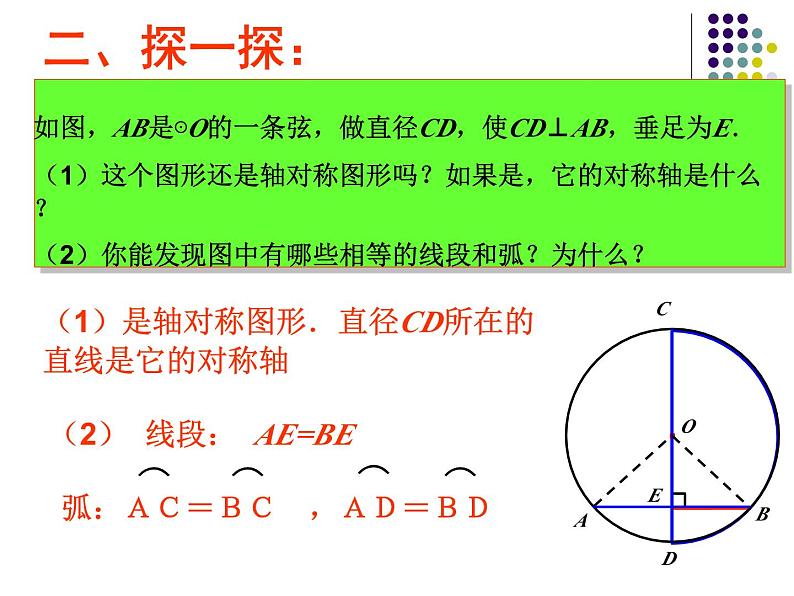
如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．（1）这个图形还是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？
（1）是轴对称图形．直径CD所在的直线是它的对称轴
（2） 线段： AE=BE
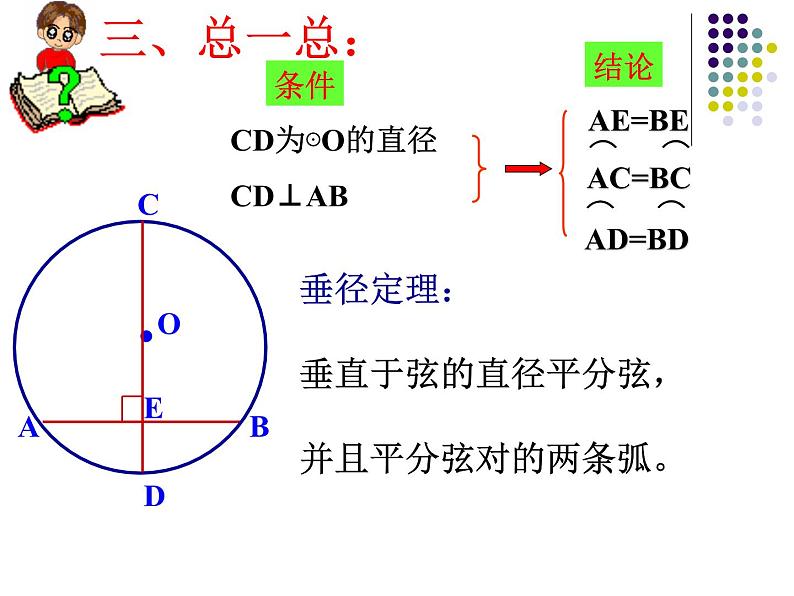
垂径定理：垂直于弦的直径平分弦，并且平分弦对的两条弧。
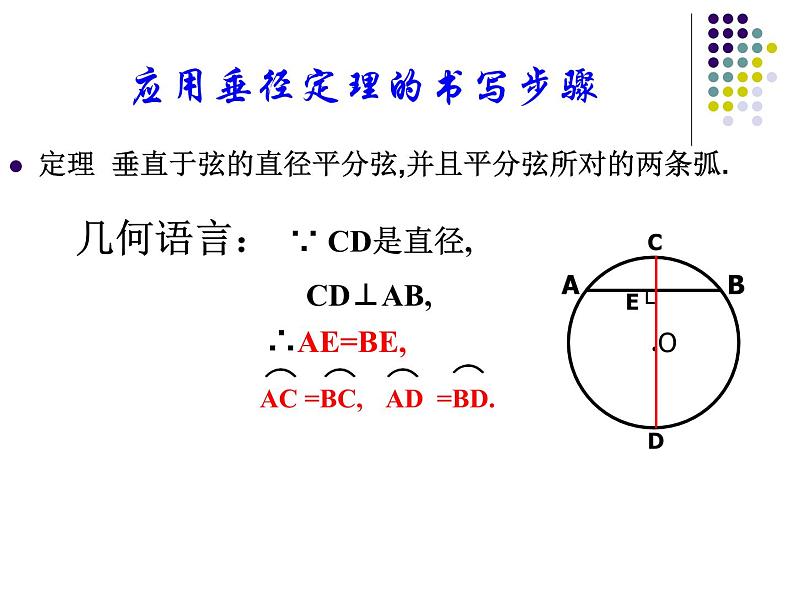
应用垂径定理的书写步骤
定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
几何语言： ∵ CD是直径,
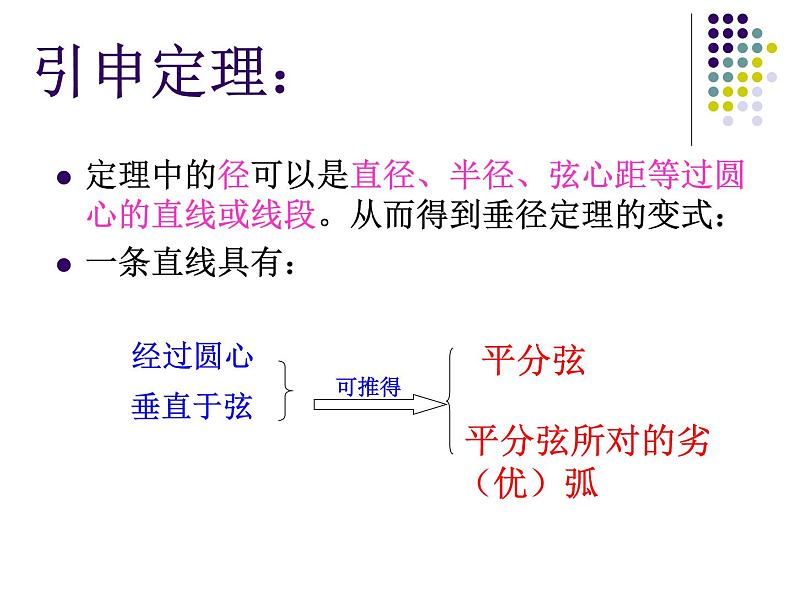
定理中的径可以是直径、半径、弦心距等过圆心的直线或线段。从而得到垂径定理的变式：一条直线具有：
平分弦所对的劣（优）弧
下列图形，符合垂径定理的条件吗？
垂径定理的几个基本图形
垂径定理的推论:平分弦 的直径垂直于弦，并且平分弦所对的两条弧。
“知二推三” (1)垂直于弦 (2)过圆心 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧注意:当具备了(1)(3)时,应对另一 条弦增加”不是直径”的限制.
如图：圆O中，AB是圆O中的一条弦，其中OC⊥AB，圆心到弦的距离用d表示，半径用r表示，弦长用a表示，则d，r，a之间满足什么样的关系呢？
解决有关弦的问题时，经常连接半径；过圆心作一条与弦垂直的线段等辅助线，为应用垂径定理创造条件。 垂径定理经常和勾股定理结合使用。
解：如图，设半径为R，
在Ｒt⊿AOD中，由勾股定理，得
解得 R≈27.9（m）.
答：赵州桥的主桥拱半径约为27.9m.
赵州桥主桥拱的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵州桥主桥拱的半径吗？
六、解决问题：（再逛赵州石拱桥）
1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．
答：⊙O的半径为5cm.
2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
∴四边形ADOE为矩形，
∴ 四边形ADOE为正方形.
∵ OE⊥AC OD⊥AB
已知：如图１，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。求证：AC＝BD。
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.方法规律：利用垂径定理解决问题，通常是根据题意作出辅助线，构造出直角三角形后利用勾股定理解答.
1、教材89页习题24.1　　　 第8题；2、优化设计：轻松尝试应用。
1.过⊙O内一点M的最长的弦长为10㎝,最短弦长为8㎝,那么⊙O的半径是 。
2.已知⊙O的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那么C到AB的距离等于 。
1．半径为4cm的⊙O中，弦AB=4cm, 那么圆心O到弦AB的距离是 。2．⊙O的直径为10cm，圆心O到弦AB的 距离为3cm，则弦AB的长是 。3．半径为2cm的圆中，过半径中点且 垂直于这条半径的弦长是 。
1.如图,在⊙O中,弦AB的长为8cm,圆心到AB的距离为3cm,则⊙O的半径为 .
2.弓形的弦长AB为24cm，弓形的高CD为8cm，则这弓形所在圆的半径为　　　　.