江苏省中考数学模拟题精选按题型分层分类汇编-03填空题（容易题）（含解析）

这是一份江苏省中考数学模拟题精选按题型分层分类汇编-03填空题（容易题）（含解析），共13页。试卷主要包含了实数2的平方根是　 　，＝　 　等内容，欢迎下载使用。
1．（2022•鼓楼区校级二模）写出一个有理数，使这个数的绝对值等于它的倒数： ．
二．科学记数法—表示较大的数（共2小题）
2．（2022•丰县二模）太阳距离银河系中心约为250000000000000000公里，其中数据250000000000000000用科学记数法表示为 ．
3．（2022•海陵区二模）据国家统计局公布，我国第七次全国人口普查结果约为1412000000人，用科学记数法表示为 ．
三．科学记数法—表示较小的数（共3小题）
4．（2022•姜堰区二模）为更好地预防新冠病毒，学校进一步加大了学生核酸检测的比例．核酸中核小体由1lnm×5.5nm的组蛋白核心和盘绕在核心上的DNA构成．其中11nm＝0.000000011m用科学记数法可表示为 m．
5．（2022•武进区二模）新冠疫情期间，佩戴N95口罩是目前核心预防方法之一，N95口罩能够过滤掉的最小的颗粒直径是0.0000003米，其中0.0000003米用科学记数法表示是 米．
6．（2022•镇江二模）随着科技不断发展，芯片的集成度越来越高，我国企业中芯国际已经实现14纳米量产，14纳米＝0.000014毫米，0.000014用科学记数法表示为 ．
四．平方根（共1小题）
7．（2022•姜堰区二模）实数2的平方根是 ．
五．算术平方根（共1小题）
8．（2022•宜兴市二模）＝ ．
六．实数大小比较（共1小题）
9．（2021•石景山区二模）写出一个比0大且比2小的无理数 ．
七．代数式求值（共1小题）
10．（2022•仪征市二模）下列四个代数式①4mn，②m2+4n2，③4m2+n2，④m2+n2，若m＞n＞0，则代数式的值最大的是 ．（填序号）
八．分式有意义的条件（共2小题）
11．（2022•金坛区二模）若代数式有意义，则实数x的取值范围是 ．
12．（2022•泰州二模）若代数式有意义，则实数x的取值范围是 ．
九．二次根式的混合运算（共1小题）
13．（2022•玄武区二模）计算（+1）（﹣）的结果是 ．
一十．一元二次方程的解（共1小题）
14．（2022•武进区二模）若关于x的一元二次方程x2﹣3x﹣k＝0有一个根为1，则k的值为 ．
一十一．点的坐标（共1小题）
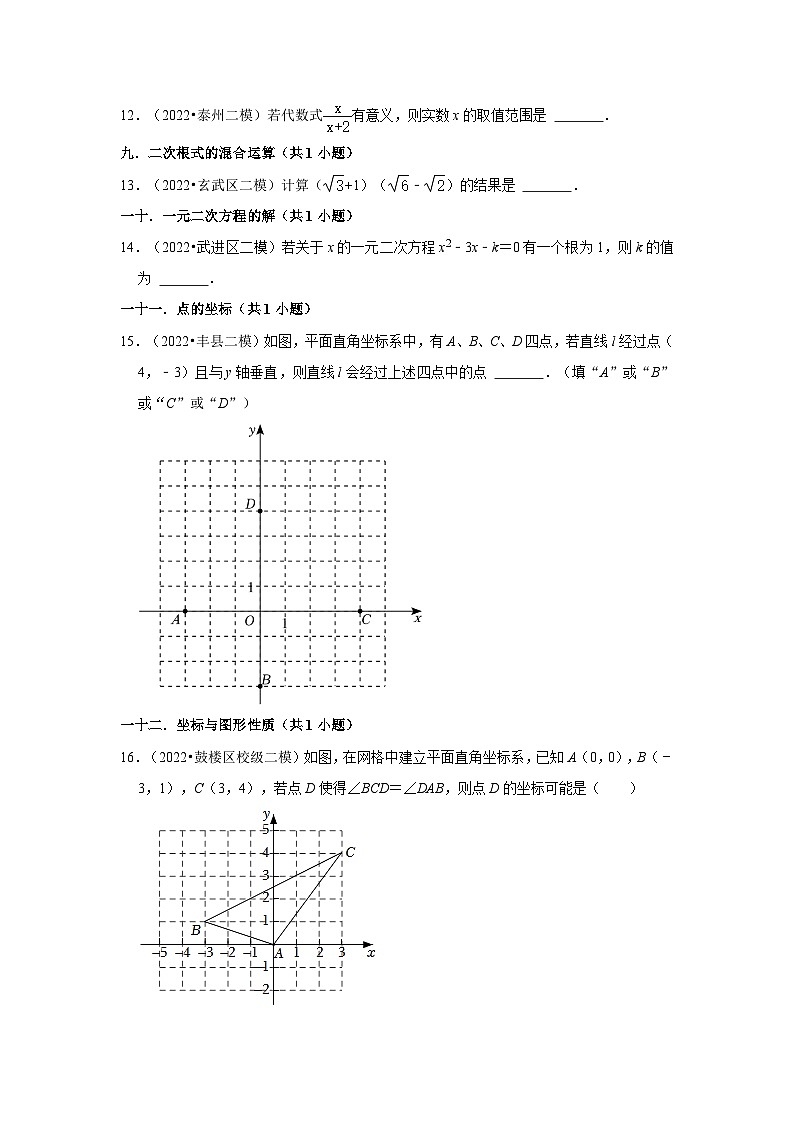
15．（2022•丰县二模）如图，平面直角坐标系中，有A、B、C、D四点，若直线l经过点（4，﹣3）且与y轴垂直，则直线l会经过上述四点中的点 ．（填“A”或“B”或“C”或“D”）
一十二．坐标与图形性质（共1小题）
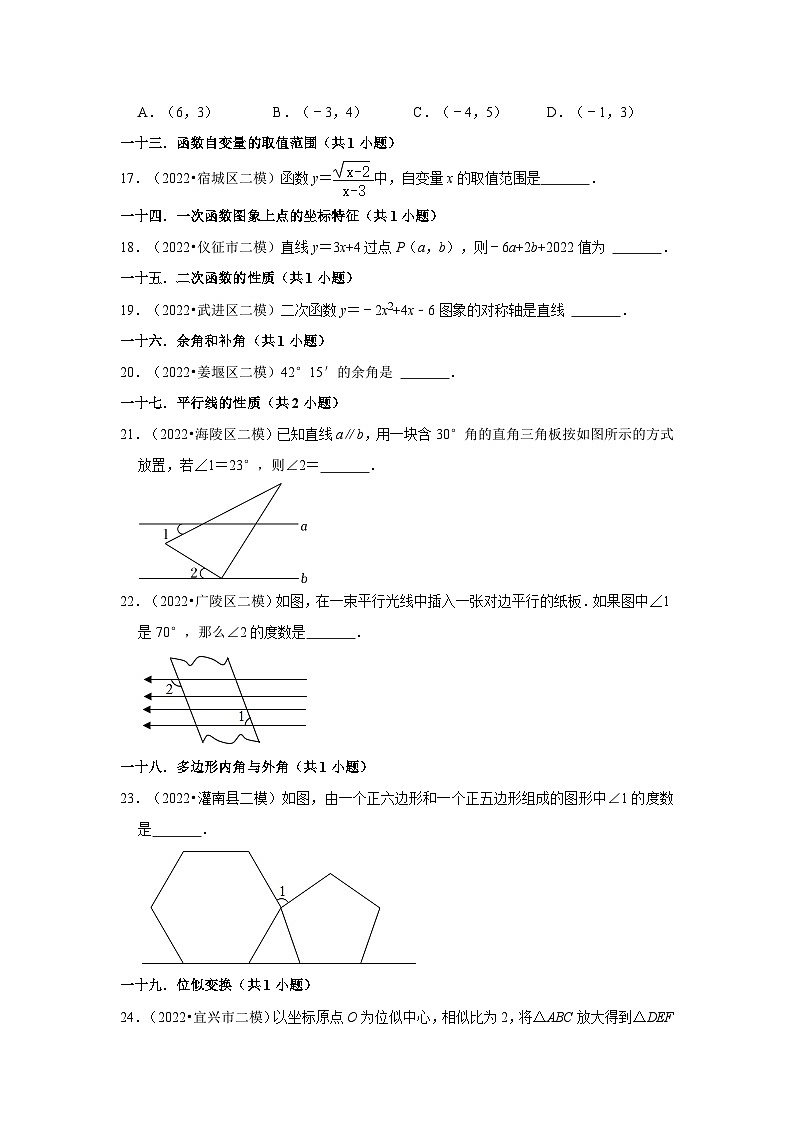
16．（2022•鼓楼区校级二模）如图，在网格中建立平面直角坐标系，已知A（0，0），B（﹣3，1），C（3，4），若点D使得∠BCD＝∠DAB，则点D的坐标可能是（ ）
A．（6，3）B．（﹣3，4）C．（﹣4，5）D．（﹣1，3）
一十三．函数自变量的取值范围（共1小题）
17．（2022•宿城区二模）函数y＝中，自变量x的取值范围是 ．
一十四．一次函数图象上点的坐标特征（共1小题）
18．（2022•仪征市二模）直线y＝3x+4过点P（a，b），则﹣6a+2b+2022值为 ．
一十五．二次函数的性质（共1小题）
19．（2022•武进区二模）二次函数y＝﹣2x2+4x﹣6图象的对称轴是直线 ．
一十六．余角和补角（共1小题）
20．（2022•姜堰区二模）42°15′的余角是 ．
一十七．平行线的性质（共2小题）
21．（2022•海陵区二模）已知直线a∥b，用一块含30°角的直角三角板按如图所示的方式放置，若∠1＝23°，则∠2＝ ．
22．（2022•广陵区二模）如图，在一束平行光线中插入一张对边平行的纸板．如果图中∠1是70°，那么∠2的度数是 ．
一十八．多边形内角与外角（共1小题）
23．（2022•灌南县二模）如图，由一个正六边形和一个正五边形组成的图形中∠1的度数是 ．
一十九．位似变换（共1小题）
24．（2022•宜兴市二模）以坐标原点O为位似中心，相似比为2，将△ABC放大得到△DEF，点C（2，3）的对应点F在第一象限，则点F的坐标为 ．
二十．方差（共1小题）
25．（2022•广陵区二模）四名选手参加射击预选赛，他们成绩的平均环数及方差S2如表所示．如果选出一个成绩较好且状态稳定的人去参赛，则应选 ．
2022年江苏省中考数学模拟题（二模）精选按题型分层分类汇编-03填空题（容易题）
参考答案与试题解析
一．有理数（共1小题）
1．（2022•鼓楼区校级二模）写出一个有理数，使这个数的绝对值等于它的倒数： 1 ．
【解答】解：∵一个数的绝对值等于它的倒数，
∴这个数是1．
故答案为：1．
二．科学记数法—表示较大的数（共2小题）
2．（2022•丰县二模）太阳距离银河系中心约为250000000000000000公里，其中数据250000000000000000用科学记数法表示为 2.5×1017 ．
【解答】解：数据250000000000000000用科学记数法表示为2.5×1017．
故答案为：2.5×1017．
3．（2022•海陵区二模）据国家统计局公布，我国第七次全国人口普查结果约为1412000000人，用科学记数法表示为 1.412×109 ．
【解答】解：1412000000＝1.412×109，
故答案为：1.412×109．
三．科学记数法—表示较小的数（共3小题）
4．（2022•姜堰区二模）为更好地预防新冠病毒，学校进一步加大了学生核酸检测的比例．核酸中核小体由1lnm×5.5nm的组蛋白核心和盘绕在核心上的DNA构成．其中11nm＝0.000000011m用科学记数法可表示为 1.1×10﹣8 m．
【解答】解：0.000000011＝1.1×10﹣8．
故答案为：1.1×10﹣8．
5．（2022•武进区二模）新冠疫情期间，佩戴N95口罩是目前核心预防方法之一，N95口罩能够过滤掉的最小的颗粒直径是0.0000003米，其中0.0000003米用科学记数法表示是 3×10﹣7 米．
【解答】解：0.0000003＝3×10﹣7，
故答案为：3×10﹣7．
6．（2022•镇江二模）随着科技不断发展，芯片的集成度越来越高，我国企业中芯国际已经实现14纳米量产，14纳米＝0.000014毫米，0.000014用科学记数法表示为 1.4×10﹣5 ．
【解答】解：0.000014＝1.4×10﹣5．
故答案为：1.4×10﹣5．
四．平方根（共1小题）
7．（2022•姜堰区二模）实数2的平方根是 ± ．
【解答】解：∵（±）2＝2，
∴2的平方根是±．
故答案为：±．
五．算术平方根（共1小题）
8．（2022•宜兴市二模）＝ 7 ．
【解答】解：＝7，
故答案为：7．
六．实数大小比较（共1小题）
9．（2021•石景山区二模）写出一个比0大且比2小的无理数 （答案不唯一） ．
【解答】解：比0大比2小的无理数都可以，如：，，
故答案为：（答案不唯一）．
七．代数式求值（共1小题）
10．（2022•仪征市二模）下列四个代数式①4mn，②m2+4n2，③4m2+n2，④m2+n2，若m＞n＞0，则代数式的值最大的是 ③ ．（填序号）
【解答】解：∵m＞n＞0，
设m＝2，n＝1，
将m＝2，n＝1代入①，
4nm＝4×2×1＝8；
代入②，
m2+4n2＝22+4×12＝8；
代入③，
4m2+n2＝4×22+12＝17；
代入④，m2+n2＝22+12＝5，
17＞8＞5，
故答案为：③．
八．分式有意义的条件（共2小题）
11．（2022•金坛区二模）若代数式有意义，则实数x的取值范围是 x≠﹣1 ．
【解答】解：由题意得，x+1≠0，
解得x≠﹣1．
故答案是：x≠﹣1．
12．（2022•泰州二模）若代数式有意义，则实数x的取值范围是 x≠﹣2 ．
【解答】解：根据题意得x+2≠0，
解得x≠﹣2，
故答案为：x≠﹣2．
九．二次根式的混合运算（共1小题）
13．（2022•玄武区二模）计算（+1）（﹣）的结果是 2 ．
【解答】解：原式＝×﹣×+1×﹣1×
＝3﹣+﹣
＝2．
故答案为：2．
一十．一元二次方程的解（共1小题）
14．（2022•武进区二模）若关于x的一元二次方程x2﹣3x﹣k＝0有一个根为1，则k的值为 ﹣2 ．
【解答】解：把x＝1代入方程x2﹣3x﹣k＝0，得1﹣3﹣k＝0，
解得k＝﹣2．
故答案为：﹣2．
一十一．点的坐标（共1小题）
15．（2022•丰县二模）如图，平面直角坐标系中，有A、B、C、D四点，若直线l经过点（4，﹣3）且与y轴垂直，则直线l会经过上述四点中的点 B ．（填“A”或“B”或“C”或“D”）
【解答】解：∵直线l经过点（4，﹣3）且与y轴垂直，
∴经过直线l的点纵坐标与点（4，﹣3）纵坐标相等，
∵点B的坐标（0，﹣3），
∴点B符合题意．
故答案为：B．
一十二．坐标与图形性质（共1小题）
16．（2022•鼓楼区校级二模）如图，在网格中建立平面直角坐标系，已知A（0，0），B（﹣3，1），C（3，4），若点D使得∠BCD＝∠DAB，则点D的坐标可能是（ ）
A．（6，3）B．（﹣3，4）C．（﹣4，5）D．（﹣1，3）
【解答】解：当四边形ABCD为平行四边形，
有∠BCD＝∠DAB，
∴AB∥DC，
根据平移原理．所以D（6，3），
故选：A．
一十三．函数自变量的取值范围（共1小题）
17．（2022•宿城区二模）函数y＝中，自变量x的取值范围是 x≥2且x≠3 ．
【解答】解：根据题意得：，
解得：x≥2且x≠3．
故答案是：x≥2且x≠3．
一十四．一次函数图象上点的坐标特征（共1小题）
18．（2022•仪征市二模）直线y＝3x+4过点P（a，b），则﹣6a+2b+2022值为 2030 ．
【解答】解：∵直线y＝3x+4过点P（a，b），
∴b＝3a+4，
∴﹣3a+b＝4，
∴﹣6a+2b+2022＝2（﹣3a+b）+2022＝2×4+2022＝2030．
故答案为：2030．
一十五．二次函数的性质（共1小题）
19．（2022•武进区二模）二次函数y＝﹣2x2+4x﹣6图象的对称轴是直线 x＝1 ．
【解答】解：∵二次函数为：y＝﹣2x2+4x﹣6，
∴对称轴为：x＝﹣＝﹣＝1，
故答案为：x＝1．
一十六．余角和补角（共1小题）
20．（2022•姜堰区二模）42°15′的余角是 47°45′ ．
【解答】解：根据定义，42°15′的余角度数为90°﹣42°15′＝47°45′．
故答案为：47°45′．
一十七．平行线的性质（共2小题）
21．（2022•海陵区二模）已知直线a∥b，用一块含30°角的直角三角板按如图所示的方式放置，若∠1＝23°，则∠2＝ 37° ．
【解答】解：如图，过点P作直线c∥a，则∠3＝∠1＝23°，
∴∠4＝60°﹣23°＝37°，
∵a∥b，
∴c∥b，
∴∠4＝∠2＝37°．
故答案为：37°．
22．（2022•广陵区二模）如图，在一束平行光线中插入一张对边平行的纸板．如果图中∠1是70°，那么∠2的度数是 110° ．
【解答】解：如图所示，由题意可知l∥l'，
∵l∥l'，
∴∠1+∠3＝180°（两直线平行，同旁内角互补），
又∵∠1＝70°，
∴∠3＝110°，
∴∠2＝∠3＝110°（两直线平行，内错角相等）．
故答案为：110°．
一十八．多边形内角与外角（共1小题）
23．（2022•灌南县二模）如图，由一个正六边形和一个正五边形组成的图形中∠1的度数是 84° ．
【解答】解：如图，
由题意得：∠3＝360°÷6＝60°，∠4＝360°÷5＝72°，
则∠2＝180°﹣60°﹣72°＝48°，
所以∠1＝360°﹣48°﹣120°﹣108°＝84°
故答案为84°．
一十九．位似变换（共1小题）
24．（2022•宜兴市二模）以坐标原点O为位似中心，相似比为2，将△ABC放大得到△DEF，点C（2，3）的对应点F在第一象限，则点F的坐标为 （4，6） ．
【解答】解：∵△ABC与△DEF位似．△DEF与△ABC的相似比为2：1，
∴△ABC与△DEF位似比为1：2，
∵点C的坐标为（2，3），
∴点F的坐标为（2×2，3×2），即（4，6），
故答案为：（4，6）．
二十．方差（共1小题）
25．（2022•广陵区二模）四名选手参加射击预选赛，他们成绩的平均环数及方差S2如表所示．如果选出一个成绩较好且状态稳定的人去参赛，则应选 乙 ．
【解答】解：由图可知，乙、丙的平均成绩好，
由于S2乙＜S2丙，故丙的方差大，波动大，应选乙．
故答案为：乙．
甲
乙
丙
丁
平均环数
7
8
8
7
S2
1
1
1.2
1.8
甲
乙
丙
丁
平均环数
7
8
8
7
S2
1
1
1.2
1.8