人教版数学七下重难点培优训练专题8.5 二元一次方程组的应用（三）（2份，原卷版+解析版）

这是一份人教版数学七下重难点培优训练专题8.5 二元一次方程组的应用（三）（2份，原卷版+解析版），文件包含人教版数学七下重难点培优训练专题85二元一次方程组的应用三原卷版doc、人教版数学七下重难点培优训练专题85二元一次方程组的应用三解析版doc等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

【典例1】如图，A、B两地有公路和铁路相连，在这条路上有一家食品厂，它到B地的距离是到A地的2倍，这家厂从A地购买原料，制成食品卖到B地．已知公路运价为1.5元/（公里•吨），铁路运价为1元/（公里•吨），这两次运输（第一次：A地→食品厂，第二次：食品厂→B地）共支出公路运费15600元，铁路运费20600元．
问：（1）这家食品厂到A地的距离是多少？
（2）这家食品厂此次买进的原料每吨5000元，卖出的食品每吨10000元，此批食品销售完后工厂共获利多少元？
【思路点拨】
（1）设这家食品厂到A地的距离是x公里，到B地的距离是y公里，根据食品厂到B地的距离是到A地的2倍且A，B两地间的距离为150公里，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设这家食品厂此次买进的原料m吨，卖出食品n吨，根据两次运输（第一次：A地→食品厂，第二次：食品厂→B地）共支出公路运费15600元、铁路运费20600元，即可得出关于m，n的二元一次方程组，解之即可求出m，n的值，再利用总利润＝销售收入﹣进货成本﹣运费即可求出结论．
【解题过程】
解：（1）设这家食品厂到A地的距离是x公里，到B地的距离是y公里，
根据题意，得：，
解得：．
答：这家食品厂到A地的距离是50公里．
（2）设这家食品厂此次买进的原料m吨，卖出食品n吨，
根据题意得：，
解得：，
∴10000n﹣5000m﹣15600﹣20600＝863800．
答：这家食品厂此批食品销售完共获利863800元．
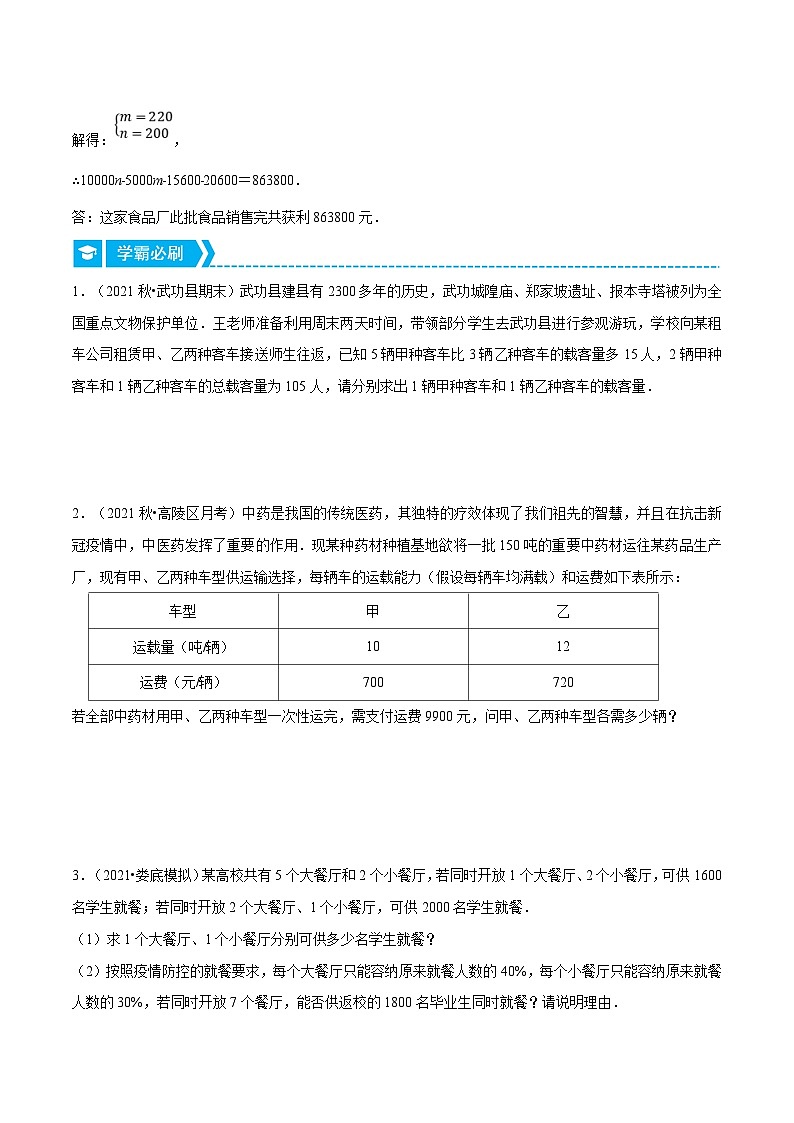
1．（2021秋•武功县期末）武功县建县有2300多年的历史，武功城隍庙、郑家坡遗址、报本寺塔被列为全国重点文物保护单位．王老师准备利用周末两天时间，带领部分学生去武功县进行参观游玩，学校向某租车公司租赁甲、乙两种客车接送师生往返，已知5辆甲种客车比3辆乙种客车的载客量多15人，2辆甲种客车和1辆乙种客车的总载客量为105人，请分别求出1辆甲种客车和1辆乙种客车的载客量．
【思路点拨】
设1辆甲种客车的载客量为x人，1辆乙种客车的载客量为y人，根据“5辆甲种客车比3辆乙种客车的载客量多15人，2辆甲种客车和1辆乙种客车的总载客量为105人”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解答过程】
解：设1辆甲种客车的载客量为x人，1辆乙种客车的载客量为y人，
依题意得：，
解得：．
答：1辆甲种客车的载客量为30人，1辆乙种客车的载客量为45人．
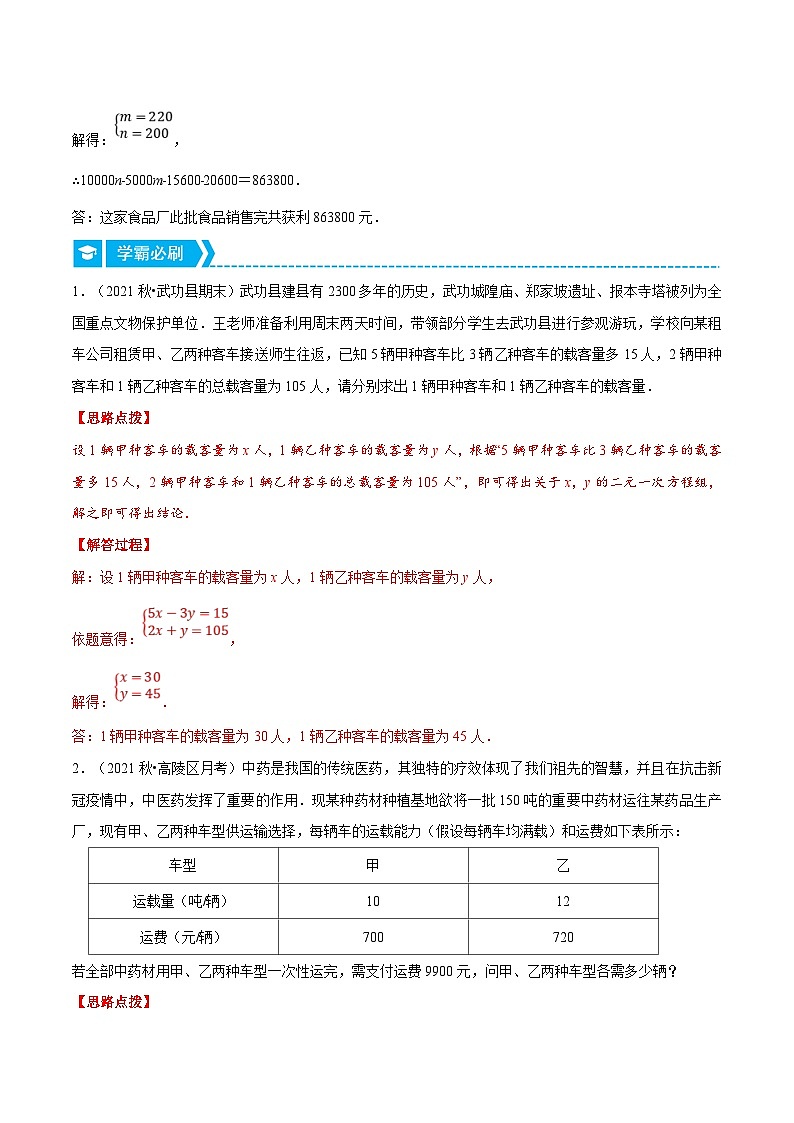
2．（2021秋•高陵区月考）中药是我国的传统医药，其独特的疗效体现了我们祖先的智慧，并且在抗击新冠疫情中，中医药发挥了重要的作用．现某种药材种植基地欲将一批150吨的重要中药材运往某药品生产厂，现有甲、乙两种车型供运输选择，每辆车的运载能力（假设每辆车均满载）和运费如下表所示：
若全部中药材用甲、乙两种车型一次性运完，需支付运费9900元，问甲、乙两种车型各需多少辆？
【思路点拨】
设甲种车型需x辆，乙种车型需y辆，根据运费9900元，总吨数是150，列出方程组，求解即可．
【解答过程】
解：设甲种车型需x辆，乙种车型需y辆，
根据题意得：，
解得：，
答：甲种车型需9辆，乙种车型需5辆．
3．（2021•娄底模拟）某高校共有5个大餐厅和2个小餐厅，若同时开放1个大餐厅、2个小餐厅，可供1600名学生就餐；若同时开放2个大餐厅、1个小餐厅，可供2000名学生就餐．
（1）求1个大餐厅、1个小餐厅分别可供多少名学生就餐？
（2）按照疫情防控的就餐要求，每个大餐厅只能容纳原来就餐人数的40%，每个小餐厅只能容纳原来就餐人数的30%，若同时开放7个餐厅，能否供返校的1800名毕业生同时就餐？请说明理由．
【思路点拨】
（1）设1个大餐厅可供x名学生就餐，1个小餐厅可供y名学生就餐，根据“若同时开放1个大餐厅、2个小餐厅，可供1600名学生就餐；若同时开放2个大餐厅、1个小餐厅，可供2000名学生就餐”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）求出疫情防控期间5个大餐厅和2个小餐厅可供同时就餐的人数，将其与1800比较后即可得出结论．
【解答过程】
解：（1）设1个大餐厅可供x名学生就餐，1个小餐厅可供y名学生就餐，
依题意，得：，
解得：．
答：1个大餐厅可供800名学生就餐，1个小餐厅可供400名学生就餐．
（2）800×5×40%+400×2×30%＝1840（名），
∵1840＞1800，
∴同时开放7个餐厅，能供返校的1800名毕业生同时就餐．
4．（2022•新城区校级二模）为有效落实双减工作，切实做到减负提质，很多学校高度重视学生的体育锻炼，并不定期举行体育比赛．已知在一次足球比赛中，胜一场得3分，平一场得1分，负一场得0分，某队在已赛的11场比赛中保持连续不败，共得25分，求该队获胜的场数．
【思路点拨】
设该队获胜x场，平y场，利用总积分＝3×获胜场次数+1×平的场次数，结合“该队在已赛的11场比赛中保持连续不败，共得25分”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解答过程】
解：设该队获胜x场，平y场，
依题意得：，
解得：．
答：该队获胜7场．
5．（2021春•鼓楼区校级期末）在学校的“科艺节”上，掷飞镖游戏规则如下：如图，掷到A区和B区的得分不同，A区为小圆内部分，B区为大圆内小圆外部分，掷中一次记一次点．现统计小华、小芳和小明掷中与得分情况如下图，那么小明的得分是多少？
【思路点拨】
设掷中A区得x分，掷中B区得y分，根据小华和小芳的得分情况，可得出关于x，y的二元一次方程组，求出x和y的值，此题得解．
【解答过程】
解：设掷到A区和B区的得分分别为x、y分，依题意得：，
解得：，
4x+4y＝76，
答：小明的得分为76．
6．（2021秋•凉州区校级期末）有一个专项加工茶杯车间，一个工人每小时平均可以加工杯身12个，或者加工杯盖15个，车间共有90人，应怎样分配人力，才能使生产的杯身和杯盖正好配套？
【思路点拨】
根据题意可找出两个等量关系为：加工杯身的人数+加工杯盖的人数＝90，加工的杯身的个数＝加工的杯盖的个数，根据这两个等量关系可列出方程组求解即可．
【解答过程】
解：设加工杯身的人数为x人，加工杯盖的人数为y人，由题意，得：
，
解，得．
答：加工杯身的人数为50人，加工杯盖的人数为40人．
7．（2020春•新野县期末）实验室需要一批无盖的长方体模型，一张大纸板可以做成长方体的侧面30个，或长方体的底面25个，一个无盖的长方体由4个侧面和一个底面构成．现有26张大纸板，则用多少张做侧面，多少张做底面才可以使得刚好配套，没有剩余？
【思路点拨】
设用x张做侧面，y张做底面才可以使得刚好配套，没有剩余，根据一个无盖的长方体由4个侧面和一个底面构成．现有26张大纸板，列出方程组，求出x，y的值即可；
【解答过程】
解：设用x张做侧面，y张做底面才可以使得刚好配套，没有剩余，根据题意得：
，
解得：．
答：用20张做侧面，6张做底面才可以使得刚好配套，没有剩余．
8．（2021•沙坪坝区校级开学）已知某服装公司一共有24名工人，所有工人参与制作上衣和裤子，且每个工人只负责制作一项（上衣或裤子），该公司9月以每米80元价格购买了一批布料，该公司用布料分别制作上衣和裤子的相关费用如下表所示，若每月所制作的服装正好配套（一件上衣配一条裤子），则：
（1）求a＝ 18 ，b＝ 6 ．
（2）突发情况，10月该服装公司购进的布料进价比9月上涨了2.5a%，根据市场情况，该公司为了保证运行稳定，只对上衣和裤子的售价进行调整，其他保持不变．10月的上衣售价比9月的售价增加了50元，裤子的售价比9月的售价增加了100元．10月该公司一共能获得的利润是262.8万元，求a的值．（利润＝成品总售价﹣制作总成本﹣布料总成本）
（3）已知该服装公司每月按利润的提成比例来计算每月需发给工人的奖金数，计算方法如下表：
若该公司给工人发放的9月奖金总额为11.28万元，11月和12月该公司获得的总利润为500万元，11月和12月给员工的奖金总额共为49万元，且12月的利润比11月的利润大，求12月该服装公司的利润．
【思路点拨】
（1）根据工人人数为24人，且每月制作的服装配套，列出方程组求解即可；
（2）根据“利润＝成品总售价﹣制作总成本布料总成本”列方程解答即可；
（3）由9月份的利润列方程求出m的值，再根据“11月和12月给员工的奖金总额共为49万元，列方程求解即可．
【解答过程】
解：（1）由题意得，
解得：，
故答案为：18，6；
（2）根据题意得，10月上衣售价950元，裤子售价400元，布料进价80（1+2.5%a），
总售价：（18×300÷1.5）×（950+400）＝3600×（950+400），
制作总成本：180×300×200+6×600×100，
布料总成本：80（1+2.5a%）（18×300+6×600），
3600×（950+400）﹣（18×300×200+6×600×100）﹣80（1+2.5a%）（18×300+6×600）＝2628000，
解得，a＝4，
答：a的值为4；
（3）9月份利润为：
3600×（900+300）﹣（18×300×200+6×600×100）﹣80（18×300+6×600）＝216（万元），
∴200×5%+（216﹣200）×m%＝11.28，
解得，m＝8，
①设12月的利润为x万元，
200×5%+50×8%+20%（x﹣250）+200×5%+（500﹣x﹣200）×8%＝49，
解得x＝425，（500﹣x＜200，不合题意，舍去），
②200×5%+50×8%+20%（x﹣250）+5%（500﹣x）＝49，
解得，x＝400，
答：12月的利润为400万元．
9．（2021春•饶平县校级期末）某饮料加工厂生产的A、B两种饮料均需加入同种派加剂，A饮料每瓶需加该添加剂2克，B饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A、B两种饮料共100瓶，问A、B两种饮料各生产多少瓶？
【思路点拨】
本题需先根据题意设出未知数，再根据题目中的等量关系列出方程组，求出结果即可．
【解答过程】
解：设A饮料生产了x瓶，B饮料生产了y瓶，由题意，得

解得：
答：A饮料生产了30瓶，B饮料生产了70瓶．
10．（2021秋•驻马店期末）医院用甲、乙两种原料为手术后的病人配制营养品，每克甲种原料含0.5单位的蛋白质和1单位铁质，每克乙种原料含0.7单位的蛋白质和0.4单位铁质．若病人每餐需要35单位的蛋白质和40单位铁质，那么每餐甲、乙两种原料各多少克恰能满足病人的需要？
【思路点拨】
本题中可将等量关系列为每餐中甲含的蛋白质的量+乙含的蛋白质的量＝35，每餐中甲含的铁质的量+乙含的铁质的量＝40．由此列出方程组求解．
【解答过程】
解：设每餐需甲原料x克，乙原料y克，
根据题意可列方程组

解得：．
答：每餐需甲种原料28克，乙种原料30克．
11．（2021秋•肃州区期末）5年前母亲的年龄是女儿年龄的15倍，15年后，母亲的年龄比女儿年龄的2倍多6岁．那么现在这对母女的年龄分别是多少？
【思路点拨】
设母亲现在的年龄是x岁，女儿现在的年龄是y岁，根据“5年前母亲的年龄是女儿年龄的15倍，15年后，母亲的年龄比女儿年龄的2倍多6岁”，即可得出关于x，y的二元一次方程组，解之即可得出现在这对母女的年龄．
【解答过程】
解：设母亲现在的年龄是x岁，女儿现在的年龄是y岁，
依题意得：，
解得：．
答：母亲现在的年龄是35岁，女儿现在的年龄是7岁．
12．甲乙两人谈论他们的年龄
甲说：当我是你现在的年龄时，你才十岁；
乙说：当我是你现在的年龄时，你才25岁．
求两人现在的年龄．
【思路点拨】
设甲现在x岁，乙现在y岁，根据题意可得：乙的年龄减去甲乙的年龄差＝10岁，甲的年龄加上甲乙的年龄差＝25岁，据此列方程组求解．
【解答过程】
解：设甲现在x岁，乙现在y岁，
由题意得，，
解得：．
答：甲现在20岁，乙现在15岁．
13．一对母女的年龄之和是80岁，当母亲的年龄是女儿现在年龄的2倍时，女儿的年龄是母亲现在年龄的，女儿和母亲现在的年龄分别是多少？
【思路点拨】
设女儿现在的年龄是x岁，母亲现在的年龄是y岁，根据“母女的年龄之和是80岁，当母亲的年龄是女儿现在年龄的2倍时，女儿的年龄是母亲现在年龄的”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解答过程】
解：设女儿现在的年龄是x岁，母亲现在的年龄是y岁，
依题意得：，
解得：．
答：女儿现在的年龄是25岁，母亲现在的年龄是55岁．
14．甲、乙、丙三人的年龄之和为20岁，甲年龄的2倍比乙大1岁，乙年龄的等于丙的．问甲、乙、丙三人各几岁？
【思路点拨】
设乙的年龄为x岁，丙的年龄为y岁，则甲的年龄为（20﹣x﹣y）岁，根据“甲年龄的2倍比乙大1岁，乙年龄的等于丙的”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解答过程】
解：设乙的年龄为x岁，丙的年龄为y岁，则甲的年龄为（20﹣x﹣y）岁，
依题意，得：，
解得：，
∴20﹣x﹣y＝5．
答：甲的年龄是5岁，乙的年龄是9岁，丙的年龄是6岁．
15．（2022•碑林区校级一模）一个长方形的周长为36厘米，若长减少4厘米，宽增加2厘米，长方形就变成正方形，求正方形的边长．
【思路点拨】
设长方形的长为x厘米，宽为y厘米，由长方形的周长和正方形的边长相等列出二元一次方程组，解方程组，即可解决问题．
【解答过程】
解：设长方形的长为x厘米，宽为y厘米，
由题意得：，
解得：，
则x﹣4＝12﹣4＝8，
答：正方形的边长为8厘米．
16．（2021秋•浑南区期末）如图，用10块相同的小长方形地砖拼成一个宽是75厘米的大长方形，用列方程或方程组的方法，求每块小长方形地砖的长和宽分别是多少厘米？
【思路点拨】
设小长方形地砖的长为x厘米，宽为y厘米，由大长方形的宽为75厘米，即可得出关于x、y的二元一次方程组，解之即可得出结论．
【解答过程】
解：设小长方形地砖的长为x厘米，宽为y厘米，
根据题意得：，
解得：．
答：小长方形地砖的长为45厘米，宽为15厘米．
17．（2021春•运城月考）若用长为acm，宽为bcm的相同的8块小长方形拼成一个大正方形（如图），且图中阴影部分为边长为3cm的小正方形．每个小长方形的面积是多少？
【思路点拨】
观察图形，根据小长方形长与宽之间的关系，即可得出关于a，b的二元一次方程组，解之即可得出a，b的值，再利用长方形的面积计算公式，即可求出每个小长方形的面积．
【解答过程】
解：依题意得：，
解得：，
∴ab＝5×4＝20．
答：每个小长方形的面积是20cm2．
18．（2021春•舞阳县期末）如图，在长方形ABCD中，放入六个形状大小相同的长方形，所标尺寸如图所示，请你利用方程组的思想方法求出图中阴影部分面积是多少cm2？
【思路点拨】
设小长方形的长为xcm，宽为ycm，观察图形即可列出关于x、y的二元一次方程组，解之即可得出x、y的值，再根据阴影部分的面积＝大长方形的面积﹣6个小长方形的面积，即可求出结论．
【解答过程】
解：设小长方形的长为xcm，宽为ycm，
根据题意得：，
解得：，
∴S阴影＝14×（6+2×2）﹣8×2×6＝44（cm2）．
答：图中阴影部分面积是44cm2．
19．（2021春•饶平县校级期末）某种物品包装盒的侧面展开图如图，如果长方体盒子的长比宽多40cm，求这个长方体的体积．
【思路点拨】
首先设长方体盒子的宽为x（cm），则长为（x+40）cm，高为y（cm）．根据等量关系：长+高×2＝130，宽×2+高×2＝140列方程组，进一步求出长、宽、高，再进一步求得体积即可．
【解答过程】
解：设此盒的宽为x（cm），则长为（x+40）cm，高为y（cm）．
根据题意，得
解得
体积为x（x+40）y＝50×（50+40）×20＝90000（cm3）．
20．（2021春•江岸区月考）某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）
（1）若该厂购进正方形纸板1000张，长方形纸板2000张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；
（2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜n＜136，且一个竖式纸箱成本300元，一个横式纸箱成本200元，试求在这一天加工两种纸箱时，a的所有可能值中，成本最低花费多少元？
【思路点拨】
（1）设加工竖式纸盒x个，加工横式纸盒y个，根据两种纸盒每个各需长方形和正方形纸板的张数结合共用正方形纸板1000张、长方形纸板2000张，列出二元一次方程组，解之即可得出结论；
（2）设加工竖式纸盒m个，加工横式纸盒n个，根据两种纸盒每个各需长方形和正方形纸板的张数结合共用正方形纸板50张、长方形纸板a张，列出m、n的二元一次方程组，解之即可用含a的代数式表示出n值，再根据n、a为正整数结合120＜a＜136即可求出a的值，即可解决问题．
【解答过程】
解：（1）设加工竖式纸盒x个，加工横式纸盒y个，
根据题意得：，
解得：，
答：加工竖式纸盒200个，加工横式纸盒400个，恰好能将购进的纸板全部用完；
（2）设加工竖式纸盒m个，加工横式纸盒n个，
根据题意得：，
∴n＝40，
∵n、a为正整数，
∴a为5的倍数，
又∵120＜a＜136，
∴满足条件的a为：125，130，135，
当a＝125时，n＝15，m＝20，成本费为：300×20+200×15＝9000（元）；
当a＝130时，n＝14，m＝22，成本费为：300×22+200×14＝9400（元）；
当a＝135时，n＝13，m＝24，成本费为：300×24+200×13＝9800（元）；
∵9000＜9400＜9800，
∴a的所有可能值中，成本最低花费9000元．车型
甲
乙
运载量（吨/辆）
10
12
运费（元/辆）
700
720
制作成品
所需工人（人）
每个工人每月所需布料（米）
每件所需布料（米）
成品售价
（元/件）
平均每制作1米消耗的成本（元）
上衣
a
300
1.5
900
200
裤子
b
600
1
300
100
制作的利润
不超过200万元的部分
超过200万元但不超过250万元的部分
超过250万元的部分
提成比例
5%
m%
20%