人教版（2024）七年级下册7.1.2平面直角坐标系精品单元测试综合训练题

这是一份人教版（2024）七年级下册7.1.2平面直角坐标系精品单元测试综合训练题，文件包含人教版数学七下同步培优训练专题77第7章平面直角坐标系单元测试能力过关卷原卷版doc、人教版数学七下同步培优训练专题77第7章平面直角坐标系单元测试能力过关卷解析版doc等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2021秋•成都期末）在平面直角坐标系中，下列各点位于第四象限的是（ ）
A．（2，3）B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）
2．（2021秋•芝罘区期末）在平面直角坐标系中，第四象限内有一点M，它到x轴的距离为3，到y轴的距离为4，则点M的坐标为（ ）
A．（﹣3，4）B．（﹣4，3）C．（3，﹣4）D．（4，﹣3）
3．（2021秋•凤翔县期末）若点P（m，n）在第三象限，则点Q（﹣m，﹣n）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．（2021秋•苏州期末）若点P（a+2，a）在y轴上，则点P的坐标为（ ）
A．（﹣2，0）B．（0，﹣2）C．（2，0）D．（0，2）
5．（2021春•海口期末）在平面直角坐标系中，将点（﹣2，3）向右平移6个单位长度后得到的点的坐标（ ）
A．（4，3）B．（﹣6，3）C．（﹣2，7）D．（﹣2，﹣1）
6．（2020秋•福州期末）将点（3，1）绕原点顺时针旋转90°得到的点的坐标是（ ）
A．（﹣3，﹣1）B．（1，﹣3）C．（3，﹣1）D．（﹣1，3）
7．（2017秋•淮安月考）坐标平面上有P，Q两点，其坐标分别为（b，a）、（﹣b，a），则P、Q两点的位置关系为（ ）
A．关于x轴对称B．关于y轴对称
C．关于原点对称D．将P点向左平移b个单位
8．（2021春•栾城区期中）如图，若在象棋盘上建立平面直角坐标系，使棋子“车”的坐标为（﹣2，2），“马”的坐标为（1，2），则棋子“炮”的坐标为（ ）
A．（3，2）B．（3，1）C．（2，2）D．（﹣2，2）
9．（2021春•越秀区期末）课间操时，小华、小军、小刚的位置如图所示．如果小军的位置用（0，0）表示，小华的位置用（﹣2，﹣1）表示，那么小刚的位置可以表示成（ ）
A．（2，2）B．（2，3）C．（3，4）D．（4，3）
10．（2018秋•明山区校级期中）如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中（1，0）→（2，0）→（2，1）→（1，1）→（1，2）→（2，2）…根据这个规律，则第2018个点的纵坐标为（ ）
A．6B．7C．8D．9
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2018春•镇康县期中）剧院里5排2号可以用（5，2）表示，则（7，9）表示 ．
12．（2018春•吴忠期末）在平面直角坐标系中，点P（4，﹣5）到x轴的距离为 ．
13．（2018秋•高要区期中）点A（﹣5，﹣3）关于x轴对称的点的坐标是 ．
14．（2021春•通州区期末）如图，在象棋棋盘上建立平面直角坐标系，如果使“帅”的位置为点（0，﹣2），“相”的位置为点（2，﹣2），那么“炮”的位置为点 ．
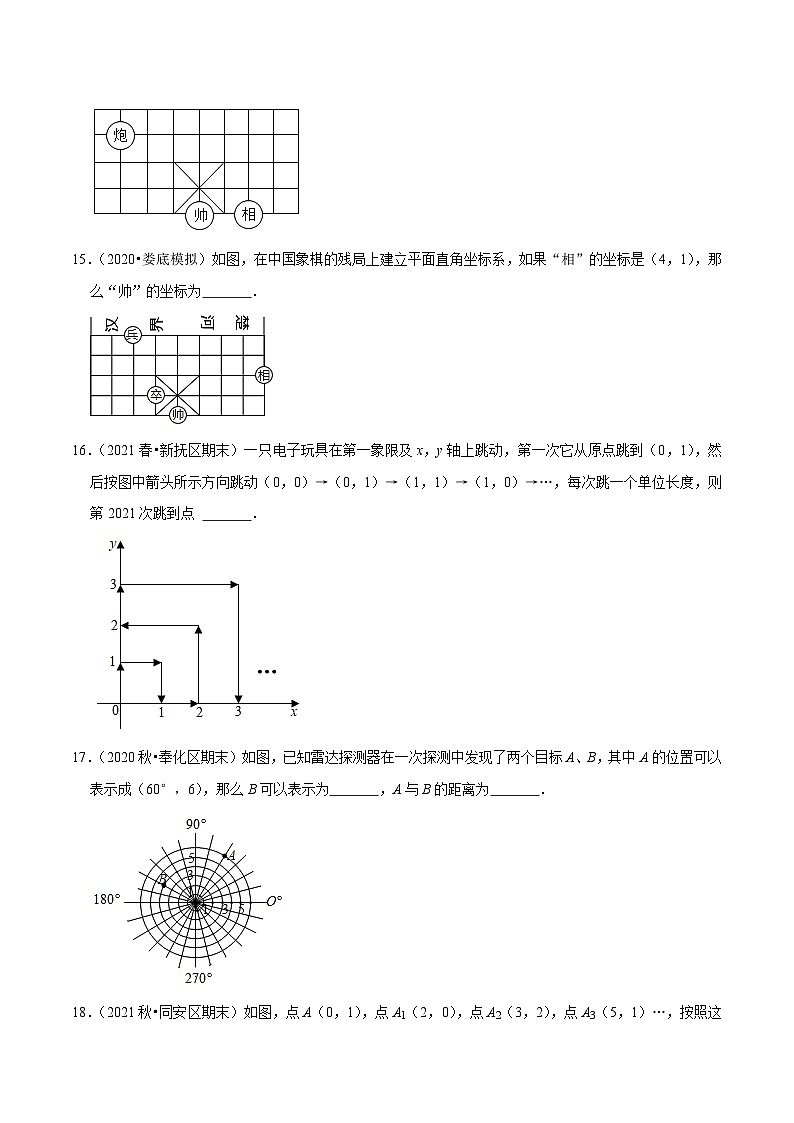
15．（2020•娄底模拟）如图，在中国象棋的残局上建立平面直角坐标系，如果“相”的坐标是（4，1），那么“帅”的坐标为 ．
16．（2021春•新抚区期末）一只电子玩具在第一象限及x，y轴上跳动，第一次它从原点跳到（0，1），然后按图中箭头所示方向跳动（0，0）→（0，1）→（1，1）→（1，0）→…，每次跳一个单位长度，则第2021次跳到点 ．
17．（2020秋•奉化区期末）如图，已知雷达探测器在一次探测中发现了两个目标A、B，其中A的位置可以表示成（60°，6），那么B可以表示为 ，A与B的距离为 ．
18．（2021秋•同安区期末）如图，点A（0，1），点A1（2，0），点A2（3，2），点A3（5，1）…，按照这样的规律下去，点A2021的坐标为 ．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2018秋•德清县期末）在平面直角坐标系xOy中，△ABC的位置如图所示
（1）分别写出△ABC各个顶点的坐标：
A（ ， ）；B（ ， ）
C（ ， ）
（2）顶点A关于x轴对称的点A′的坐标（ ， ），顶点C关于原点对称的点C的坐标（ ， ）
（3）△ABC的面积为 ．
20．（2020春•桃江县期末）如图，△ABC的三个顶点坐标分别为A（0，2），B（﹣3，1），C（﹣2，﹣2）．
（1）将△ABC向右平移2个单位，作出△A'B'C'；
（2）写出△A'B'C'的顶点坐标．
21．（2021秋•凤翔县期中）已知点A（a﹣1，5）和B（2，b﹣1），试根据下列条件求出a，b的值．
（1）A，B两点关于y轴对称；
（2）A，B两点关于x轴对称；
（3）AB∥x轴．
22．（2021秋•长丰县期末）如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行，从内到外，它们的边长依次为2、4、6、8、…，顶点依次用A1、A2、A3、A4、…表示．
（1）请直接写出A5、A6、A7、A8的坐标；
（2）根据规律，求出A2022的坐标．
23．（2021秋•姑苏区期中）如图，方格纸中每个小方格都是边长为1个单位的正方形，学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答下列问题：
（1）在图中建立平面直角坐标系，并标出坐标原点O；
（2）若体育馆位置坐标为C（1，3），请在坐标系中标出体育馆的位置C；
（3）点C绕原点顺时针旋转90°得到点D，直接写出点D的坐标；
（4）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．
24．（2021秋•漳州期末）在平面直角坐标系xOy中，给出如下定义：点A到x轴、y轴距离的较大值称为点A的“长距”，当点P的“长距”等于点Q的“长距”时，称P，Q两点为“等距点”．
（1）求点A（﹣5，2）的“长距”；
（2）若C（﹣1，k+3），D（4，4k﹣3）两点为“等距点”，求k的值．