人教版数学七年级下册期中解答题压轴必刷常考题（2份，原卷版+解析版）

这是一份人教版数学七年级下册期中解答题压轴必刷常考题（2份，原卷版+解析版），文件包含人教版数学七年级下册期中解答题压轴必刷常考题原卷版doc、人教版数学七年级下册期中解答题压轴必刷常考题解析版doc等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
1．（安溪）如图，将一条数轴在原点O和点B处各折一下，AO∥BC，得到一条“折线数轴”．图中点A表示﹣20，点B表示20，点C表示36．动点M从点A出发，以2个单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点N从点C出发，以1个单位/秒的速度沿着“折线数轴”的负方向运动，从点B运动到点O期间的速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．
（1）填空：点A和点C在数轴上相距 56 个单位长度；
（2）当t为何值时，点M与点N相遇？
（3）当t为何值时，M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等．
【答案】（1）56 （2） t＝ （3）t的值为4或13或22或34
【解答】解：（1）∵点A表示﹣20，点C表示36，
∴点A和点C在数轴上相距36﹣（﹣20）＝56（个单位长度），
故答案为：56；
（2）由题意知，N从C到B需16s，M从A到O需10s，
∴M、N在OB段相遇，
根据题意得：20+（t﹣10）+16+2（t﹣16）＝56，
解得t＝，
答：t为时，点M与点N相遇；
（3）分四种情况：
①当点M在AO上，点N在CB上时，OM＝20﹣2t，BN＝16﹣t，
∴20﹣2t＝16﹣t，
解得t＝4，
②当M在OB上，N在CB上时，OM＝t﹣10，BN＝16﹣t，
∴t﹣10＝16﹣t，
解得t＝13，
③当M在OB上，N在OB上时，OM＝t﹣10，BN＝2（t﹣16），
∴t﹣10＝2（t﹣16），
解得t＝22，
④当M在BC上，N在OA上时，
20+2（t﹣30）＝20+（t﹣26），
解得t＝34，
综上所述，t的值为4或13或22或34时，M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等．
2．（朝阳）将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起，其中∠A＝60°，∠D＝30°，∠E＝∠B＝45°．
（1）若∠1＝25°，则∠2的度数为 ；
（2）直接写出∠1与∠3的数量关系： ；
（3）直接写出∠2与∠ACB的数量关系： ；
（4）如图2，当∠ACE＜180°且点E在直线AC的上方时，将三角尺ACD固定不动，改变三角尺BCE的位置，但始终保持两个三角尺的顶点C重合，这两块三角尺是否存在一组边互相平行？请直接写出∠ACE角度所有可能的值 ．
【答案】（1）65°（2） ∠1＝∠3； （3） ∠2+∠ACB＝180°（4）30°或45°或120°或135°或165°．
【解答】解：（1）∵∠1＝25°，∠ACD＝90°，
∴∠2＝∠ACD﹣∠1＝65°，
故答案为：65°；
（2）∵∠1+∠2＝∠ACD＝90°，∠2+∠3＝∠BCE＝90°，
∴∠1+∠2＝∠2+∠3，
∴∠1＝∠3，
故答案为：∠1＝∠3；
（3）∵∠ACD＝∠BCE＝90°，
∴∠ACB+∠2
＝∠1+∠2+∠3+∠2
＝∠ACD+∠BCE
＝180°，
即∠2+∠ACB＝180°，
故答案为：∠2+∠ACB＝180°；
（4）存在，
①当BC∥AD时，
∵BC∥AD，
∴∠BCD＝∠D＝30°，
∴∠ACB＝90°+30°＝120°，
∴∠ACE＝∠ACB﹣∠BCE＝120°﹣90°＝30°；
②当BE∥AC时，如图，
∵BE∥AC，
∴∠ACE＝∠E＝45°；
③当AD∥CE时，如图，
∵AD∥CE，
∴∠DCE＝∠D＝30°，
∴∠ACE＝90°+30°＝120°；
④当BE∥CD时，如图，
∵BE∥CD，
∴∠DCE＝∠E＝45°，
∴∠ACE＝∠ACD+∠DCE＝135°；
⑤当BE∥AD时，如图，
过点C作CF∥AD，
∵BE∥AD，CF∥AD，
∴BE∥AD∥CF，
∴∠ECF＝∠E＝45°，∠DCF＝∠D＝30°，
∴∠DCE＝30°+45°＝75°，
∴∠ACE＝90°+75°＝165°．
综上所述：当∠ACE＝30°或45°或120°或135°或165°时，有一组边互相平行．
故答案为：30°或45°或120°或135°或165°．
3．（淇县）如图（1），AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．
解：猜想∠BPD+∠B+∠D＝360°
理由：过点P作EF∥AB，
∴∠B+∠BPE＝180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D＝180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D＝360°
∴∠B+∠BPD+∠D＝360°
（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．
（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．
【答案】（1） ∠BPD＝∠B+∠D（2）∠BPD＝∠B﹣∠D．
【解答】解：（1）∠BPD＝∠B+∠D．
理由：如图2，过点P作PE∥AB，
∵AB∥CD，
∴PE∥AB∥CD，
∴∠1＝∠B，∠2＝∠D，
∴∠BPD＝∠1+∠2＝∠B+∠D；
（2）如图（3）：∠BPD＝∠D﹣∠B．
理由：∵AB∥CD，
∴∠1＝∠D，
∵∠1＝∠B+∠P，
∴∠D＝∠B+∠P，
即∠BPD＝∠D﹣∠B；
如图（4）：∠BPD＝∠B﹣∠D．
理由：∵AB∥CD，
∴∠1＝∠B，
∵∠1＝∠D+∠P，
∴∠B＝∠D+∠P，
即∠BPD＝∠B﹣∠D．
4．（西乡塘）如图，已知DC∥FP，∠1＝∠2，∠DEF＝30°，∠AGF＝70°，FH平分∠EFG．
（1）求证：DC∥AB；
（2）求∠PFH的度数．
【答案】（1）略 （2）∠PFH的度数为20°
【解答】解：（1）∵DC∥FP，
∴∠C＝∠2，
又∵∠1＝∠2，
∴∠C＝∠1，
∴DC∥AB；
（2）∵DC∥FP，DC∥AB，∠DEF＝30°，
∴∠DEF＝∠EFP＝30°，AB∥FP，
又∵∠AGF＝70°，
∴∠AGF＝∠GFP＝70°，
∴∠GFE＝∠GFP+∠EFP＝70°+30°＝100°，
又∵FH平分∠EFG，
∴∠GFH＝∠GFE＝50°，
∴∠PFH＝∠GFP﹣∠GFH＝70°﹣50°＝20°．
答：∠PFH的度数为20°．
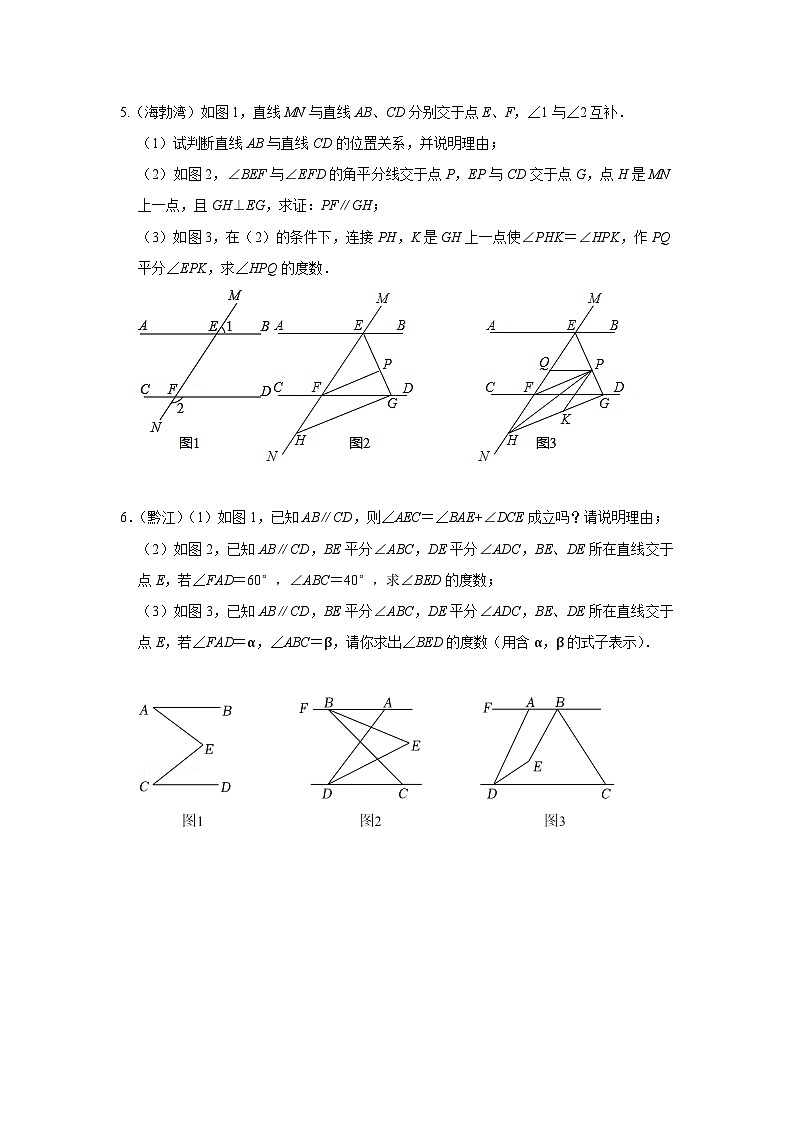
5.（海勃湾）如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．
（1）试判断直线AB与直线CD的位置关系，并说明理由；
（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；
（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PQ平分∠EPK，求∠HPQ的度数．
【答案】（1）AB∥CD （2）PF∥GH（3）∠HPQ的度数为45°
【解答】解：（1）AB∥CD，
理由如下：
∵∠1与∠2互补，
∴∠1+∠2＝180°，
又∵∠1＝∠AEF，∠2＝∠CFE，
∴∠AEF+∠CFE＝180°，
∴AB∥CD；
（2）由（1）知，AB∥CD，
∴∠BEF+∠EFD＝180°．
又∵∠BEF与∠EFD的角平分线交于点P，
∴，
∴∠EPF＝90°，即EG⊥PF．
∵GH⊥EG，
∴PF∥GH；
（3）∵∠PHK＝∠HPK，∴∠PKG＝2∠HPK．
又∵GH⊥EG，
∴∠KPG＝90°﹣∠PKG＝90°﹣2∠HPK．
∴∠EPK＝180°﹣∠KPG＝90°+2∠HPK．
∵PQ平分∠EPK，
∴．
∴∠HPQ＝∠QPK﹣∠HPK＝45°．
答：∠HPQ的度数为45°．
6．（黔江）（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由；
（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠FAD＝60°，∠ABC＝40°，求∠BED的度数；
（3）如图3，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠FAD＝α，∠ABC＝β，请你求出∠BED的度数（用含α，β的式子表示）．
【答案】（1） 成立 （2） ∠BED＝50°（3）
【解答】解：（1）成立，
理由：如图1中，作EF//AB，则有EF//CD，
∴∠1＝∠BAE，∠2＝∠DCE，
∴∠AEC＝∠1+∠2＝∠BAE+∠DCE；
（2）如图2，过点E作EH//AB，
∵AB//CD，∠FAD＝60°，
∴∠FAD＝∠ADC＝60°，
∵DE平分∠ADC，∠ADC＝60°，
∴，
∵BE平分∠ABC，∠ABC＝40°，
∴，
∵AB//CD，
∴AB//CD//EH，
∴∠ABE＝∠BEH＝20°，∠CDE＝∠DEH＝30°，
∴∠BED＝∠BEH+∠DEH＝50°．
（3）如图3，过点E作EG//AB，
∵BE平分∠ABC，DE平分∠ADC，∠ABC＝β，∠ADC＝∠FAD＝α，
∴，，
∵AB//CD，
∴AB//CD//EG，
∴，，
∴．
7．（拱墅）小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下．
（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由．
（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠FAD＝50°，∠ABC＝40°，求∠BED的度数．
【答案】（1）∠AEC＝∠BAE+∠DCE． （2）∠BED＝45°
【解答】解：（1）∠AEC＝∠BAE+∠DCE成立，理由：
过点E作EF∥AB，如图，
∵EF∥AB，
∴∠A＝∠AEF．
∵EF∥AB，AB∥CD，
∴FE∥CD．
∴∠C＝∠CEF．
∵∠AEC＝∠AEF+∠CEF，
∴∠AEC＝∠BAE+∠DCE．
（2）过点E作EH∥AB，如图，
由（1）的结论可得：∠BED＝∠ABE+∠EDC，
∵BE平分∠ABC，∠ABC＝40°，
∴∠ABE＝∠ABC＝20°．
∵∠FAD＝50°，AB∥CD，
∴∠ADC＝∠FAD＝50°．
∵DE平分∠ADC，
∴∠EDC＝∠ADC＝25°．
∴∠BED＝20°+25°＝45°．
8．（宜兴）如图①，已知PQ∥MN，且∠BAM＝2∠BAN．
（1）填空：∠PBA＝ °；
（2）如图（1）所示，射线AM绕点A开始顺时针旋转至AN便立即按原速度回转至AM位置，射线BP绕点B开始顺时针旋转至BQ便立即按原速度回转至BP位置．若AM转动的速度是每秒2度，BP转动的速度是每秒1度，若射线BP先转动30秒，射线AM才开始转动，在射线BP到达BQ之前，射线AM转动几秒，两射线互相平行？
（3）如图（2），若两射线分别绕点A，B顺时针方向同时转动，速度同题（2），在射线AM到达AN之前，若两射线交于点C，过C作∠ACD交PQ于点D，且∠ACD＝120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由．
【答案】（1） 120（2） AM转动30秒或110秒（3）∠BAC＝2∠BCD
【解答】解：（1）∵∠BAM＝2∠BAN，∠BAM+∠BAN＝180°，
∴∠BAM＝120°．
∵PQ∥MN，
∴∠PBA＝∠BAM＝120°．
故答案为：120；
（2）设射线AM转动t秒，两射线互相平行，
当0＜t＜90时，如图，AM′和BP′为经过t秒后AM，BP旋转的位置，
则∠MAM′＝2t°，∠PBP′＝（t+30）°，
∵PQ∥MN，
∴∠BM′A＝∠MAM′＝2t°，
∵AM′∥BP′，
∴∠AM′B＝∠PBP′．
∴2t＝t+30．
解得：t＝30；
当90＜t＜150时，如图，AM′和BP′为经过t秒后AM，BP旋转的位置，
则∠MAM′＝（360﹣2t）°，∠PBP′＝（t+30）°，
∵PQ∥MN，
∴∠BM′A＝∠MAM′＝2t°，
∵AM′∥BP′，
∴∠AM′B＝∠PBP′．
∴360﹣2t＝t+30．
解得：t＝110．
综上所述，当射线AM转动30秒或110秒时，两射线互相平行．
（3）∠BAC与∠BCD的数量关系不会发生变化，∠BAC＝2∠BCD．理由：
设射线AM，BP转动时间为m秒，
∴∠BAC＝（2m﹣120）°，∠ABC＝（120﹣t）°，
∴∠ACB＝180°﹣（2m﹣120）°﹣（120﹣m）°＝（180﹣m）°．
∵∠ACD＝120°，
∴∠BCD＝120°﹣（180﹣m）°＝（m﹣60）°．
∵2m﹣120＝2（m﹣60），
∴∠BAC＝2∠BCD．
∴∠BAC与∠BCD的数量关系不会发生变化，∠BAC＝2∠BCD．
9．（仁寿）如图①．已知AM∥CN，点B为平面内一点，AB⊥BC于点B，过点B作BD⊥AM于点D，设∠BCN＝α．
（1）若α＝30°，求∠ABD的度数；
（2）如图②，若点E、F在DM上，连接BE、BF、CF，使得BE平分∠ABD、BF平分∠DBC，求∠EBF的度数；
（3）如图③，在（2）问的条件下，若CF平分∠BCH，且∠BFC＝3∠BCN，求∠EBC的度数．
【答案】（1）30° （2） 45°（3）97.5°．
【解答】解：（1）延长DB，交NC于点H，如图，
∵AM∥CN，BD⊥AM，
∴DH⊥NC．
∴∠BHC＝90°．
∵∠BCN＝α＝30°，
∴∠HBC＝90°﹣∠BCN＝60°．
∵AB⊥BC，
∴∠ABC＝90°．
∴∠ABD＝180°﹣∠ABC﹣∠HBC＝30°；
（2）延长DB，交NC于点H，如图，
∵AM∥CN，BD⊥AM，
∴DH⊥NC．
∴∠BHC＝90°．
∵∠BCN＝α，
∴∠HBC＝90°﹣α．
∵AB⊥BC，
∴∠ABC＝90°．
∴∠ABD＝180°﹣∠ABC﹣∠HBC＝α．
∵BE平分∠ABD，
∴∠DBE＝∠ABE＝α．
∵∠HBC＝90°﹣α，
∴∠DBC＝180°﹣∠HBC＝90°+α．
∵BF平分∠DBC，
∴∠DBF＝∠CBF＝∠DBC＝45°+α．
∴∠EBF＝∠DBF﹣∠DBE＝45°+α﹣α＝45°；
（3）∵∠BCN＝α，
∴∠HCB＝180°﹣∠BCN＝180°﹣α．
∵CF平分∠BCH，
∴∠BCF＝∠HCF＝∠HCB＝90°﹣α．
∵AM∥CN，
∴∠DFC＝∠HCF＝90°﹣α．
∵∠BFC＝3∠BCN，
∴∠BFC＝3α．
∴∠DFB＝∠DFC﹣∠BFC＝90°﹣α．
由（2）知：∠DBF＝45°+α．
∵BD⊥AM，
∴∠D＝90°．
∴∠DBF+∠DFB＝90°．
∴45°+α+90°﹣α＝90°．
解得：α＝15°．
∴∠FBC＝∠DBF＝45°+α＝52.5°．
∴∠EBC＝∠FBC+∠EBF＝52.5°+45°＝97.5°．
10．（邵东）点A、B在数轴上分别表示实数a、b，A、B两点之间的距离记作AB．当A、B两点中有一点为原点时，不妨设A点在原点．如图①所示，则AB＝OB＝|b|＝|a﹣b|．
当A、B两点都不在原点时：
（1）如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB﹣OA＝|b|﹣|a|＝b﹣a＝|b﹣a|＝|a﹣b|
（2）如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB﹣OA＝|b|﹣|a|＝﹣b﹣（﹣a）＝a﹣b＝|a﹣b|
（3）如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB+OA＝|b|+|a|＝a+（﹣b）＝|a﹣b|
回答下列问题：
（1）综上所述，数轴上A、B两点之间的距离AB＝ ．
（2）数轴上表示2和﹣4的两点A和B之间的距离AB＝ ．
（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝ | ，如果AB＝2，则x的值为 ．
（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为 ．
【答案】（1） AB＝|a﹣b|（2）6 （3）0或﹣4 （4）5
【解答】解：（1）综上所述，数轴上A、B两点之间的距离AB＝|a﹣b|；
（2）数轴上表示2和﹣4的两点A和B之间的距离AB＝2﹣（﹣4）＝2+4＝6；
（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝|x+2|，如果AB＝2，则x的值为0或﹣4；
（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为5．
故答案为：（1）|a﹣b|；（2）6；（3）|x+2|；0或﹣4；（4）5
11．（广安）点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB＝|a﹣b|，
例如：数轴上表示﹣1与﹣2的两点间的距离＝|﹣1﹣（﹣2）|＝﹣1+2＝1；
而|x+2|＝|x﹣（﹣2）|，所以|x+2|表示x与﹣2两点间的距离．
利用数形结合思想回答下列问题：
（1）数轴上表示﹣2和5两点之间的距离 ．
（2）若数轴上表示点x的数满足|x﹣1|＝3，那么x＝ ．
（3）若数轴上表示点x的数满足﹣4＜x＜2，则|x﹣2|+|x+4|＝ ．
【答案】（1）76（2） ﹣2或4（3）6
【解答】解：（1）根据题意知数轴上表示﹣2和5两点之间的距离为5﹣（﹣2）＝7，
故答案为：7；
（2）∵|x﹣1|＝3，即在数轴上到表示1和x的点的距离为3，
∴x＝﹣2或x＝4，
故答案为：﹣2或4；
（3）∵|x﹣2|+|x+4|表示在数轴上表示x的点到﹣4和2的点的距离之和，且x位于﹣4到2之间，
∴|x﹣2|+|x+4|＝2﹣x+x+4＝6，
故答案为：6．
12．（兴宁）如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是3个单位长度，长方形ABCD的长AD是6个单位长度，长方形EFGH的长EH是10个单位长度，点E在数轴上表示的数是5．且E、D两点之间的距离为14．
（1）填空：点H在数轴上表示的数是 ，点A在数轴上表示的数是 ．
（2）若线段AD的中点为M，线段EH上一点N，EN＝EH，M以每秒4个单位的速度向右匀速运动，N以每秒3个单位的速度向左运动，设运动时间为x秒，原点为O．当OM＝2ON时，求x的值．
（3）若长方形ABCD以每秒2个单位的速度向右匀速运动，长方形EFGH固定不动，设长方形ABCD运动的时间为t（t＞0）秒，两个长方形重叠部分的面积为S，当S＝12时，求此时t的值．
【答案】（1） 15；﹣15（2）或． （3）t的值为9或13．
【解答】解：（1）由题意可得，点H在数轴上表示的数为：5+10＝15；
点A在数轴上表示的数为：5﹣14﹣6＝﹣15．
故答案为：15；﹣15．
（2）∵点M是线段AD的中点，
∴点M表示的数为5﹣14﹣＝﹣12，
又∵EN＝EH，
∴点N在数轴上表示的数为：5+（15﹣5）＝，
由题意可得，x秒时，
点M在数轴上表示的数为：﹣12+4x，
点N在数轴上表示的数为：﹣3x，
∴OM＝|4x﹣12|，ON＝|3x﹣|，
∵OM＝2ON，
∴|4x﹣12|＝2|3x﹣|
∴4x﹣12＝2（3x﹣）或4x﹣12＝﹣2（3x﹣），
解得x＝或x＝．
故答案为：或．
（3）当CD与EF重合时，所用时间为＝7秒，
由题意得：AD与EH重合的部分为＝4，如图1所示，

设长方形ABCD从EF运动到AD与EH重叠部分为4时，所用的时间为t1秒，
∴t1＝＝2，
∴第一次重叠面积为12时，时间t为2+7＝9（秒）；
当AD与EH重叠部分为4时，如图2所示，
设长方形ABCD从EF运动到AD与EH重叠部分为4时，所用的时间为t2秒，
∴t2＝＝6，
∴第二次重叠面积S＝12时，时间t为6+7＝13（秒）；
∴当长方形ABCD与长方形EFGH重叠部分的面积为12时，t的值为9或13．
13．（宣化）如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示﹣，设点B所表示的数为m．
（1）实数m的值是 ；
（2）求|m+1|+|m﹣1|的值；
（3）在数轴上还有C、D两点分别表示实数c和d，且有|2c+d|与互为相反数，求2c﹣3d的平方根．
【答案】（1） 2﹣（2）2 （3）±4．
【解答】解：（1）m＝﹣+2＝2﹣；
（2）∵m＝2﹣，则m+1＞0，m﹣1＜0，
∴|m+1|+|m﹣1|＝m+1+1﹣m＝2；
答：|m+1|+|m﹣1|的值为2．
（3）∵|2c+d|与互为相反数，
∴|2c+d|+＝0，
∴|2c+d|＝0，且＝0，
解得：c＝﹣2，d＝4，或c＝2，d＝﹣4，
①当c＝﹣2，d＝4时，
所以2c﹣3d＝﹣16，无平方根．
②当c＝2，d＝﹣4时，
∴2c﹣3d＝16，
∴2c﹣3d的平方根为±4，
答：2c﹣3d的平方根为±4．
14．（锦江）阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．
当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；
当A、B两点都不在原点时，如图2，点A、B都在原点的右边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；
如图3，当点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；
如图4，当点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|．
回答下列问题：
（1）数轴上表示1和6的两点之间的距离是 数轴上表示2和﹣3的两点之间的距离是 ．
（2）数轴上若点A表示的数是x，点B表示的数是﹣4，则点A和B之间的距离是 ，若|AB|＝3，那么x为 ．
（3）当x是 时，代数式|x+2|+|x﹣1|＝7．
（4）若点A表示的数﹣1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒个单位长度，求运动几秒后，B、P、Q三点中，有一点恰好是另两点所连线段的中点？（请写出必要的求解过程）．
【答案】（1）5，5（2）﹣1或﹣7 （3）﹣4或3 （4）运动或或5秒
【解答】解：（1）数轴上表示1和6的两点之间的距离是|6﹣1|＝5，
数轴上表示2和﹣3的两点之间的距离是|2﹣（﹣3）|＝5．
（2）数轴上若点A表示的数是x，点B表示的数是﹣4，
则点A和B之间的距离是|x+4|，若|AB|＝3，
则|x+4|＝3，解得x＝﹣1或﹣7．
（3）当x＞1时，|x+2|+|x﹣1|＝x+2+x﹣1＝7，2x＝6，x＝3，
当x＜﹣2时，|x+2|+|x﹣1|＝﹣x﹣2+1﹣x＝7，﹣2x＝8，x＝﹣4，
当﹣2≤x≤1时，|x+2|+|x﹣1|＝x+2+1﹣x＝3≠7，∴当x＝﹣4或3时，代数式|x+2|+|x﹣1|＝7．
（4）设运动t秒后，有一点恰好是另两点所连线段的中点，由题意，得
①点B为线段PQ中点时，，解得，
②点P为线段BQ中点时，，解得，
③点Q为线段BP中点时，，解得t＝5．
答：运动或或5秒后，B、P、Q三点中，有一点恰好是另两点所连线段的中点．
15．（宣化）阅读下面的文字，解答问题．
大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能完全地写出来，于是小明用﹣1来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是1，用这个数减去其整数部分，差就是小数部分．
请解答下列问题：
（1）求出+2的整数部分和小数部分；
（2）已知：10+＝x+y，其中x是整数，且0＜y＜1，请你求出（x﹣y）的相反数．
【答案】（1）3，﹣1 （2）﹣14
【解答】解：（1）∵1＜＜2，
∴3＜+2＜4，
∴+2的整数部分是1+2＝3，+2的小数部分是﹣1；
（2）∵2＜＜3，
∴12＜10+＜13，
∴10+的整数部分是12，10+的小数部分是10+﹣12＝﹣2，
即x＝12，y＝﹣2，
∴x﹣y＝12﹣（﹣2）＝12﹣+2＝14﹣，
则x﹣y的相反数是﹣14．
16．（靖江）在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），则称点Q是点P的“a阶派生点”（其中a为常数，且a≠0）．例如：点P（1，4）的“2阶派生点”为点Q（2×1+4，1+2×4），即点Q（6，9）．
（1）若点P的坐标为（﹣1，5），则它的“3阶派生点”的坐标为 ；
（2）若点P的“5阶派生点”的坐标为（﹣9，3），求点P的坐标；
（3）若点P（c+1，2c﹣1）先向左平移2个单位长度，再向上平移1个单位长度后得到了点P1．点P1的“﹣4阶派生点”P2位于坐标轴上，求点P2的坐标．
【答案】（1）（2，14） （2）（﹣2，1）； （3）（0，﹣15）或（，0）．
【解答】解：（1）3×（﹣1）+5＝2；﹣1+3×5＝14，
∴点P的坐标为（﹣1，5），则它的“3级派生点”的坐标为（2，14）．
故答案为：（2，14）；
（2）设点P的坐标为（a，b），
由题意可知，
解得：，
∴点P的坐标为（﹣2，1）；
（3）由题意，P1（c﹣1，2c），
∴P1的“﹣4阶派生点“P2为：（﹣4（c﹣1）+2c，c﹣1﹣8c），即（﹣2c+4，﹣7c﹣1），
∵P2在坐标轴上，
∴﹣2c+4＝0或﹣7c﹣1＝0，
∴c＝2或c＝﹣，
∴P2（0，﹣15）或（，0）．
17．（黄山）在平面直角坐标系xOy中，对于P，Q两点给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P，Q两点为“等距点”．下图中的P，Q两点即为“等距点”．
（1）已知点A的坐标为（﹣3，1），
①在点E（0，3），F（3，﹣3），G（2，﹣5）中，为点A的“等距点”的是 ；
②若点B的坐标为B（m，m+6），且A，B两点为“等距点”，则点B的坐标为 ；
（2）若T1（﹣1，﹣k﹣3），T2（4，4k﹣3）两点为“等距点”，求k的值．
【答案】（1）①E、F；②（﹣3，3）； （2）1或2
【解答】解：（1）①∵点A（﹣3，1）到x、y轴的距离中最大值为3，
∴与A点是“等距点”的点是E、F．
②当点B坐标中到x、y轴距离其中至少有一个为3的点有（3，9）、（﹣3，3）、（﹣9，﹣3），
这些点中与A符合“等距点”的是（﹣3，3）．
故答案为①E、F；②（﹣3，3）；
（2）T1（﹣1，﹣k﹣3），T2（4，4k﹣3）两点为“等距点”，
①若|4k﹣3|≤4时，则4＝﹣k﹣3或﹣4＝﹣k﹣3
解得k＝﹣7（舍去）或k＝1．
②若|4k﹣3|＞4时，则|4k﹣3|＝|﹣k﹣3|
解得k＝2或k＝0（舍去）．
根据“等距点”的定义知，k＝1或k＝2符合题意．
即k的值是1或2．
18．（延长）在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．
（1）直接写出点B和点C的坐标B（ ， ）、C（ ， ）；
（2）当点P运动时，用含t的式子表示线段AP的长，并写出t的取值范围；
（3）点D（2，0），连接PD、AD，在（2）条件下是否存在这样的t值，使S△APD＝S四边形ABOC，若存在，请求出t值，若不存在，请说明理由．
【答案】（1）0、6，8、0 （2） AP＝8﹣2t（0≤t＜4）；AP＝2t﹣8（4≤t≤7）．
（3）当t为3秒和5秒时S△APD＝S四边形ABOC
【解答】解：（1）B（0，6），C（8，0），
故答案为：0、6，8、0；
（2）当点P在线段BA上时，
由A（8，6），B（0，6），C（8，0）可得：AB＝8，AC＝6
∵AP＝AB﹣BP，BP＝2t，
∴AP＝8﹣2t（0≤t＜4）；
当点P在线段AC上时，
∵AP＝点P走过的路程﹣AB＝2t﹣8（4≤t≤7）．
（3）存在两个符合条件的t值，
当点P在线段BA上时
∵S△APD＝AP•AC S四边形ABOC＝AB•AC
∴（8﹣2t）×6＝×8×6，
解得：t＝3＜4，
当点P在线段AC上时，
∵S△APD＝AP•CD CD＝8﹣2＝6
∴（2t﹣8）×6＝×8×6，
解得：t＝5＜7，综上所述：当t为3秒和5秒时S△APD＝S四边形ABOC，
19．（齐齐哈尔）如图①，在平面直角坐标系中，点A、B在x轴上，AB⊥BC，AO＝OB＝2，BC＝3
（1）写出点A、B、C的坐标．
（2）如图②，过点B作BD∥AC交y轴于点D，求∠CAB+∠BDO的大小．
（3）如图③，在图②中，作AE、DE分别平分∠CAB、∠ODB，求∠AED的度数．
【答案】（1） A（﹣2，0），B（2，0），C（2，3）；（2）90° （3）45°
【解答】解：（1）依题意得：A（﹣2，0），B（2，0），C（2，3）；
（2）∵BD∥AC，
∴∠ABD＝∠BAC，
∴CAB+∠BDO＝∠ABD+∠BDO＝90°；
（3）：∵BD∥AC，
∴∠ABD＝∠BAC，
∵AE，DE分别平分∠CAB，∠ODB，
∴∠CAE+∠BDE＝（∠BAC+∠BDO）＝（∠ABD+∠BDO）＝×90°＝45°，
过点E作EF∥AC，
则∠CAE＝∠AEF，∠BDE＝∠DEF，
∴∠AED＝∠AEF+∠DEF＝∠CAE+∠BDE＝45°．
20．（随县）如图，在平面直角坐标系中，已知点A（0，2），B（4，0），C（4，3）三点．
（1）求△ABC的面积；
（2）如果在第二象限内有一点P（m，1），且四边形ABOP的面积是△ABC的面积的两倍；求满足条件的P点坐标．
【答案】（1） 6（2） P（﹣8，1）
【解答】解：（1）∵B（4，0），C（4，3），
∴BC＝3，
∴S△ABC＝×3×4＝6；
（2）∵A（0，2）（4，0），
∴OA＝2，OB＝4，
∴S四边形ABOP＝S△AOB+S△AOP
＝×4×2+×2（﹣m）＝4﹣m，
又∵S四边形ABOP＝2S△ABC＝12，
∴4﹣m＝12，
解得：m＝﹣8，
∴P（﹣8，1）．