




所属成套资源:人教版数学八年级上册期末高分训练(原卷+解析)
人教版数学八上高分突破训练专项02 三角形综合能力提升训练(2份,原卷版+解析版)
展开
这是一份人教版数学八上高分突破训练专项02 三角形综合能力提升训练(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项02三角形综合能力提升训练原卷版doc、人教版数学八上高分突破训练专项02三角形综合能力提升训练解析版doc等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
A.50°B.60°C.70°D.80°
【答案】B
【解答】解:延长DC交AB于E,
∵∠BCD=∠B+∠CEB,∠BCD=110°,∠B=20°,
∴∠CEB=110°﹣20°=90°,
∵∠CEB=∠A+∠D,∠D=30°,
∴∠A=90°﹣30°=60°,
故选:B.
2.如图,在△ABC中,∠ACB=80°,点D在AB上,将△ABC沿CD折叠,点B落在边AC的点E处.若∠ADE=24°,则∠A的度数为( )
A.24°B.32°C.38°D.48°
【答案】C
【解答】解:∵∠ADE=24°,
∴∠BDE=180°﹣∠ADE=156°,
∵将△ABC沿CD折叠,点B落在边AC的点E处,
∴∠BCD=∠ACD,∠BDC=∠EDC=∠BDE==78°,
∵∠ACB=80°,
∴∠ACD=∠BCD=ACB=40°,
∴∠A=180°﹣∠ACD﹣∠ADE﹣∠CDE=180°﹣40°﹣78°﹣24°=38°,
故选:C.
3.如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,若∠A=45°,∠P=40°,则∠C的度数为( )
A.30°B.35°C.40°D.45°
【答案】B
【解答】解:∵∠A+∠ADG+∠AGD=180°,∠ABC+∠C+∠BGC=180°,
∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC.
又∵∠AGD=∠BGC,
∴∠A+∠ADG=∠C+∠GBC.
∴∠A﹣∠C=∠GBC﹣∠ADG.
同理可得,∠A+∠ADE=∠P+∠PBE.
∴∠A﹣∠P=∠PBE﹣∠ADE.
∵BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,
∴∠GBC=2∠PBE,∠ADG=2∠ADE.
∴∠A﹣∠C=2(∠A﹣∠P).
∴∠A+∠C=2∠P.
又∵∠A=45°,∠P=40°,
∴∠C=35°.
故选:B.
4.如图,已知AB∥DC,Rt△FEG直角顶点在CD上,已知∠FEC=35°,则∠GHB=( )
A.35°B.45°C.55°D.65°
【答案】C
【解答】解:∵∠FEG=90°,
∴∠GED+∠CEF=90°,
∵∠CEF=35°,
∴∠GED=55°,
∵AB∥CD,
∴∠GHB=∠GED=55°.
故选:C.
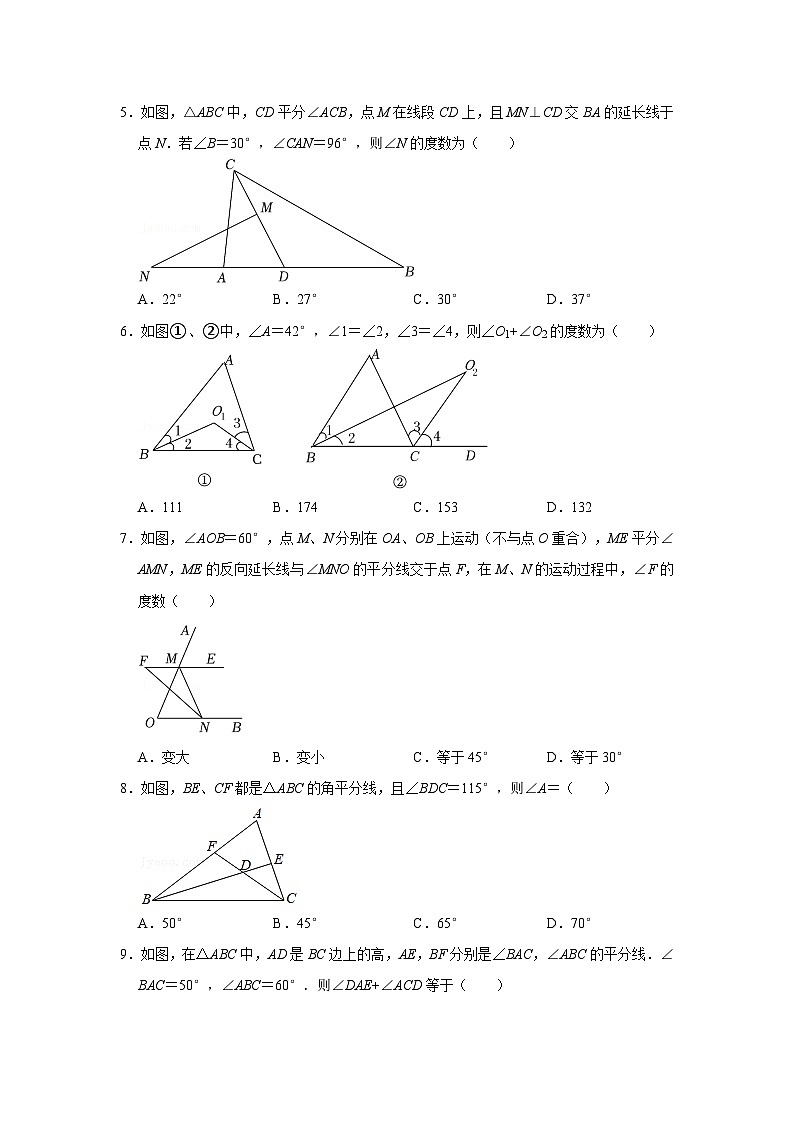
5.如图,△ABC中,CD平分∠ACB,点M在线段CD上,且MN⊥CD交BA的延长线于点N.若∠B=30°,∠CAN=96°,则∠N的度数为( )
A.22°B.27°C.30°D.37°
【答案】B
【解答】解:如图所示,∠NAC是三角形ABC的一个外角,
∴∠NAC=∠B+∠ACB,即∠ACB=∠NAC﹣∠B;
∵CD平分∠ACB,
∴∠ACD=∠DCB=∠ACB,
∵∠B=30°,∠CAN=96°,
∴∠ACD=∠ACB=(96°﹣30°)=33°,
∵MN⊥CD,
∴在直角三角形OMC中,
∠COM=90°﹣33°=57°,
∵∠NOA与∠COM互为对顶角,
∴∠NOA=∠COM=57°,
∴∠N=180°﹣57°﹣96°=27°.
故选:B.
6.如图①、②中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2的度数为( )
A.111B.174C.153D.132
【答案】D
【解答】解:∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣42°=138°.
∵∠1=∠2=∠ABC,∠3=∠4=∠ACB,
∴∠2+∠4=69°.
∵∠2+∠4+∠O1=180°,
∴∠O1=180°﹣69°=111°.
∵∠ACD=∠A+∠ABC=42°+∠ABC,
又∵∠1=∠2=∠ABC,∠3=∠4=∠ACD,
∴∠4=(42°+∠ABC)=21°+∠ABC.
∵∠4=∠2+∠O2.
∴∠O2=∠4﹣∠2
=21°+∠ABC﹣ABC
=21°
∴∠O1+∠O2=111°+21°=132°.
故选:D.
7.如图,∠AOB=60°,点M、N分别在OA、OB上运动(不与点O重合),ME平分∠AMN,ME的反向延长线与∠MNO的平分线交于点F,在M、N的运动过程中,∠F的度数( )
A.变大B.变小C.等于45°D.等于30°
【答案】D
【解答】解:∵∠AMN是△OMN的外角,
∴∠AMN=∠O+∠ONM,
∵∠EMN是△FMN的外角,
∴∠EMN=∠F+∠FNM,
∵ME平分∠AMN,FN平分∠MNO,
∴∠AMN=2∠EMN,∠ONM=2∠FNM,
∴∠O=2∠F,
∴∠F=30°.
故选:D.
8.如图,BE、CF都是△ABC的角平分线,且∠BDC=115°,则∠A=( )
A.50°B.45°C.65°D.70°
【答案】A
【解答】解:∵BE、CF都是△ABC的角平分线,
∴∠EBC=∠ABC,∠BCF=∠ACB.
∵∠EBC+∠FCB+∠BDC=180°,∠BDC=115°,
∴∠EBC+∠FCB=65°.
∴∠ABC+∠ACB=130°.
∵∠ABC+∠ACB+∠A=180°,
∴∠A=50°.
故选:A.
9.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线.∠BAC=50°,∠ABC=60°.则∠DAE+∠ACD等于( )
A.75°B.80°C.85°D.90°
【答案】A
【解答】解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°.
故选:A.
10.如图,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2021BC与∠A2021CD的平分线相交于点A2022,得∠A2022,则∠A2022是( )度.
A.xB.xC.xD.x
【答案】C
【解答】解:∵∠ACD是△ABC三角形的外角,∠A1CD是△A1BC的外角,
∴∠A=∠ACD﹣∠ABC,∠A1=∠A1CD﹣∠A1BC,
∵BA1和CA1分别是∠ABC和∠ACD的角平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1=∠ACD﹣∠ABC=∠A=x°,
同理可得,∠A2=∠A1=×x°,∠A3=∠A2=××x°,…,
∴∠A2022=x°,
故选:C.
11.如图,在△ABC中,∠C=90°,∠B=70°,点D、E分别在AB、AC上,将△ADE沿DE折叠,使点A落在点F处.则∠BDF﹣∠CEF=( )
A.20°B.30°C.40°D.50°
【答案】C
【解答】解:∵∠A+∠B+∠C=180°,∠C=90°,∠B=70°,
∴∠A=20°.
∵△DEF是由△DEA折叠成的,
∴∠1=∠2,∠3=∠DEF.
∵∠BDF+∠1+∠2=180°,
∴∠BDF=180°﹣2∠1.
∵∠CEF+∠CED=∠DEF=∠3,∠CED=∠1+∠A,∠3+∠1+∠A=180°,
∴∠3=180°﹣∠1﹣∠A.
∴∠CEF=∠3﹣∠CED.
=180°﹣∠1﹣∠A﹣∠1﹣∠A
=180°﹣2∠1﹣2∠A
=140°﹣2∠1.
∴∠BDF﹣∠CEF=180°﹣2∠1﹣(140°﹣2∠1)
=180°﹣2∠1﹣140°+2∠1
=40°.
故选:C.
12.如图,在△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,CH⊥AB于点H,则∠DCH的度数是( )
A.5°B.10°C.15°D.20°
【答案】A
【解答】解:在△ABC中,
∵∠A=60°,∠B=70°,
∴∠ACB=180°﹣∠A﹣∠B=50°.
∵CD是∠ACB的平分线,
∴∠ACD=∠ACB=25°.
∵CH⊥AB于点H,
∴∠CHB=90°.
∴∠ACH=∠CHB﹣∠A=30°.
∴∠DCH=∠ACH﹣∠ACD
=30°﹣25°
=5°.
故选:A.
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AC上一点,将△ABD沿线段BD翻折,使得点A落在A'处,若∠A'BC=30°,则∠CBD=( )
A.5°B.10°C.15°D.20°
【答案】C
【解答】解:∵∠ACB=90°,∠A=30°,
∴∠ABC=180°﹣∠ACB﹣∠A=60°,
由折叠性质得:∠ABD=∠A'BD,
∴∠ABC﹣∠CBD=∠A'BC+∠CBD,
∴60°﹣∠CBD=30°+∠CBD,
解得:∠CBD=15°.
故选:C.
14.如图,图①是四边形纸条ABCD,其中AB∥CD,E,F分别为AB、CD上的两个点,将纸条ABCD沿EF折叠得到图②,再将图②沿DF折叠得到图③,若在图③中,∠FEM=24°,则∠EFC为( )
A.48°B.72°C.108°D.132°
【答案】C
【解答】解:如图②,由折叠得:∠B'EF=∠FEM=24°,
∵AE∥DF,
∴∠EFM=24°,∠BMF=∠DME=48°,
∵BM∥CF,
∴∠CFM+∠BMF=180°,
∴∠CFM=180°﹣48°=132°,
由折叠得:如图③,∠MFC=132°,
∴∠EFC=∠MFC﹣∠EFM=132°﹣24°=108°,
故选:C.
15.如图,在△ABC中,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A的度数为( )
A.30°B.45°C.20°D.22.5°
【答案】A
【解答】解:∵∠ABC的平分线与∠ACE的平分线交于点D,
∴∠ABD=∠CBD,∠ACD=∠ECD,
∵∠ACE=∠A+∠ABC,
即∠ACD+∠ECD=∠ABD+∠CBD+∠A,
∴2∠ECD=2∠CBD+∠A,
∴∠A=2(∠ECD﹣∠CBD),
∵∠ECD=∠CBD+∠D,∠D=15°,
∴∠D=∠ECD﹣∠CBD=15°,
∴∠A=2×15°=30°.
故选:A.
16.如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,则∠A的度数为( )
A.50°B.60°C.65°D.75°
【答案】C
【解答】解:∵∠D=120°,
∴∠DBC+∠DCB=60°,
∵∠1+∠2=55°,
∴∠ABC+∠ACB=60°+55°=115°,
∴∠A=180°﹣115°=65°,
故选:C.
17.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为( )
A.15°B.20°C.25°D.30°
【答案】B
【解答】解:延长DC,与AB交于点E.
∵∠ACD是△ACE的外角,∠A=50°,
∴∠ACD=∠A+∠AEC=50°+∠AEC.
∵∠AEC是△BDE的外角,
∴∠AEC=∠ABD+∠D=∠ABD+10°,
∴∠ACD=50°+∠AEC=50°+∠ABD+10°,
整理得∠ACD﹣∠ABD=60°.
设AC与BP相交于O,则∠AOB=∠POC,
∴∠P+∠ACD=∠A+∠ABD,
即∠P=50°﹣(∠ACD﹣∠ABD)=20°.
故选:B.
二.填空题(共5小题)
18.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为 .
【答案】120°
【解答】解:如图,连接AA',
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=∠ABC,∠A'CB=∠ACB,
∵∠BA'C=120°,
∴∠A'BC+∠A'CB=180°﹣120°=60°,
∴∠ABC+∠ACB=120°,
∴∠BAC=180°﹣120°=60°,
∵沿DE折叠,
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°,
故答案为:120°.
19.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P= °.
【答案】30
【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,
故答案为:30°.
20.在△ABC中,∠ABC,∠ACB的平分线交于点O,∠ACB的外角平分线所在直线与∠ABC的平分线相交于点D,与∠ABC的外角平分线相交于点E,则下列结论一定正确的是 .(填写所有正确结论的序号)
①;②;③∠E=∠A;④∠E+∠DCF=90°+∠ABD.
【答案】①②④
【解答】解:∵∠ABC,∠ACB的平分线交于点O,
∴∠ABD=∠OBC=∠ABC,∠OCB=∠ACO=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣×(180°﹣∠A)=90°+∠A,故①正确,
∵CD平分∠ACF,
∴∠DCF=∠ACF,
∵∠ACF=∠ABC+∠A,∠DCF=∠OBC+∠D,
∴∠D=∠A,故②正确;
∵∠MBC=∠A+∠ACB,∠BCN=∠A+∠ABC,∠ACB+∠A+∠ABC=180°,
∴∠MBC+∠BCN=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∵BE平分∠MBC,CE平分∠BCN,
∴∠MBC=2∠EBC,∠BCN=2∠BCE,
∴∠EBC+∠BCE=90°+∠A,
∵∠E+∠EBC++BCE=180°,
∴∠E=180°﹣(∠EBC++BCE)=180°﹣(90°+∠A)=90°﹣∠A,故③错误;
∵∠DCF=∠DBC+∠D,
∴∠E+∠DCF=90°﹣∠A+∠DBC+∠A=90°+∠DBC,
∵∠ABD=∠DBC,
∴∠E+∠DCF=90°+∠ABD.故④正确,
综上正确的有:①②④.
21.用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC= 度.
【答案】36
【解答】解:∵∠ABC==108°,△ABC是等腰三角形,
∴∠BAC=∠BCA=36度.
22.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是 .
【答案】n2+2n
【解答】解:第一个是1×3,
第二个是2×4,
第三个是3×5,
…
第 n个是n•(n+2)=n2+2n
故答案为:n2+2n.
三.解答题(共8小题)
23.如图所示,D是△ABC边BC的中点,E是AD上一点,满足AE=BD=DC,FA=FE.求∠ADC的度数.
【解答】解:延长AD至G,使AD=DG,连接BG,在DG上截取DH=DC,
在△ADC和△GDB中,,
∴△ADC≌△GDB(SAS),
∴AC=BG,∠G=∠CAD,
∵FA=FE,
∴∠CAD=∠AEF,
∴∠G=∠CAD=∠AEF=∠BED,
∴BG=BE=AC,
∵AE=DC=BD,
∴AE+ED=DH+ED,
∴AD=EH,
在△DAC和△HEB中,
,
∴△DAC≌△HEB(SAS),
∴CD=BH,
∴BD=BH=DH,
∴△BDH为等边三角形,
∴∠C=∠BDH=60°=∠ADC.
故答案为:60°.
24.在△ABC中,AE平分∠BAC,∠C>∠B.
(1)课本原题再现:如图1,若AD⊥BC于点D,∠ABC=40°,∠ACB=60°,求∠EAD的度数. (写出解答过程)
(2)如图1,根据(1)的解答过程,猜想并写出∠B、∠C、∠EAD之间的数量关系.
(3)小明继续探究,如图2在线段AE上任取一点P,过点P作PD⊥BC于点D,请尝试写出∠B、∠C、∠EPD 之间的数量关系,并说明理由.
【解答】(1)先求出∠BAC,根据角平分线定义求出∠CAE,根据三角形内角和定理求出∠CAD,代入∠DAE=∠CAE﹣∠CAD求出即可;
(2)先利用三角形的内角和及角平分线的定义求得∠CAE=90°﹣(∠ABC+∠ACB),再根据直角三角形的性质可得∠CAD=90°﹣∠ACB,然后由∠EAD=∠CAE﹣∠CAD代入计算可求解;
(3)过A作AG⊥BC于G,由三角形的内角和定理及角平分线的定义可求得∠EAC=90°﹣∠ABC﹣∠ACB,再根据直角三角形的性质可得∠GAC=90°﹣∠ACB,进而可求解.
25.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.
【解答】解:(1)∵△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF,
∵∠B=50°,∠BAD=30°,
∴∠AFC=∠B+∠BAD+∠DAF=110°;
(2)∵∠B=50°,∠BAD=30°,
∴∠ADB=180°﹣50°﹣30°=100°,
∠ADC=50°+30°=80°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠ADE﹣∠ADC
=100°﹣80°=20°.
26.如图,将长方形纸片ABCD(四个内角均为直角,两组对边分别平行)沿EF折叠后,点C、D分别落在点M、N的位置,EN的延长线交BC于点G.
(1)若∠EFG=68°,求∠AEN、∠BGN的度数;
(2)若点P是射线BA上一点(点P不与点A重合),过点P作PH⊥EG于H,PQ平分∠APH,PQ与EF有怎样的位置关系?为什么?
【解答】解:(1)由折叠可知∠DEF=∠GEF,
∵AD∥BC,
∴∠EFG=∠DEF=68°,
∴∠AEN=180°﹣∠DEN=44°,
∴∠BGN=∠DEG=136°;
(2)PQ⊥EF或PQ∥EF;
①点P在线段AB上,PQ⊥EF,
如图,
设PQ交EF于点T,
∵PQ平分∠APH,
∴∠APQ=∠HPQ,
设∠APQ=∠HPQ=α,∠DEF=∠GEF=β,
由题意可知∠A=90°,
∵PH⊥EG,
∴∠PHE=90°,
在四边形APHE中,∠A+∠APH+∠PHE+∠AEH=360°
∴∠APH+∠AEG=180°,
∵∠AEG=180°﹣∠GED=180°﹣2β,
∴2α+180°﹣2β=180°,
∴α=β,
∵∠TEA=β,α+∠AKP=90°,∠AKP=∠TKE,
∴∠TKE+∠KET=90°,
∴∠KTE=90°,
∴PQ⊥EF;
②点P在线段BA的延长线上,PQ∥EF,
如图,
设PQ交EF于点T,
∵PQ平分∠APH,
∴∠APQ=∠HPQ,
设∠APQ=∠HPQ=α,∠DEF=∠GEF=β,
由题意可知∠ABC=90°,
在四边形APHE中,∠A+∠BPH+∠PHG+∠BGH=360°,
∴∠BGE+∠BFH=180°,
∵长方形纸片ABCD中,AD∥BC,
∴∠BGE=∠GED=2β,
∴2α+2β=180°,
∴α+β=90°,
∵α+∠PTE=90°,
∴β=∠ETP,
即∠GEF=∠ETP,
∴PQ∥EF,
综上所述:点P在线段AB上,PQ⊥EF;点P在线段BA的延长线上,PQ∥EF.
27.(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.
解:因为BD平分∠ABC(已知),
所以∠1= (角平分线定义).
同理:∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( ),
所以∠D= (等式性质).
即:∠D=90°+∠A.
(2)探究,请直接写出结果,并任选一种情况说明理由:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
【解答】解:(1)解:因为BD平分∠ABC(已知),
所以∠1=∠ABC (角平分线定义).
同理:∠2=∠ACB.
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( 三角形的内角和等于180° ),
所以∠D=180°﹣(∠ABC+∠ACB) (等式性质).
即:∠D=90°+∠A.
故答案为:ABC,ACB,三角形的内角和等于180°,180°﹣(∠ABC+∠ACB).
(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A+2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
(ii)∠D与∠A之间的等量关系是:∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即:∠D=∠A.
故答案为:∠D=∠A.
28.如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=75°,∠ACB=45°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
【解答】解:∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE﹣∠DBC),∠D=∠DCE﹣∠DBC,
∴∠A=2∠D,
∵∠ABC=75°,∠ACB=45°,
∴∠A=60°,
∴∠D=30°;
(2)∠D=(∠M+∠N﹣180°);
理由:延长BM、CN交于点A,
则∠A=∠BMN+∠CNM﹣180°,
由(1)知,∠D=A,
∴∠D=(∠M+∠N﹣180°).
29.a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为18,求c的值.
【解答】解:(1)∵a,b,c分别为△ABC的三边,a+b=3c﹣2,a﹣b=2c﹣6,
∴,
解得:1<c<6;
(2)∵△ABC的周长为18,a+b=3c﹣2,
∴a+b+c=4c﹣2=18,
解得c=5.
30.问题情景 如图1,△ABC中,有一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.
试问∠ABP与∠ACP是否存在某种确定的数量关系?
(1)特殊探究:若∠A=50°,则∠ABC+∠ACB= 度,∠PBC+∠PCB= 度,∠ABP+∠ACP= 度;
(2)类比探索:请探究∠ABP+∠ACP与∠A的关系.
(3)类比延伸:如图2,改变直角三角板PMN的位置;使P点在△ABC外,三角板PMN的两条直角边PM、PN仍然分别经过点B和点C,(2)中的结论是否仍然成立?若不成立,请直接写出你的结论.
【解答】解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP=130°﹣90°=40°.
故答案为:130,90,40;
(2)结论:∠ABP+∠ACP=90°﹣∠A.
证明:∵90°+(∠ABP+∠ACP)+∠A=180°,
∴∠ABP+∠ACP+∠A=90°,
∴∠ABP+∠ACP=90°﹣∠A.
(3)不成立; 存在∠ACP﹣∠ABP=90°﹣∠A.
理由:△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABC+∠ACB)﹣(∠PBC+∠PCB)=180°﹣∠A﹣90°,
即∠ABC+∠ACP+∠PCB﹣∠ABP﹣∠ABC﹣∠PCB=90°﹣∠A,
∴∠ACP﹣∠ABP=90°﹣∠A.
相关试卷
这是一份人教版数学八上高分突破训练专项14 等腰三角形分类讨论问题综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项14等腰三角形分类讨论问题综合应用原卷版doc、人教版数学八上高分突破训练专项14等腰三角形分类讨论问题综合应用解析版doc等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
这是一份人教版数学八上高分突破训练专项13 与尺规作图有关的计算和证明的综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项13与尺规作图有关的计算和证明的综合应用原卷版doc、人教版数学八上高分突破训练专项13与尺规作图有关的计算和证明的综合应用解析卷doc等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
这是一份人教版数学八上高分突破训练专项08 对角互补模型综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项08对角互补模型综合应用原卷版doc、人教版数学八上高分突破训练专项08对角互补模型综合应用解析版doc等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。










