人教版数学八上高分突破训练专项08 对角互补模型综合应用（2份，原卷版+解析版）

这是一份人教版数学八上高分突破训练专项08 对角互补模型综合应用（2份，原卷版+解析版），文件包含人教版数学八上高分突破训练专项08对角互补模型综合应用原卷版doc、人教版数学八上高分突破训练专项08对角互补模型综合应用解析版doc等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

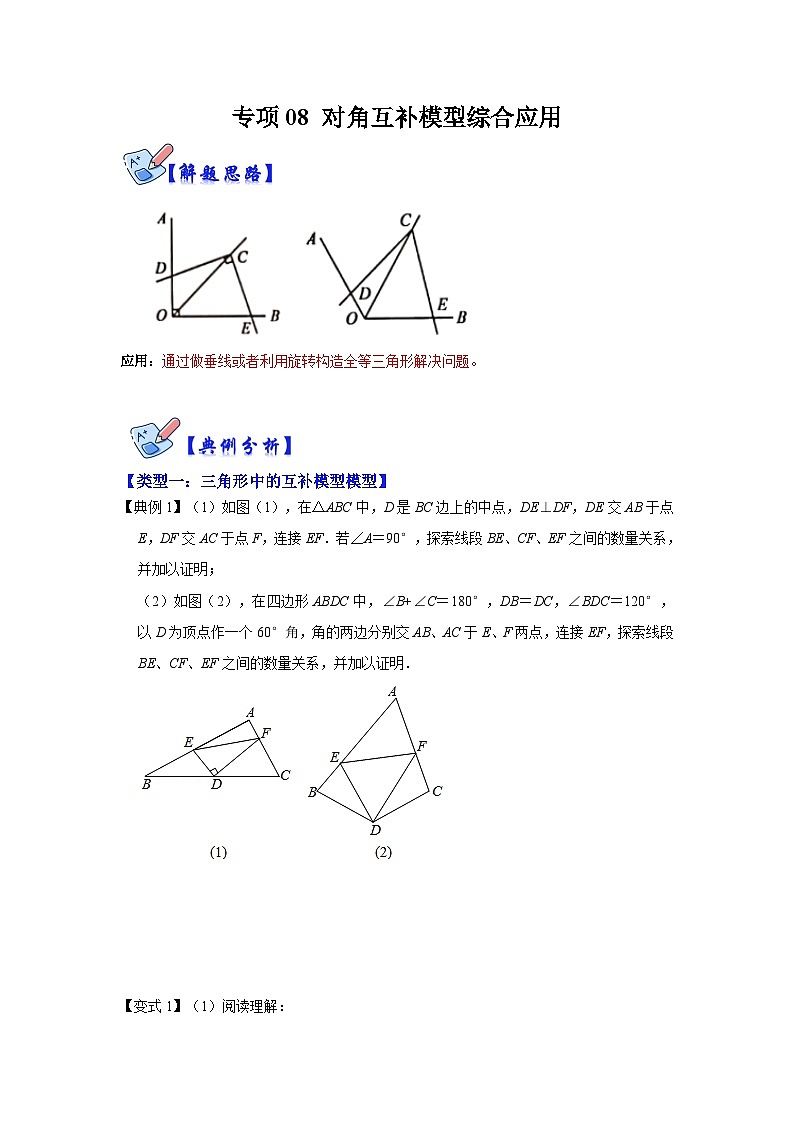
应用：通过做垂线或者利用旋转构造全等三角形解决问题。
【类型一：三角形中的互补模型模型】
【典例1】（1）如图（1），在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．若∠A＝90°，探索线段BE、CF、EF之间的数量关系，并加以证明；
（2）如图（2），在四边形ABDC中，∠B+∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．
【解答】证明：（1）EF2＝BE2+CF2，
理由如下：如图（1）延长ED到G，使DG＝ED，连接CG，FG，
在△DCG与△DBE中，
，
∴△DCG≌△DBE（SAS），
∴DG＝DE，CG＝BE，∠B＝∠DCG，
又∵DE⊥DF，
∴FD垂直平分线段EG，
∴FG＝FE，
∵∠A＝90°，
∴∠B+∠ACB＝90°，
∴∠FCG＝90°，
在△CFG中，CG2+CF2＝FG2，
∴EF2＝BE2+CF2；
（2）如图（2），结论：EF＝EB+FC，
理由如下：延长AB到M，使BM＝CF，
∵∠ABD+∠C＝180°，又∠ABD+∠MBD＝180°，
∴∠MBD＝∠C，
在△BDM和△CDF中，
，
∴△BDM≌△CDF（SAS），
∴DM＝DF，∠BDM＝∠CDF，
∴∠EDM＝∠EDB+∠BDM＝∠EDB+∠CDF＝∠CDB﹣∠EDF＝120°﹣60°＝60°＝∠EDF，
在△DEM和△DEF中，
，
∴△DEM≌△DEF（SAS），
∴EF＝EM，
∴EF＝EM＝BE+BM＝EB+CF．
【变式1】（1）阅读理解：
如图①，在△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：
延长AD到点E使DE＝AD，再连接BE，这样就把AB，AC，2AD集中在△ABE中，利用三角形三边的关系可判断线段AE的取值范围是 ；则中线AD的取值范围是 ；
（2）问题解决：
如图②，在△ABC中，D是BC边的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，此时：BE+CF EF（填“＞”或“＝”或“＜”）；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D＝180，CB＝CD，∠BCD＝140°，以C为顶点作∠ECF＝70°，边CE，CF分别交AB，AD于E，F两点，连接EF，此时：BE+DF EF（填“＞”或“＝”或“＜“）；
（4）若在图③的四边形ABCD中，∠ECF＝α（0°＜α＜90°），∠B+∠D＝180，CB＝CD，且（3）中的结论仍然成立，则∠BCD＝ （用含α的代数式表示）.
【解答】解：（1）在△ADC与△EDB中，
，
∴△ADC≌△EDB（SAS），
∴BE＝AC＝3，
在△ABE中，AB﹣BE＜AE＜AB+BE，
即2＜AE＜8，
∴2＜2AD＜8，
∴1＜AD＜4，
故答案为：2＜AE＜8；1＜AD＜4；
（2）如图，延长FD至点G，使DG＝DF，连接BG，EG，
∵点D是BC的中点，
∴DB＝DC，
∵∠BDG＝∠CDF，DG＝DF，
∴△BDG≌△CDF（SAS），
∴BG＝CF，
∵ED⊥FD，FD＝GD，
∴EF＝EG，
在△BEG中，BE+BG＞EG，
∴BE+CF＞EF，
故答案为：＞；
（3）BE+DF＝EF，
如图，延长AB至点G，使BG＝DF，连接CG，
∵∠ABC+∠D＝180°，∠ABC+∠CBG＝180°，
∴∠CBG＝∠D，
又∵CB＝CD，BG＝DF，
∴△CBG≌△CDF（SAS），
∴CG＝CF，∠BCG＝∠DCF，
∵∠BCD＝140°，∠ECF＝70°，
∴∠DCF+∠BCE＝70°，
∴∠BCE+∠BCG＝70°，
∴∠ECG＝∠ECF＝70°，
又∵CE＝CE，CG＝CF，
∴△ECG≌△ECF（SAS），
∴EG＝EF，
∵BE+BG＝EG，
∴BE+DF＝EF，
故答案为：＝；
（4）由（3）同理可得△CBG≌△CDF，
∴CG＝CF，∠BCG＝∠DCF，
若BE+DF＝EF，
则EG＝EF，
∴△ECF≌△ECG（SSS），
∴∠ECG＝∠ECF，
∴∠BCD＝2∠ECF＝2α，
故答案为：2α．
【类型二：四边形中的互补模型】
【典例2】（1）如图1，四边形ABCD是边长为5 cm的正方形，E，F分别在AD，CD边上，∠EBF＝45°．为了求出△DEF的周长．小南同学的探究方法是：
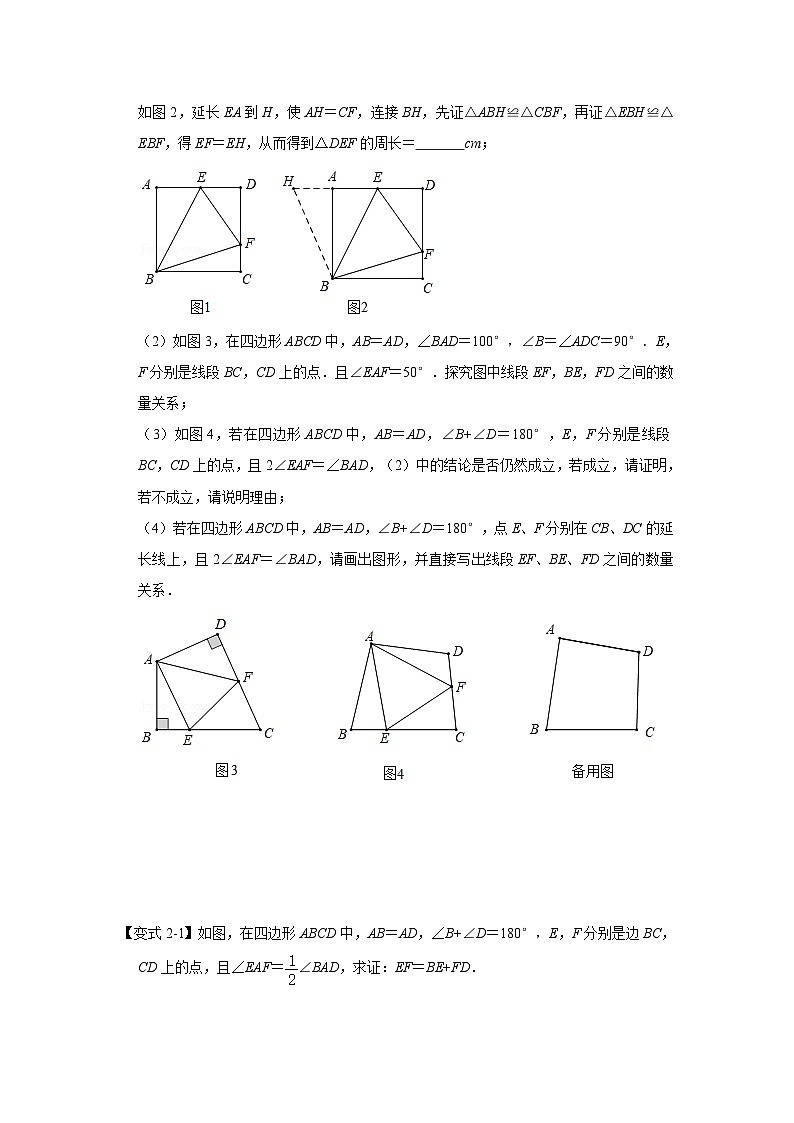
如图2，延长EA到H，使AH＝CF，连接BH，先证△ABH≌△CBF，再证△EBH≌△EBF，得EF＝EH，从而得到△DEF的周长＝ cm；
（2）如图3，在四边形ABCD中，AB＝AD，∠BAD＝100°，∠B＝∠ADC＝90°．E，F分别是线段BC，CD上的点．且∠EAF＝50°．探究图中线段EF，BE，FD之间的数量关系；
（3）如图4，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是线段BC，CD上的点，且2∠EAF＝∠BAD，（2）中的结论是否仍然成立，若成立，请证明，若不成立，请说明理由；
（4）若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别在CB、DC的延长线上，且2∠EAF＝∠BAD，请画出图形，并直接写出线段EF、BE、FD之间的数量关系．
【解答】解：（1）如图1，延长EA到H，使AH＝CF，连接BH，
∵四边形ABCD是正方形，
∴AB＝BC＝AD＝CD＝5cm，∠BAD＝∠BCD＝90°，
∴∠BAH＝∠BCF＝90°，
又∵AH＝CF，AB＝BC，
∴△ABH≌△CBF（SAS），
∴BH＝BF，∠ABH＝∠CBF，
∵∠EBF＝45°，
∴∠CBF+∠ABE＝45°＝∠HBA+∠ABE＝∠EBF，
∴∠EBH＝∠EBF，
又∵BH＝BF，BE＝BE，
∴△EBH≌△EBF（SAS），
∴EF＝EH，
∴EF＝EH＝AE+CF，
∴△DEF的周长＝DE+DF+EF＝DE+DF+AE+CF＝AD+CD＝10（cm）．
故答案为：10．
（2）EF＝BE+DF．
证明：如图2所示，延长FD到点G．使DG＝BE．连接AG，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠BAD＝100°，∠EAF＝50°，
∴∠BAE+∠FAD＝∠DAG+∠FAD＝50°，
∴∠EAF＝∠FAG＝50°，
在△EAF和△GAF中，
，
∴△EAF≌△GAF（SAS），
∴EF＝FG＝DF+DG，
∴EF＝BE+DF；
（3）成立．
证明：如图3，延长EB到G，使BG＝DF，连接AG．
∵∠ABC+∠D＝180°，∠ABG+∠ABC＝180°，
∴∠ABG＝∠D，
∵在△ABG与△ADF中，
，
∴△ABG≌△ADF（SAS），
∴AG＝AF，∠BAG＝∠DAF，
∵2∠EAF＝∠BAD，
∴∠DAF+∠BAE＝∠BAG+∠BAE＝∠BAD＝∠EAF，
∴∠GAE＝∠EAF，
又AE＝AE，
∴△AEG≌△AEF（SAS），
∴EG＝EF，
∵EG＝BE+BG，
∴EF＝BE+FD；
（4）EF＝DF﹣BE，
理由如下：在DF上截取DH，使DH＝BE，
∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，
∴∠ABE＝∠ADH，且AB＝AD，DH＝BE，
∴△ABE≌△ADH（SAS），
∴∠BAE＝∠DAH，AH＝AE，
∵∠EAF＝∠BAD，
∴∠DAH+∠BAF＝∠BAD，
∴∠HAF＝∠BAD＝∠EAF，且AF＝AF，AE＝AH，
∴△FAH≌△FAE（SAS），
∴HF＝EF，
∴EF＝HF＝DF﹣DH＝DF﹣BE
【变式2-1】如图，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是边BC，CD上的点，且∠EAF＝∠BAD，求证：EF＝BE+FD．
【解答】证明：延长CB至M，使BM＝FD，连接AM，如图所示：
∵∠ABC+∠D＝180°，∠ABM+∠ABC＝180°，
∴∠ABM＝∠D，
在△ABM与△ADF中，
，
∴△ABM≌△ADF（SAS），
∴AF＝AM，∠BAM＝∠DAF，
∵∠EAF＝∠BAD，
∴∠DAF+∠BAE＝∠BAD＝∠FAE，
∴∠BAM+∠BAE＝∠EAF，
即∠MAE＝∠EAF，
在△AME与△AFE中，
，
∴△AME≌△AFE（SAS），
∴EF＝ME，
∵ME＝BE+BM，
∴EF＝BE+FD．
【变式2-2】“截长补短法”证明线段的和差问题：
先阅读背景材料，猜想结论并填空，然后做问题探究．
背景材料：
（1）如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系．探究的方法是，延长FD到点G．使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出的结论是 ．
探索问题：
（2）如图2，若四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？成立的话，请写出推理过程．
【解答】证明：（1）在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝∠BAD，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△AGF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF；
故答案为：EF＝BE+DF．
（2）解：结论EF＝BE+DF仍然成立；
理由：延长FD到点G．使DG＝BE．连接AG，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝∠BAD，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△AGF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF．
1．阅读理解：
课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE＝AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．
感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
（1）问题解决：
受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
①求证：BE+CF＞EF；
②若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明；
（2）问题拓展：
如图3，在四边形ABDC中，∠B+∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．
【解答】解：①延长FD到G，使得DG＝DF，连接BG、EG．（或把△CFD绕点D逆时针旋转180°得到△BGD），
∴CF＝BG，DF＝DG，
∵DE⊥DF，
∴EF＝EG．
在△BEG中，BE+BG＞EG，即BE+CF＞EF．（4分）
②若∠A＝90°，则∠EBC+∠FCB＝90°，
由①知∠FCD＝∠DBG，EF＝EG，
∴∠EBC+∠DBG＝90°，即∠EBG＝90°，
∴在Rt△EBG中，BE2+BG2＝EG2，
∴BE2+CF2＝EF2；（3分）
（2）将△DCF绕点D逆时针旋转120°得到△DBG．
∵∠C+∠ABD＝180°，∠4＝∠C，
∴∠4+∠ABD＝180°，
∴点E、B、G在同一直线上．
∵∠3＝∠1，∠BDC＝120°，∠EDF＝60°，
∴∠1+∠2＝60°，故∠2+∠3＝60°，即∠EDG＝60°
∴∠EDF＝∠EDG＝60°，
∵DE＝DE，DF＝DG，
∴△DEG≌△DEF，
∴EF＝EG＝BE+BG，即EF＝BE+CF．（4分）
2．如图，△ABC中，AB＝AC，点D为△ABC内一点，其中AD平分∠BAC且∠CBD＝30°，点E为AC中点，EF⊥AC交BD延长线于点F，连接AF、CF．
（1）求∠ADF的大小；
（2）求证：△ACF是等边三角形；
（3）猜想AD、BD、DF的数量关系并说明理由．
【解答】解：（1）延长AD交BC于点M，
∵AB＝AC，AD平分∠BAC，
∴AM⊥BC，
∵∠CBD＝30°，
∴∠BDM＝90°﹣∠CBD＝60°，
∴∠ADF＝∠BDM＝60°；
（2）由（1）知∠ADC＝∠BDC＝120°，
∵∠ADF＝60°，
∴∠CDF＝60°，
过点F作FG⊥AD于点G，FH⊥DC于点H，
∴FG＝FH，
∵EF⊥AC，E为AC的中点，
∴AF＝CF，
在Rt△AGF和Rt△CHF中，
，
∴Rt△AGF≌Rt△CHF（HL），
∴∠AFG＝∠CFH，
∵∠DGF＝∠H＝90°，∠DGF+∠H+∠GDH+∠GFH＝360°，
∴∠GDH+∠GFH＝180°，
∵∠GDH＝120°，
∴∠GFH＝60°，
∴∠AFC＝∠AFG+∠GFC＝∠CFH+∠GFC＝60°，
又∵AF＝CF，
∴△ACF为等边三角形；
（3）DF＝AD+BD．
理由：在BF上截取PF＝BD，连接AP，
∵△ACF为等边三角形，
∴AF＝AC，
又∵AF＝AC，
∴AB＝AF，
∴∠ABD＝∠AFP，
∴△ABD≌△AFP（SAS），
∴AD＝AP，
又∵∠ADP＝60°，
∴△ADP为等边三角形，
∴AD＝DP，
∴DF＝DP+PF＝AD+BD．
3．（1）问题背景．
如图1，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是线段BC、线段CD上的点．若∠BAD＝2∠EAF，试探究线段BE、EF、FD之间的数量关系．
小明同学探究此问题的方法是，延长FD到点G．使DG＝BE．连接AG，先证明△ABE≌△ADG．再证明△AEF≌△AGF，可得出结论，他的结论应是 ．
（2）猜想论证．
如图2，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E在线段BC上、F在线段CD延长线上．若∠BAD＝2∠EAF，上述结论是否依然成立？若成立说明理由；若不成立，试写出相应的结论并给出你的证明．
【解答】解：延长FD到点G．使DG＝BE，连接AG，
∵∠B+∠ADF＝180°，∠ADF+∠ADG＝180°，
∴∠ADG＝∠B，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠BAD＝2∠EAF，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△AGF中，
，
∴△AEF≌△AGF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF；
故答案为：EF＝BE+DF．
（2）结论EF＝BE+FD不成立，结论：EF＝BE﹣FD．
理由如下：证明：如图2中，在BE上截取BG，使BG＝DF，连接AG．
∵∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，
∴∠B＝∠ADF．
∵在△ABG与△ADF中，
，
∴△ABG≌△ADF（SAS）．
∴∠BAG＝∠DAF，AG＝AF．
∴∠BAD＝∠BAG+∠GAD＝∠DAF+∠GAD＝∠GAF．
∵∠BAD＝2∠EAF，
∴∠GAF＝2∠EAF，
∴∠GAE＝∠EAF．
∵AE＝AE，
∴△AEG≌△AEF（SAS）．
∴EG＝EF
∵EG＝BE﹣BG
∴EF＝BE﹣FD
4．通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边DC、BC上，∠EAF＝45°，连接EF，试猜想EF、BF、DE之间的数量关系．
（1）思路梳理
把△ADE绕点A顺时针旋转90°至△ABG，可使AD与AB重合，由∠ABG＝∠D＝90°，得∠FBG＝180°，即点F、B、G共线，易证△AFG≌ ，故EF、BF、DE之间的数量关系为 ．
（2）类比引申
如图②，在四边形ABCD中，AB＝AD，∠ABC＝∠ADC＝90°．E、F分别是DC、BC上的点．且∠EAF＝∠BAD．猜想图中线段BF、EF、DE之间的数量关系 ．
（3）拓展提高
如图③，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且∠EAF＝∠BAD，探究上述结论是否仍然成立？说明理由．
【解答】解：（1）思路梳理：
如图①，把△ADE绕点A顺时针旋转90°至△ABG，可使AD与AB重合，即AB＝AD，
由旋转得：∠ABG＝∠D＝90°，DE＝BG，∠1＝∠2，AE＝AG，
∴∠FBG＝∠ABF+∠ABG＝90°+90°＝180°，
即点F、B、G共线，
∵四边形ABCD为正方形，
∴∠BAD＝90°，
∵∠EAF＝45°，
∴∠DAE+∠B＝∠FAG＝45°，
∴∠EAF＝∠FAG＝45°，
在△AFE和△AFG中，，
∴△AFE≌△AFG（SAS），
∴EF＝FG，
∴EF＝BF+BG＝BF+DE；
故答案为：△AFE，EF＝BF+DE；
（2）类比引申
如图②，把△ADE绕点A顺时针旋转90°至△ABG，可使AD与AB重合，即AB＝AD，
由旋转得：∠ABG＝∠D＝90°，DE＝BG，∠GAB＝∠DAE，AE＝AG，
∴∠FBG＝∠ABF+∠ABG＝90°+90°＝180°，
即点F、B、G共线，
∵∠EAF＝∠BAD，
∴∠DAE+∠BAF＝BAD，
∴∠GAF＝∠EAF，
在△AFE和△AFG中，，
∴△AFE≌△AFG（SAS），
∴EF＝FG，
∴EF＝BF+BG＝BF+DE；
（3）拓展提高
结论DE+BF＝EF仍然成立，
理由如下：如图③，将△ADE绕点A顺时针旋转90°得到△ABH，
由旋转可得，AH＝AE，BH＝DE，∠1＝∠2，
∵∠EAF＝∠DAB，
∴∠HAF＝∠1+∠3＝∠2+∠3＝∠BAD，
∴∠HAF＝∠EAF，
∵∠ABH+∠ABF＝∠D+∠ABF＝180°，
∴点H、B、F三点共线，
在△AEF和△AHF中，
∴△AEF≌△AHF（SAS），
∴EF＝HF，
∵HF＝BH+BF，
∴EF＝DE+BF．
5．如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．
（1）提示：探究此问题的方法是延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF．请根据提示按照提示的方法完成探究求解过程．
（2）探索延伸：
如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？ （成立或不成立）
（3）实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间夹角为70°，试求此时两舰艇之间的距离．
【解答】解：（1）EF＝BE+DF．理由如下：
如图1，延长FD到G，使DG＝BE，连接AG，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝∠BAD，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△GAF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF；
（2）EF＝BE+DF仍然成立．
证明：如图2，延长FD到G，使DG＝BE，连接AG，
∵∠B+∠ADC＝180°，∠ADC+∠ADG＝180°，
∴∠B＝∠ADG，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝∠BAD，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△GAF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF；
故答案是：成立；
（3）如图3，连接EF，延长AE、BF相交于点C，
∵∠AOB＝30°+90°+（90°﹣70°）＝140°，∠EOF＝70°，
∴∠EOF＝∠AOB，
又∵OA＝OB，
∠OAC+∠OBC＝（90°﹣30°）+（70°+50°）＝180°，
∴符合探索延伸中的条件，
∴结论EF＝AE+BF成立，
即EF＝1.5×（60+80）＝210（海里）．
答：此时两舰艇之间的距离是210海里．
6．在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，∠BCD＝120°，现将一个30°角的顶点落在点A处．
（1）如图①，当该角的两边分别与BC、CD边相交于E、F时．求证：EF＝BE+DF；
（2）现在将该角绕点A进行旋转，其两边分别与BC、CD边的延长线相交于点F，那么（1）中的结论是否仍然成立？若成立，说明理由；若不成立，试探究线段BE与DF之间的等量关系，并加以证明．（利用图②进行探索）
【解答】解：（1）如图①，
延长CB到H点，使BH＝DF，连接AH，
∵∠B＝∠D＝90°，∠BCD＝120°，
∴∠D+∠B＝180°，
∵∠ABE+∠ABH＝180°，
∴∠ABH＝∠D，
∵AD＝AB，BH＝DF，
∴在△ABH和△ADF中，
，
∴△ABH≌△ADF（SAS），
∴AH＝AF，∠HAB＝∠FAD，
∵∠DAB＝60°，∠FAE＝30°，
∴∠FAD+∠BAE＝30°，
∴∠BAE+∠HAB＝30°，即∠HAE＝30°，
在△HAE和△EAF中，
，
∴△HAE≌△FAE（SAS），
∴HE＝EF，
∵HE＝HB+BE＝DF+BE，
∴EF＝BE+DF；
（2）（1）中的结论不成立，
如图②，在BC上截取BH＝DF，
在△ABH与△ADF中，
，
∴△ABH≌△ADF，
∴∠BAH＝∠DAF，AH＝AF，
∴∠EAF＝30°，
∴∠BAH+∠EAD＝30°，
∵∠B＝∠D＝90°，∠BCD＝120°，
∴∠BAD＝60°，
∴∠HAE＝30°，
在△HAE与△FAE中，
，
∴△HAE≌△FAE，
∴HE＝EF，
∵BE＝BH+HE，
∴BE＝DF+EF．
7．【初步探索】
（1）如图1：在四边形ABCD中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；
【灵活运用】
（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；
【拓展延伸】
（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．
【解答】解：（1）∠BAE+∠FAD＝∠EAF．理由：
如图1，延长FD到点G，使DG＝BE，连接AG，
根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，
再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．
故答案为：∠BAE+∠FAD＝∠EAF；
（2）仍成立，理由：
如图2，延长FD到点G，使DG＝BE，连接AG，
∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，
∴∠B＝∠ADG，
又∵AB＝AD，
∴△ABE≌△ADG（SAS），
∴∠BAE＝∠DAG，AE＝AG，
∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，
∴△AEF≌△AGF（SSS），
∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；
（3）∠EAF＝180°﹣∠DAB．
证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，
∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，
∴∠ADC＝∠ABE，
又∵AB＝AD，
∴△ADG≌△ABE（SAS），
∴AG＝AE，∠DAG＝∠BAE，
∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，
∴△AEF≌△AGF（SSS），
∴∠FAE＝∠FAG，
∵∠FAE+∠FAG+∠GAE＝360°，
∴2∠FAE+（∠GAB+∠BAE）＝360°，
∴2∠FAE+（∠GAB+∠DAG）＝360°，
即2∠FAE+∠DAB＝360°，
∴∠EAF＝180°﹣∠DAB．