人教版数学八上高分突破训练专项11 用截长补短法构造全等三角形综合应用（2份，原卷版+解析版）

这是一份人教版数学八上高分突破训练专项11 用截长补短法构造全等三角形综合应用（2份，原卷版+解析版），文件包含人教版数学八上高分突破训练专项11用截长补短法构造全等三角形综合应用原卷版doc、人教版数学八上高分突破训练专项11用截长补短法构造全等三角形综合应用解析版doc等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
截长补短法原理：
截长：1.过某一点作长边的垂线；2.在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。
补短：1.延长短边；2.通过旋转等方式使两短边拼合到一起
延长边上（不一定是底边）的中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则 对应角 对应边都对应相等。 此法常用于构造 全等三角形 ，利用中线的性质、 辅助线 、 对顶角 一般用“ SAS ”证明对应边之间的关系。 （在一定范围中）
【典例1】（2020秋•富县期末）如图，AD是△ABC的角平分线，AB＞AC，求证：AB﹣AC＞BD﹣CD．
【变式1】（2020秋•顺庆区校级期中）如图：锐角△ABC中，∠C＝2∠B，AD是高，求证：AC+CD＝BD．
【变式2】如图所示，在△ABC中，∠1＝∠2，AB＝AC+CD．试判断∠B与∠C之间的关系．
【典例2】把两个全等的直角三角板的斜边重合，组成一个四边形ACBD以D为顶点作∠MDN，交边AC、BC于M、N．
（1）若∠ACD＝30°，∠MDN＝60°，当∠MDN绕点D旋转时，AM、MN、BN三条线段之间有何种数量关系？证明你的结论；
（2）当∠ACD+∠MDN＝90°时，AM、MN、BN三条线段之间有何数量关系？证明你的结论；
（3）如图③，在（2）的条件下，若将M、N改在CA、BC的延长线上，完成图3，其余条件不变，则AM、MN、BN之间有何数量关系（直接写出结论，不必证明）
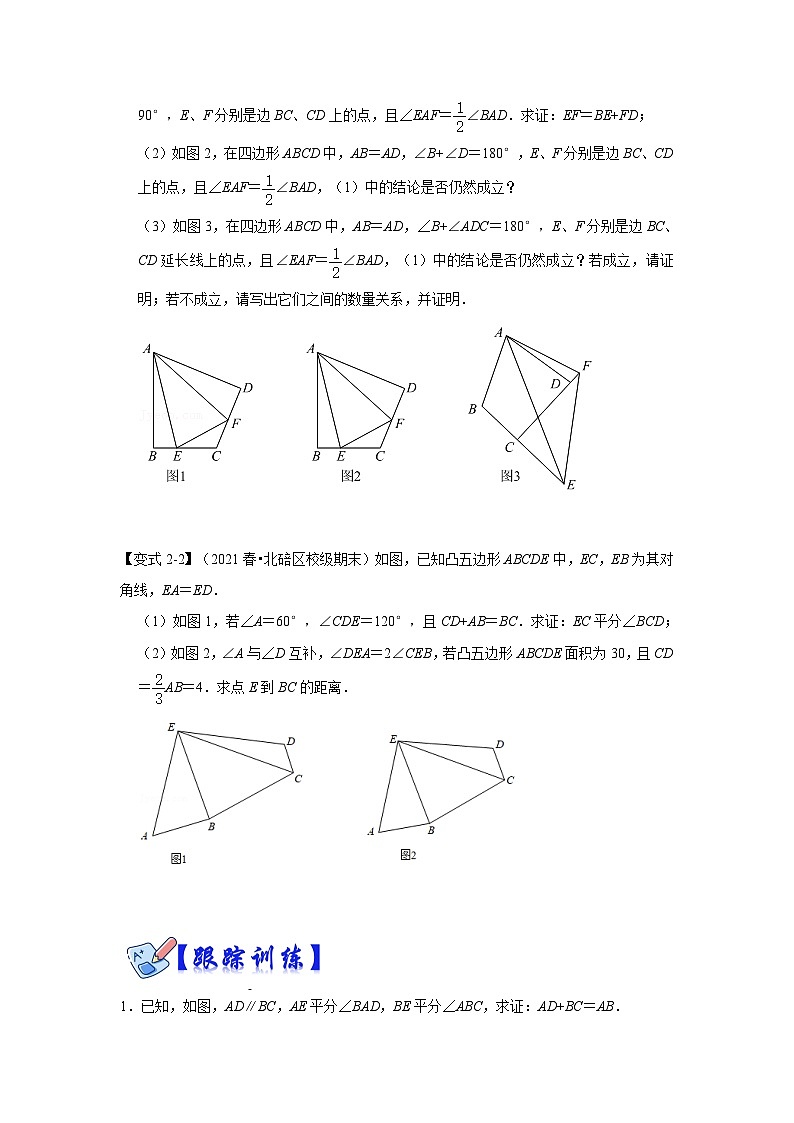
【变式2-1】（2012•昌平区模拟）（1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD．求证：EF＝BE+FD；
（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？
（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．
【变式2-2】（2021春•北碚区校级期末）如图，已知凸五边形ABCDE中，EC，EB为其对角线，EA＝ED．
（1）如图1，若∠A＝60°，∠CDE＝120°，且CD+AB＝BC．求证：EC平分∠BCD；
（2）如图2，∠A与∠D互补，∠DEA＝2∠CEB，若凸五边形ABCDE面积为30，且CD＝AB＝4．求点E到BC的距离．
1．已知，如图，AD∥BC，AE平分∠BAD，BE平分∠ABC，求证：AD+BC＝AB．
2.（2020秋•綦江区期末）如图，在△ABC中，∠A＝60°，∠ABC、∠ACB的平分线分别交AC、AB于点D、E，CE、BD相交于点F，连接DE．
（1）若AC＝BC＝7，求DE的长；
（2）求证：BE+CD＝BC．
3.（2020秋•建华区期末）阅读下面文字并填空：
数学习题课上李老师出了这样一道题：“如图1，在△ABC中，AD平分∠BAC，∠B＝2∠C．求证：AB+BD＝AC．”
李老师给出了如下简要分析：要证AB+BD＝AC，就是要证线段的和差问题，所以有两个方法：
方法一：“截长法”．如图2，在AC上截取AE＝AB，连接DE，只要证BD＝ 即可，这就将证明线段和差问题 为证明线段相等问题，只要证出△ ≌△ ，得出∠B＝∠AED及BD＝ ，再证出∠ ＝ ，进而得出ED＝EC，则结论成立．此种证法的基础是“已知AD平分∠BAC，将△ABD沿直线AD对折，使点B落在AC边上的点E处”成为可能．
方法二：“补短法”．如图3，延长AB至点F，使BF＝BD．只要证AF＝AC即可，此时先证∠ ＝∠C，再证出△ ≌△ ，则结论成立．
“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法．
4．（2019秋•四川期中）我们知道，利用三角形全等可以证明两条线段相等．但是我们会碰到这样的“和差”问题：“如图①，AD为△ABC的高，∠ABC＝2∠C，证明：CD＝AB+BD”．我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题：在CD上截取DE＝BD，连接AE．
（1）请补写完这个证明：
（2）运用上述方法证明：如图②，AD平分∠BAC，∠ABC＝2∠C，证明：BD＝AC﹣AB．
5．（2020春•南岸区期末）在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C．且BD＝CD，点E，F分别在边AM和AN上．
（1）如图1，若∠BED＝∠CFD，请说明DE＝DF；
（2）如图2，若∠BDC＝120°，∠EDF＝60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由．