人教版数学八上高分突破训练专项13 与尺规作图有关的计算和证明的综合应用（2份，原卷版+解析版）

这是一份人教版数学八上高分突破训练专项13 与尺规作图有关的计算和证明的综合应用（2份，原卷版+解析版），文件包含人教版数学八上高分突破训练专项13与尺规作图有关的计算和证明的综合应用原卷版doc、人教版数学八上高分突破训练专项13与尺规作图有关的计算和证明的综合应用解析卷doc等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
1. 分别以点 A、B 为圆心，以大于 AB 的长为半径作弧，两弧相交于 C、D 两点；
2. 作直线 CD，CD 为所求直线
垂直平分线的性质：
垂直平分线上的点到两边的距离相等
【典例1】（2021秋•邓州市期末）在△AMN中，∠MAN＞90°，AM的垂直平分线交MN于B，交AM于E，AN的垂直平分线交MN于C，交AN于F．
（1）若AM＝AN，∠MAN＝120°，则△ABC的形状是 ；
（2）去掉（1）中的“∠MAN＝120°”的条件，其他不变，判断△ABC的形状，并证明你的结论；
（3）当∠M与∠N满足怎样的数量关系时，△ABC是等腰三角形？直接写出所有可能的情况．
【解答】解：（1）等边三角形，
理由：∵AM＝AN，∠MAN＝120°，
∴∠M＝∠N＝30°，
∵BE是线段AM的垂直平分线，
∴AB＝BM，
∴∠MAB＝∠M＝30°，
∴∠ABC＝∠M+∠MAB＝60°，
同理，CA＝NC，
∴∠NAC＝∠N＝30°，
∴∠ACM＝∠N+∠NAC＝60°，
∴△ABC为等边三角形，
故答案为：等边三角形；
（2）△ABC是等腰三角形，
理由：∵AM＝AN，
∴∠M＝∠N，
∵∠MAB＝∠M，∠ABC＝∠M+∠MAB，∠NAC＝∠N，∠ACB＝∠N+∠NAC，
∴∠ABC＝∠ACB，
∴AB＝AC，
∴△ABC是等腰三角形；
（3）当∠M＝∠N时，AB＝AC；
当2∠M+∠N＝90°时，∠BAN＝90°，
∴CF∥BN，
∵CF垂直平分AN，
∴AF＝FN，
∴CN＝BC，
∴CA＝NB＝BC，
同理，当∠M+2∠N＝90°时，BA＝BC，
综上所述，当∠M＝∠N、2∠M+∠N＝90°、∠M+2∠N＝90°时，△ABC是等腰三角形．
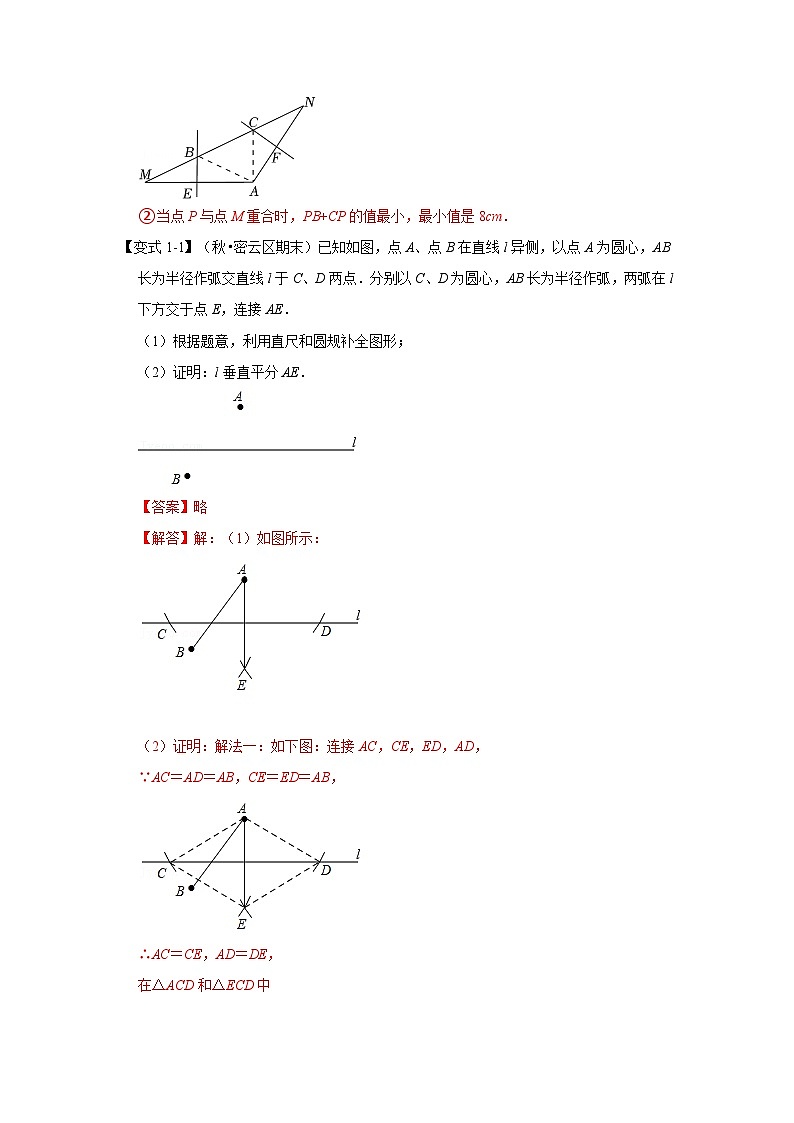
②当点P与点M重合时，PB+CP的值最小，最小值是8cm．
【变式1-1】（秋•密云区期末）已知如图，点A、点B在直线l异侧，以点A为圆心，AB长为半径作弧交直线l于C、D两点．分别以C、D为圆心，AB长为半径作弧，两弧在l下方交于点E，连接AE．
（1）根据题意，利用直尺和圆规补全图形；
（2）证明：l垂直平分AE．
【答案】略
【解答】解：（1）如图所示：
（2）证明：解法一：如下图：连接AC，CE，ED，AD，
∵AC＝AD＝AB，CE＝ED＝AB，
∴AC＝CE，AD＝DE，
在△ACD和△ECD中
∵，
∴△ACD≌△ECD（SSS），
∴∠ACD＝∠ECD，
∵AC＝CE，
∴l垂直平分AE．
解法二：如下图：连接AC，CE，ED，AD，
∵AC＝AD＝AB，CE＝ED＝AB，
∴AC＝CE，AD＝DE，
∴l垂直平分AE．
【变式1-2】（2020•建湖县模拟）如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若∠A＝25°，则∠CDB＝（ ）
A．25°B．50°C．60°D．90°
【答案】B
【解答】解：∵根据做法可知：MN是AB的垂直平分线，
∴AD＝BD，
∵△ADC的周长为10，
∴AD+CD+AC＝10，
∴BD+DC+AC＝10，
∴AC+BC＝10，
∵AB＝7，
∴△ABC的周长为AB+AC+BC＝7+10＝17，
故选：B．
【变式1-3】（2021春•龙泉驿区期末）如图，在△ABC中，线段AB的垂直平分线与AC相交于点D，连接BD，边AC的长为12cm，边BC的长为7cm，则△BCD的周长为（ ）
A．18cmB．19cmC．20cmD．21cm
【答案】B
【解答】解：∵线段AB的垂直平分线与AC相交于点D，
∴DA＝DB，
∴△BCD的周长＝BC+CD+DB＝BC+CD+DA＝BC+AC，
∵AC＝12cm，BC＝7cm，
∴△BCD的周长＝BC+AC＝12+7＝19（cm），
故选：B．
【变式1-4】（2022春•郓城县期末）如图，在△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，交AB于点E．
（1）求证：△ABD是等腰三角形；
（2）若∠A＝40°，求∠DBC的度数；
（3）若AE＝6，△CBD的周长为20，求△ABC的周长．
【解答】解：（1）证明：∵AB的垂直平分线MN交AC于点D，
∴DB＝DA，
∴△ABD是等腰三角形；
（2）∵△ABD是等腰三角形，∠A＝40°，
∴∠ABD＝∠A＝40°，∠ABC＝∠C＝（180°﹣40°）÷2＝70°
∴∠DBC＝∠ABC﹣∠ABD＝70°﹣40°＝30°；
（3）∵AB的垂直平分线MN交AC于点D，AE＝6，
∴AB＝2AE＝12，
∵△CBD的周长为20，
∴AC+BC＝20，
∴△ABC的周长＝AB+AC+BC＝12+20＝32．
【变式1-5】（2021秋•思南县校级月考）如图，在△ABC中，AC边的垂直平分线DM交AC于D，CB边的垂直平分线EN交BC于E，DM与EN相交于点F．
（1）若△CMN的周长为16cm，求AB的长；
（2）若∠MFN＝70°，求∠MCN的度数．
【解答】解：（1）∵DM是AC边的垂直平分线，
∴MA＝MC，
同理，NC＝NB，
∵△CMN的周长为16cm，
∴MC+MN+NC＝16cm，
∴AB＝AM+MN＝BN＝16cm；
（2）∵AC边的垂直平分线DM交AC于D，CB边的垂直平分线EN交BC于E，
∴MD⊥AC，NE⊥BC，
∴∠ACB＝180°﹣∠MFN＝110°，
∴∠A+∠B＝70°，
∵MA＝MC，NB＝NC，
∴∠MCA＝∠A，∠NCB＝∠B，
∴∠MCN＝∠ACB﹣（∠MCA+∠NCB）＝∠ACB﹣（∠A+∠B）＝110°﹣70°＝40°．
1.（2021春•和平区校级期中）如图，在△ABC中，∠A＝45°，∠B＝30°．用直尺和圆规在边AB上确定一点D．则∠ACD的大小为（ ）
A．60°B．75°C．65°D．70°
【答案】B
【解答】解：由尺规作图可知，线段BC的垂直平分线交AB于D，
∴DC＝DB，
∴∠DCB＝∠B＝30°，
∵∠A＝45°，∠B＝30°，
∴∠ACB＝180°﹣∠A﹣∠B＝105°，
∴∠ACD＝∠ACB﹣∠DCB＝75°，
故选：B
2．（2020•宝安区二模）如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于M、N两点，连接MN，交AB于点H，以点H为圆心，HA的长为半径作的弧恰好经过点C，以点B为圆心，BC的长为半径作弧交AB于点D，连接CD，若∠A＝22°，则∠BDC＝（ ）
A．52°B．55°C．56°D．60°
【答案】C
【解答】解：连接CH，
由题意得，直线MN是线段AB的垂直平分线，
∴AH＝BH，
∵CH＝AH，
∴CH＝AB，
∴∠ACB＝90°，
∵∠A＝22°，
∴∠ACH＝∠A＝22°，
∴∠BCH＝∠B＝68°，
∵BC＝BD，
∴∠BDC＝∠BCD＝（180°﹣68°）＝56°，
故选：C．
3．（2021•长春一模）如图，∠AOB＝30°．按下列步骤作图：①在射线OA上取一点C，以点O为圆心，OC长为半径作圆弧DE，交射线OB于点F，连接CF；②以点F为圆心，CF长为半径作圆弧，交弧DE于点G；③连接FG、CG，作射线OG．根据以上作图过程及所作图形，下列结论中错误的是（ ）
A．∠AOG＝60°B．OF垂直平分CG
C．OG＝CGD．OC＝2FG
【答案】D
【解答】解：由作法得OC＝OF＝OG，FG＝FC，
则OF垂直平分CG，所以B选项的结论正确；
∵C点与G点关于OF对称，
∴∠FOG＝∠FOC＝30°，
∴∠AOG＝60°，所以A选项的结论正确；
∴△OCG为等边三角形，
∴OG＝CG，所以C选项的结论正确；
在Rt△OCM中，∵∠COM＝30°，
∴OC＝2CM，
∵CF＞CM，FC＝FG，
∴OC≠2FG，所以D选项的结论错误．
故选：D．
4．（2020秋•鄞州区期末）如图，△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，若∠BAC＝100°，则∠EAG的度数是（ ）
A．10°B．20°C．30°D．40°
【答案】B
【解答】解：∵∠BAC＝100°，
∴∠C+∠B＝180°﹣100°＝80°，
∵DE是AB的垂直平分线，
∴EA＝EB，
∴∠EAB＝∠B，
同理∠GAC＝∠C，
∴∠EAB+∠GAC＝∠C+∠B＝80°，
∴∠EAG＝100°﹣80°＝20°，
故选：B．
5．（2021春•叶县期末）如图，在△ABC中，∠B＝30°，∠C＝40°．
（1）尺规作图：①作边AB的垂直平分线交BC于点D；
②连接AD，作∠CAD的平分线交BC于点E；（要求：保留作图痕迹，不写作法）
（2）在（1）所作的图中，求∠DAE的度数．
【答案】略
【解答】解：（1）如图，点D，射线AE即为所求．
（2）∵DF垂直平分线段AB，
∴DB＝DA，
∴∠DAB＝∠B＝30°，
∵∠C＝40°，
∴∠BAC＝180°﹣30°﹣40°＝110°，
∴∠CAD＝110°﹣30°＝80°，
∵AE平分∠DAC，
∴∠DAE＝∠DAC＝40°．
6．（2021秋•洪江市期末）如图，直线l与m分别是△ABC边AC和BC的垂直平分线，l与m分别交边AB于点D和点E．
（1）若AB＝10，则△CDE的周长是多少？为什么？
（2）若∠ACB＝125°，求∠DCE的度数．
【解答】解：（1）△CDE的周长为10．
∵直线l与m分别是△ABC边AC和BC的垂直平分线，
∴AD＝CD，BE＝CE，
∴△CDE的周长＝CD+DE+CE＝AD+DE+BE＝AB＝10；
（2）∵直线l与m分别是△ABC边AC和BC的垂直平分线，
∴AD＝CD，BE＝CE，
∴∠A＝∠ACD，∠B＝∠BCE，
又∵∠ACB＝125°，
∴∠A+∠B＝180°﹣125°＝55°，
∴∠ACD+∠BCE＝55°，
∴∠DCE＝∠ACB﹣（∠ACD+∠BCE）＝125°﹣55°＝70°．
7．（2021秋•兴山县期末）如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于N，交AC于M．
（1）若∠B＝70°，则∠NMA的度数是 ；
（2）探究∠B与∠NMA的关系，并说明理由；
（3）连接MB，若AB＝8cm，△MBC的周长是14cm．
①求BC的长；
②在直线MN上是否存在点P，使PB+CP的值最小？若存在，标出点P的位置并求PB+CP的最小值；若不存在，说明理由．
【解答】解：（1）若∠B＝70°，则∠NMA的度数是 50°，
故答案为：50°；
（2）猜想的结论为：∠NMA＝2∠B﹣90°．
理由：∵AB＝AC，
∴∠B＝∠C，
∴∠A＝180°﹣2∠B，
又∵MN垂直平分AB，
∴∠NMA＝90°﹣∠A＝90°﹣（180°﹣2∠B）＝2∠B﹣90°．
（3）如图：
①∵MN垂直平分AB．
∴MB＝MA，
又∵△MBC的周长是14cm，
∴AC+BC＝14cm，
∴BC＝6cm．