人教版数学八上高分突破训练专项15 等边三角形常考作辅助线法（2份，原卷版+解析版）

这是一份人教版数学八上高分突破训练专项15 等边三角形常考作辅助线法（2份，原卷版+解析版），文件包含人教版数学八上高分突破训练专项15等边三角形常考作辅助线法原卷版doc、人教版数学八上高分突破训练专项15等边三角形常考作辅助线法解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
技巧1：作平行线法
技巧2：截长补短法
【典例1】（烟台）如图，在等边三角形ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．
【问题解决】
如图1，若点D在边BC上，求证：CE+CF＝CD；
【类比探究】
如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
【变式1-1】（2020秋•句容市期中）如图，在等边三角形ABC中，点E是边AC上一定点，点D是射线BC上一动点，以DE为一边作等边三角形DEF，连接CF．
【问题解决】如图1，点D与点B重合，求证：AE＝FC；
【类比探究】（1）如图2，点D在边BC上，求证：CE+CF＝CD；
（2）如图3，点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？直接写出你的结论．
【变式1-2】（天心区期中）如图，在等边△ABC中，点D是边AC上一定点，点E是直线BC上一动点，以DE为一边作等边△DEF，连接CF．
（1）如图1，若点E在边BC上，且DE⊥BC，垂足为E，求证：CD＝2CE；
（2）如图1，若点E在边BC上，且DE⊥BC，垂足为E，求证：CE+CF＝CD；
（3）如图2，若点E在射线CB上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
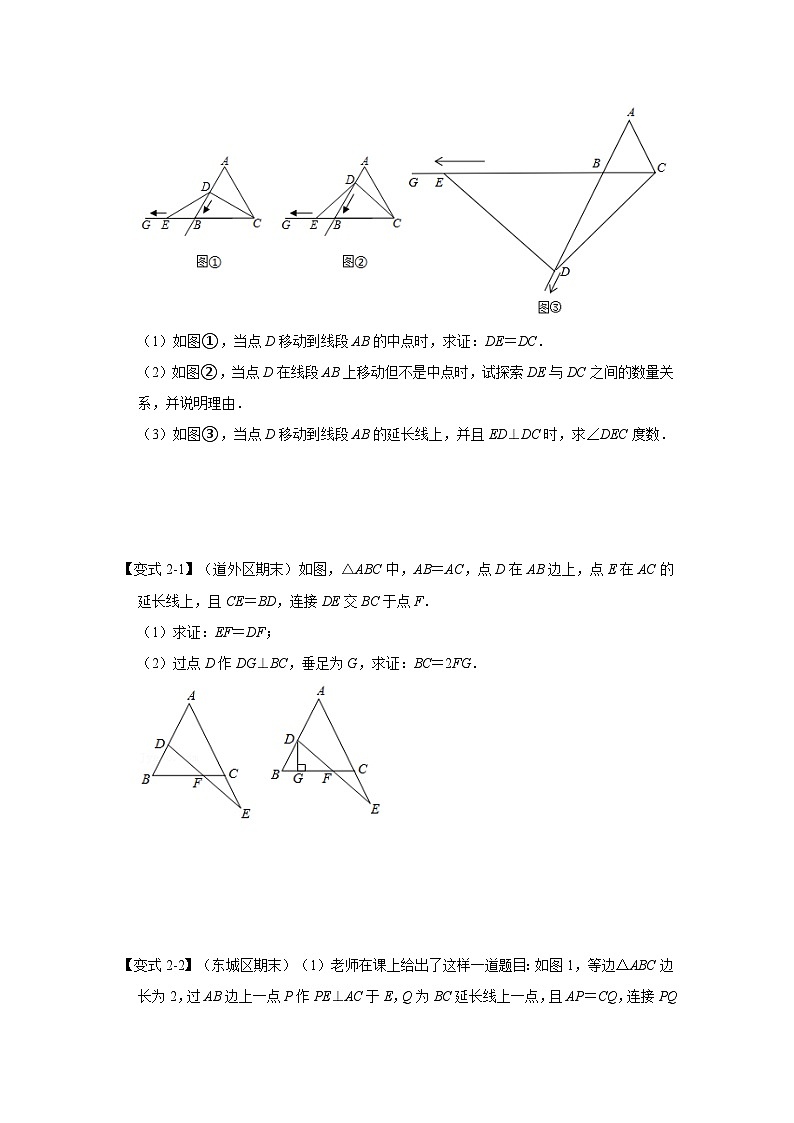
【典例2】（2020秋•湖南期末）如图，△ABC是等边三角形，点D、E分别是射线AB、射线CB上的动点，点D从点A出发沿射线AB移动，点E从点B出发沿BG移动，点D、点E同时出发并且运动速度相同．连接CD、DE．
（1）如图①，当点D移动到线段AB的中点时，求证：DE＝DC．
（2）如图②，当点D在线段AB上移动但不是中点时，试探索DE与DC之间的数量关系，并说明理由．
（3）如图③，当点D移动到线段AB的延长线上，并且ED⊥DC时，求∠DEC度数．
【变式2-1】（道外区期末）如图，△ABC中，AB＝AC，点D在AB边上，点E在AC的延长线上，且CE＝BD，连接DE交BC于点F．
（1）求证：EF＝DF；
（2）过点D作DG⊥BC，垂足为G，求证：BC＝2FG．
【变式2-2】（东城区期末）（1）老师在课上给出了这样一道题目：如图1，等边△ABC边长为2，过AB边上一点P作PE⊥AC于E，Q为BC延长线上一点，且AP＝CQ，连接PQ交AC于D，求DE的长．
小明同学经过认真思考后认为，可以通过过点P作平行线构造等边三角形的方法来解决这个问题．
请根据小明同学的思路直接写出DE的长．
（2）【类比探究】
老师引导同学继续研究：
1．等边△ABC边长为2，当P为BA的延长线上一点时，作PE⊥CA的延长线于点E，Q为边BC上一点，且AP＝CQ，连接PQ交AC于D．请你在图2中补全图形并求DE的长．
2．已知等边△ABC，当P为AB的延长线上一点时，作PE⊥射线AC于点E，Q为 ② （①BC边上；②BC的延长线上；③CB的延长线上）一点，且AP＝CQ，连接PQ交直线AC于点D，能使得DE的长度保持不变．（将答案的编号填在横线上）
1．（2021秋•咸丰县期末）如图，等边△ABC的边长为12cm，D为AC边上一动点，E为AB延长线上一动点，DE交CB于点P，点P为DE中点
（1）求证：CD＝BE；
（2）若DE⊥AC，求BP的长．
2．（2021秋•绵竹市期末）在等边△ABC中，点E是AB上的动点，点E与点A、B不重合，点D在CB的延长线上，且EC＝ED．
（1）如图1，若点E是AB的中点，求证：BD＝AE；
（2）如图2，若点E不是AB的中点时，（1）中的结论“BD＝AE”能否成立？若不成立，请直接写出BD与AE数量关系，若成立，请给予证明．
3.（2020秋•旅顺口区期中）如图，在等边三角形ABC中，点E是边CA延长线上一点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．
（1）如图1，若点D在边BC上，求证：CE＝CF+CD；
（2）如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系，并说明理由．
4.（2020•安徽）如图，D是等边△ABC的边AB上一点，E是BC延长线上一点，CE＝DA，连接DE交AC于F，过D点作DG⊥AC于G点．证明下列结论：
（1）AG＝AD；
（2）DF＝EF；
（3）S△DGF＝S△ADG+S△ECF．
5．（2020秋•花雨区校级月考）我们在前面曾遇到过这样一道题目：
小明与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE DB（填“＞”、“＜”或“＝”）
（2）一般情况，证明结论：如图2，过点E作EF∥BC，交AC于点F． 请你继续完成对以上问题（1）中所填写结论的证明．
（3）变式探究：如图3，△ABC是等边三角形，D是边BC上一点，点E在BA的延长线上，且BD＝AE，此时，CE和DE有何数量关系？请画出图形，作出判断，并说明理
6．（2020秋•河西区期末）如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（1）当∠BQD＝30°时，求AP的长；
（2）证明：在运动过程中，点D是线段PQ的中点；
（3）当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．
7．（2020秋•裕华区校级期末）知识链接：将两个含30°角的全等三角尺放在一起，让两个30°角合在一起成60°，经过拼凑、观察、思考，探究出结论“直角三角形中，30°角所对的直角边等于斜边的一半”．
如图，等边三角形ABC的边长为4cm，点D从点C出发沿CA向A运动，点E从B出发沿AB的延长线BF向右运动，已知点D、E都以每秒0.5cm的速度同时开始运动，运动过程中DE与BC相交于点P，设运动时间为x秒．
（1）请直接写出AD长．（用x的代数式表示）
（2）当△ADE为直角三角形时，运动时间为几秒？
（3）求证：在运动过程中，点P始终为线段DE的中点．
8．（2021秋•营口期末）已知A（﹣10，0），以OA为边在第二象限作等边△AOB．
（1）求点B的横坐标；
（2）如下图，点M、N分别为OA、OB边上的动点，以MN为边在x轴上方作等边△MNE，连结OE，当∠EMO＝45°时，求∠MEO的度数．