人教版数学八上高分突破训练专项19 完全平方公式的几何背景（两大类型）（2份，原卷版+解析版）

这是一份人教版数学八上高分突破训练专项19 完全平方公式的几何背景（两大类型）（2份，原卷版+解析版），文件包含人教版数学八上高分突破训练专项19完全平方公式的几何背景两大类型原卷版doc、人教版数学八上高分突破训练专项19完全平方公式的几何背景两大类型解析版doc等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
【典例1】（2022秋•南昌县期中）如图1所示是一个长为2m，宽为2n的长方形，沿虚线用剪刀均分成四个小长方形，然后按图2的方式拼成一个正方形．
（1）图2中的阴影部分的正方形的边长等于 ；
（2）请用两种不同的方法列代数式表示图2中阴影部分的面积：方法① ；方法② ；
（3）观察图2，直接写出（m+n）2，（m﹣n）2，mn这三个代数式之间的等量关系；
（4）根据（3）题中的等量关系，解决如下问题：若a+b＝8，ab＝5，求（a﹣b）2的值．
【解答】解：（1）由拼图可知，图②中阴影部分的边长为m﹣n，
故答案为：m﹣n；
（2）阴影部分是边长为m﹣n的正方形，因此面积为（m﹣n）2，
阴影部分的面积可以看作从边长为m+n的正方形面积中减去4个长为m，宽n的长方形面积，即（m+n）2﹣4mn，
故答案为：（m﹣n）2，（m+n）2﹣4mn；
（3）由（2）中两种方法所表示的图形的面积相等，可得，
（m﹣n）2＝（m+n）2﹣4mn；
（4）∵a+b＝8，ab＝5，
∴（a﹣b）2＝（a+b）2﹣4ab
＝64﹣20
＝44
【变式1-1】（2022春•玄武区校级期中）观察图形，用两种不同的方法计算大长方形面积，我们可以验证等式（ ）
A．（a+b）（a+2b）＝a2+3ab+2b2
B．（a+b）（2a+b）＝2a2+3ab+b2
C．（a+b）（a+2b）＝2a2+3ab+b2
D．（a+b）（2a+b）＝a2+3ab+2b2
【答案】A
【解答】解：整体是长为a+2b，宽为a+b的长方形，因此面积为（a+2b）（a+b），
整体是由6个部分的面积和，即a2+3ab+2b2，
因此有（a+2b）（a+b）＝a2+3ab+2b2，
故选：A．
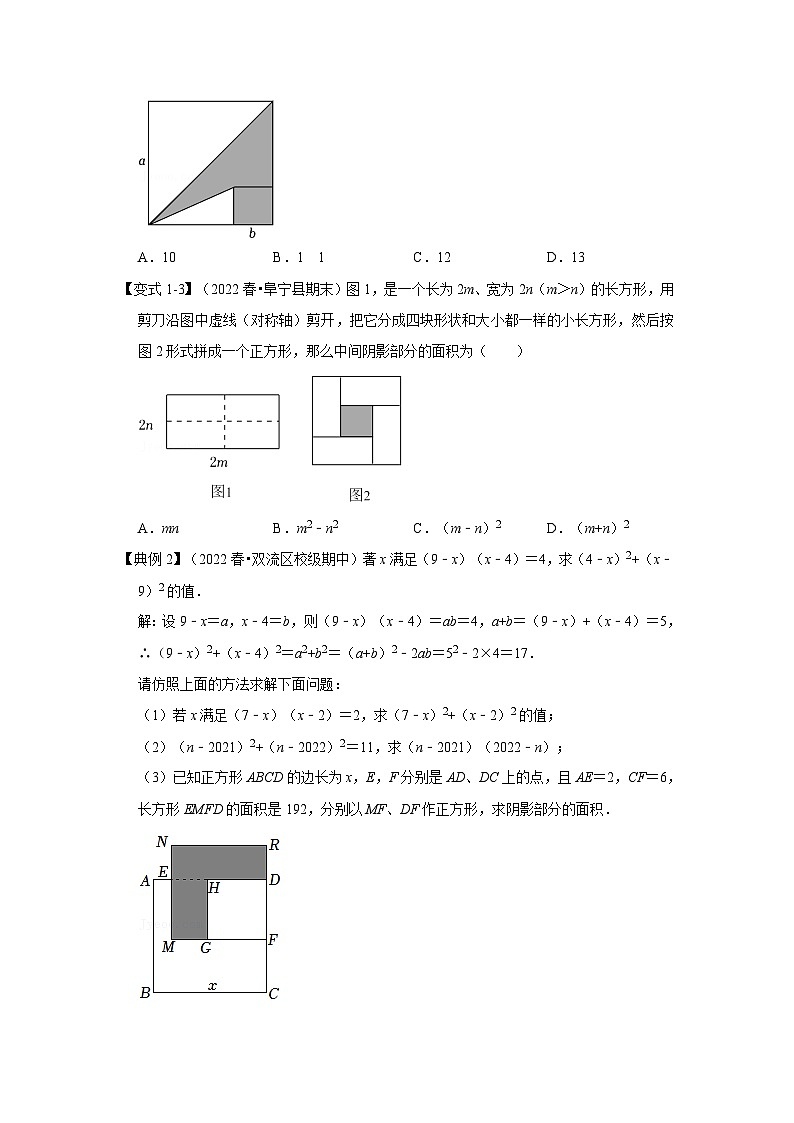
【变式1-2】（2022秋•渝中区校级月考）如图，两个正方形边长分别为a，b，已知a+b＝7，ab＝9，则阴影部分的面积为（ ）
A．10B．1 1C．12D．13
【答案】B
【解答】解：根据题意可得，
S阴＝a²﹣﹣
＝（a²﹣ab+b²）
＝[（a+b）²﹣3ab]，
把a+b＝7，ab＝9代入上式，
则S阴＝×（72﹣3×9）＝11．
故选：B．
【变式1-3】（2022春•阜宁县期末）图1，是一个长为2m、宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2形式拼成一个正方形，那么中间阴影部分的面积为（ ）
A．mnB．m2﹣n2C．（m﹣n）2D．（m+n）2
【答案】C
【解答】解：方法一：
图2中四个长方形的面积的和＝图1的长方形的面积＝2m×2n＝4mn，
图2的大正方形的面积＝（m+n）2，
图2中阴影部分的面积＝图2的大正方形的面积﹣图2中四个长方形的面积的和
＝（m+n）2﹣4mn
＝m2+2mn+n2﹣4mn
＝m2﹣2mn+n2
＝（m﹣n）2．
方法二：
图中阴影部分是正方形，且四个边长都是（m﹣n），
∴阴影部分的面积＝（m﹣n）2．
故选：C．
【典例2】（2022春•双流区校级期中）著x满足（9﹣x）（x﹣4）＝4，求（4﹣x）2+（x﹣9）2的值．
解：设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4，a+b＝（9﹣x）+（x﹣4）＝5，
∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17．
请仿照上面的方法求解下面问题：
（1）若x满足（7﹣x）（x﹣2）＝2，求（7﹣x）2+（x﹣2）2的值；
（2）（n﹣2021）2+（n﹣2022）2＝11，求（n﹣2021）（2022﹣n）；
（3）已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE＝2，CF＝6，长方形EMFD的面积是192，分别以MF、DF作正方形，求阴影部分的面积．
【解答】解：（1）设7﹣x＝a，x﹣4＝b，
则（7﹣x）（x﹣2）＝ab＝2，a+b＝7﹣x+x﹣4＝3，
∴（7﹣x）2+（x﹣2）2＝a2+b2＝（a+b）2﹣2ab＝32﹣2×2＝5；
（2）设n﹣2021＝a，n﹣2022＝b，
则（n﹣2021）2+（n﹣2022）2＝a2+b2＝11，a﹣b＝（n﹣2021）﹣（n﹣2022）＝1，
（n﹣2021）（2022﹣n）＝﹣（n﹣2021）（n﹣2022）
＝﹣ab
＝（a﹣b）2﹣（a2+b2）]
＝
＝﹣5；
（3）根据题意可得，
MF＝x﹣2，FD＝x﹣6，（x﹣2）（x﹣6）＝192，
设x﹣2＝a，x﹣6＝b，
则（x﹣2）（x﹣6）＝ab＝192，
a﹣b＝（x﹣2）﹣（x﹣6）＝4，
S阴＝（x﹣2）2﹣（x﹣6）2
＝a2﹣b2
＝（a+b）（a﹣b）
＝（a﹣b）
＝×4
＝28×4
＝112．
阴影部分的面积为112．
【变式2】（2022春•盐都区月考）阅读理解：若x满足（30﹣x）（x﹣10）＝160，求（30﹣x）2+（x﹣10）2的值．
解：设30﹣x＝a，x﹣10＝b，则（30﹣x）（x﹣10）＝ab＝160，a+b＝（30﹣x）+（x﹣10）＝20，（30﹣x）2+（x﹣10）2＝a2+b2＝（a+b）2﹣2ab＝202﹣2×160＝80
解决问题：
（1）若x满足（2020﹣x）（x﹣2016）＝2，则（2020﹣x）2+（x﹣2016）2＝ ；
（2）若x满足（x﹣2022）2+（x﹣2018）2＝202，求（x﹣2022）（x﹣2018）的值；
（3）如图，在长方形ABCD中，AB＝16，BC＝12，点E．F是BC、CD上的点，且BE＝DF＝x，分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN，若长方形CEPF的面积为100平方单位，则图中阴影部分的面积和为 平方单位．
【解答】解：（1）设2020﹣x＝a，x﹣2016＝b，
则（2020﹣x）（x﹣2016）＝ab＝2，a+b＝（2020﹣x）+（x﹣2016）＝4，
（2020﹣x）2+（x﹣2016）2＝a2+b2＝（a+b）2﹣2ab＝42﹣2×2＝12；
故答案为：12；
（2）设x﹣2022＝a，x﹣2018＝b，
则（x﹣2022）2+（x﹣2018）2＝a2+b2＝202，a﹣b＝（x﹣2022）﹣（x﹣2018）＝﹣4，
（x﹣2022）（x﹣2018）
＝ab
＝﹣[（a﹣b）2﹣（a2+b2）]
＝[（﹣4）2﹣202]
＝93；
（3）根据题意可得，
CF＝CD﹣DF＝16﹣x，CE＝BC﹣BE＝12﹣x，
（16﹣x）（12﹣x）＝100，
设16﹣x＝a，12﹣x＝b，则（16﹣x）（12﹣x）＝ab＝100，
a﹣b＝（16﹣x）﹣（12﹣x）＝4，
S阴＝（16﹣x）2+（12﹣x）2
＝a2+b2
＝（a﹣b）2+2ab
＝42+2×100
＝216．
图中阴影部分的面积和为216平方单位．
故答案为：216．
1．（2022春•盱眙县期中）如图，点C是线段BG上的一点，以BC，CG为边向两边作正方形，面积分别是S1和S2，两正方形的面积和S1+S2＝20，已知BG＝6，则图中阴影部分面积为（ ）
A．4B．6C．7D．8
【答案】A
【解答】解：设BC＝a，CG＝b，
∵四边形CEFG是正方形，
∴CE＝CG＝b，
∵两正方形的面积和S1+S2＝20，
∴a2+b2＝20，
∵a+b＝6，
∴（a+b）2＝a2+b2+2ab＝36，
∴ab＝8，
∴S阴＝ab＝4，
故选：A．
2．（2022春•庐阳区校级期中）如图所示，以长方形ABCD的各边为直径向外作半圆得到一个新的图形其周长为16π，同时此图形中四个半圆面积之和为44π，则长方形ABCD的面积为（ ）
A．10B．20C．40D．80
【答案】C
【解答】解：设AB＝a，BC＝b，
由题意得：πa+πb＝16π，π×+π×＝44π．
∴a+b＝16，a2+b2＝176．
∵（a+b）2＝a2+b2+2ab．
∴256＝176+2ab．
∴ab＝40．
∴S长方形ABCD＝40．
故选：C．
3．（2022春•太原期中）通过两种不同的方法计算同一图形的面积可以得到一个数学等式，用这种方法可得到整式乘法中的一些运算法则或公式，例如，由图1可得等式（a+b）（c+d）＝ac+ad+bc+bd，即为多项式乘法法则．利用图2可得的乘法公式为（ ）
A．（a+b）2＝a2+b2B．（a+b）2＝a2+2ab+b2
C．（a+b）2＝a2+b2+abD．（a+b）（a+b）＝a2+b2
【答案】B
【解答】解：根据图2可得，（a+b）2＝a2+2ab+b2，
故选：B．
4．（2022春•新泰市期中）图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
（1）求图2中的阴影部分的正方形的周长；
（2）观察图2，请写出下列三个代数式（a+b）2，（a﹣b） 2，ab之间的等量关系；
（3）如图3，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝8，两正方形的面积和S1+S2＝24，运用你由（2）所得到的等量关系，求图中阴影部分面积．
【解答】解：（1）根据题意可得，
阴影部分的正方形的周长为4（a﹣b）；
（2）根据题意可得，
（a+b）²＝（a﹣b）²+4ab；
（3）设AC＝a，BC＝b，
则a+b＝8，a²+b²＝24，
根据题意可得，
S阴＝ab＝[（a+b）²﹣（a²+b²）]＝×（82﹣24）＝10．
5．（2022秋•上蔡县校级月考）（1）试用两种不同的方法表示图1中阴影部分的面积，从中你有什么发现，请用等式表示出来；
（2）利用你发现的结论，解决下列问题：
①如图2，两个正方形的边长分别为a，b，且a+b＝ab＝9，求图2中阴影部分的面积．
②已知4a2+b2＝57，ab＝6，求2a+b的值；
③若（20﹣x）（x﹣30）＝10，则（20﹣x）2+（x﹣30）2的值是 ．
【解答】解：（1）根据题意可得，
方法一：S阴＝a2+b2，
方法二：S阴＝（a+b）2﹣2ab＝a2+b2；
（2）①根据题意可得，
S阴＝a2+b2﹣（a+b）b﹣a2
＝（a2﹣ab+b2），
∵a+b＝ab＝9，
∴a2+b2＝（a+b）2﹣2ab＝92﹣2×9＝63，
∴S阴＝×（63﹣9）＝27；
②（2a+b）2＝4a2+b2+4ab＝57+4×6＝81，
∴2a+b＝±9；
③设20﹣x＝a，x﹣30＝b，
则（20﹣x）（x﹣30）＝ab＝10，a+b＝（20﹣x）+（x﹣30）＝﹣10；
∴（20﹣x）2+（x﹣30）2＝a2+b2＝（a+b）2﹣2ab＝（﹣10）2﹣2×10＝80．
故答案为：80．
6．（2022春•顺德区校级期中）如图所示，在边长为a米的正方形草坪上修建两条宽为b米的道路．
（1）为了求得剩余草坪的面积，小明同学想出了两种办法，结果分别如下：方法①： .方法②： .请你从小明的两种求面积的方法中，直接写出含有字母a，b代数式的等式是： ．
（2）根据（1）中的等式，解决如下问题：①已知：a﹣b＝5，a2+b2＝20，求ab的值；②已知：（x﹣2020）2+（x﹣2022）2＝12，求（x﹣2021）2的值．
【解答】解：（1）方法①，通过平移两条路，草坪可看作边长为（a﹣b）米的正方形，因此面积为（a﹣b）2（平方米），方法②，从大正方形面积里减去两条路的面积，即（a2﹣ab﹣ab+b2）平方米，也就是（a2﹣2ab+b2）平方米，所以有（a﹣b）2＝a2﹣2ab+b2，
故答案为：（a﹣b）2，a2﹣2ab+b2，（a﹣b）2＝a2﹣2ab+b2；
（2）①∵a﹣b＝5，
∴a2﹣2ab+b2＝25，
又∵a2+b2＝20，
∴ab＝﹣；
②设x﹣2020＝m，x﹣2022＝n，则m﹣n＝2，m2+n2＝（x﹣2020）2+（x﹣2022）2＝12，
∴m2﹣2mn+n2＝4，即12﹣2mn＝4，
∴mn＝4，
∴（m+n）2＝（m﹣n）2+4mn
＝4+16
＝20，
∴（x﹣2021）2
＝（）2
＝
＝
＝5，
答：（x﹣2021）2的值为5．
7．（2022春•上虞区期末）图1是一个长为2b，宽为2a的长方形，沿虚线平均分成四块，然后按图2拼成一个正方形．解答下列问题．
（1）图2中阴影部分的面积可表示为 ；对于（b﹣a）2，（b+a）2，ab，这三者间的等量关系为 ．
（2）利用（1）中所得到的结论计算：若x+y＝﹣3，xy＝﹣，则x﹣y＝ ．
（3）观察图3，从图中你能得到怎样的一个代数恒等式？再根据你所得到的这个代数恒等式探究：若m2+4mn+3n2＝0（n≠0），试求的值．
【解答】解：（1）阴影部分是边长为b﹣a的正方形，因此面积为（b﹣a）2，
根据拼图以及面积之间的关系可得，（b﹣a）2，（b+a）2，ab，这三者间的等量关系为（b﹣a）2＝（b+a）2﹣4ab，
故答案为：（b﹣a）2；（b﹣a）2＝（b+a）2﹣4ab；
（2）由（1）可得，
（x﹣y）2＝（x+y）2﹣4xy＝9+7＝16，
∴x﹣y＝±4，
故答案为：±4；
（3）整个长方形是长为a+3b，宽为a+b，因此面积为（a+3b）（a+b），整个长方形的面积也可看作8个部分的面积和，即a2+4ab+3b2，
因此有（a+3b）（a+b）＝a2+4ab+3b2；
∵m2+4mn+3n2＝0（n≠0），即（m+n）（m+3n）＝0，
∴m+n＝0或m+3n＝0，
∴＝﹣1或＝﹣3．
8．（2022春•包头期末）如图，学校有一块长为（a+2b）m，宽为（a+b）m的长方形土地，四个角留出四个边长为（b﹣a）m的小正方形空地，剩余部分进行绿化．
（1）用含a、b的式子表示要进行绿化的土地面积；（结果要化简）
（2）当a＝6，b＝10时，求要进行绿化的土地面积．
【解答】解：（1）由于S绿化面积＝S长方形﹣4S小正方形，因此有，
（a+b）（a+2b）﹣4（b﹣a）2
＝a2+3ab+2b2﹣4a2+8ab﹣4b2
＝（11ab﹣3a2﹣2b2）m2，
答：绿化的面积为（11ab﹣3a2﹣2b2）m2；
（2）当a＝6，b＝10时，
原式＝660﹣108﹣200＝352（m2）
答：当a＝6，b＝10时，绿化的土地面积为352m2．
9．（2022•平泉市一模）如图，将一张矩形大铁皮切割成九块，切痕为虚线所示，其中有两块是边长都为m厘米的大正方形，两块是边长都为n厘米的小正方形，五块是长宽分别是m厘米、n厘米的全等小矩形，且m＞n．
（1）用含m、n的代数式表示切痕总长L；
（2）若每块小矩形的面积为30平方厘米，四个正方形的面积和为180平方厘米，试求（m+n）2的值．
【解答】解：（1）L＝2（m+2n）+2（2m+n）
＝2m+4n+4m+2n
＝6m+6n（cm）；
（2）每块小矩形的面积为30cm2，即mn＝30cm2，
四个正方形的面积为180cm2，即m2+n2＝90cm2，
∴（m+n）2＝m2+2mn+n2，
＝90+2×30
＝90+60
＝150（cm2）．
10．（2022春•江都区期中）把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
例如，由图①，从整体看，是一个面积为可得等式：（a+2b）（a+b）＝a2+3ab+2b2．
（1）（i）由图②，可得等式： ；
（ii）利用（i）所得等式，若a+b+c＝11，ab+bc+ac＝38，则a2+b2+c2＝ ；
（2）如图③，将边长分别为a、b的两个正方形拼在一起，B、C、G三点在同一直线上，连接BD和BF，若这两个正方形的边长a、b满足a+b＝10，ab＝20．请求出阴影部分的面积；
（3）图④中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片，现有足量的这三种纸片．
（i）请用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形，并仿照图①②画出拼法并标注a、b；
（ii）结合（i）拼图试着分解因式2a2+5ab+2b2．
【解答】解：（1）（i）由题意得，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac，
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（ii）∵a+b+c＝11，ab+bc+ac＝38，
∴a2+b2+c2＝（a+b+c）2﹣2（ab+ac+bc）＝121﹣76＝45；
故答案为：45；
（2）∵a+b＝10，ab＝20，
∴S阴影＝a2+b2﹣（a+b）•b﹣a2＝a2+b2﹣ab＝（a+b）2﹣ab＝×102﹣×20＝50﹣30＝20；
（3）（i）根据题意，作出图形如下：
（ii）由上面图形可知，2a2+5ab+2b2＝（a+2b）（2a+b）．
11．（2022秋•高青县期中）对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到（a+b）2＝a2+2ab+b2，请解答下列问题：
（1）写出图2中所表示的数学等式；
（2）根据整式乘法的运算法则，通过计算验证上述等式；
（3）若a+b+c＝10，ab+ac+bc＝35，利用得到的结论求a2+b2+c2的值．
【解答】解：（1）图2整体是边长为a+b+c的正方形，因此面积为（a+b+c）2，图2也可以看作9个部分的面积和，即a2+b2+c2+2ab+2bc+2ac，
因此有（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（2）（a+b+c）2＝（a+b+c）（a+b+c）
＝a2+ab+ac+ab+b2+bc+ac+bc+c2
＝a2+b2+c2+2ab+2ac+2bc，
即：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，
（3）把a+b+c＝10，ab+ac+bc＝35，代入（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，得
100＝a2+b2+c2+2×35，
∴a2+b2+c2＝100﹣70＝30，
答：a2+b2+c2的值为30．