人教版数学八年级上册【阶段复习】专题01 三角形（基础精炼卷）（原卷+解析）

这是一份人教版数学八年级上册【阶段复习】专题01 三角形（基础精炼卷）（原卷+解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
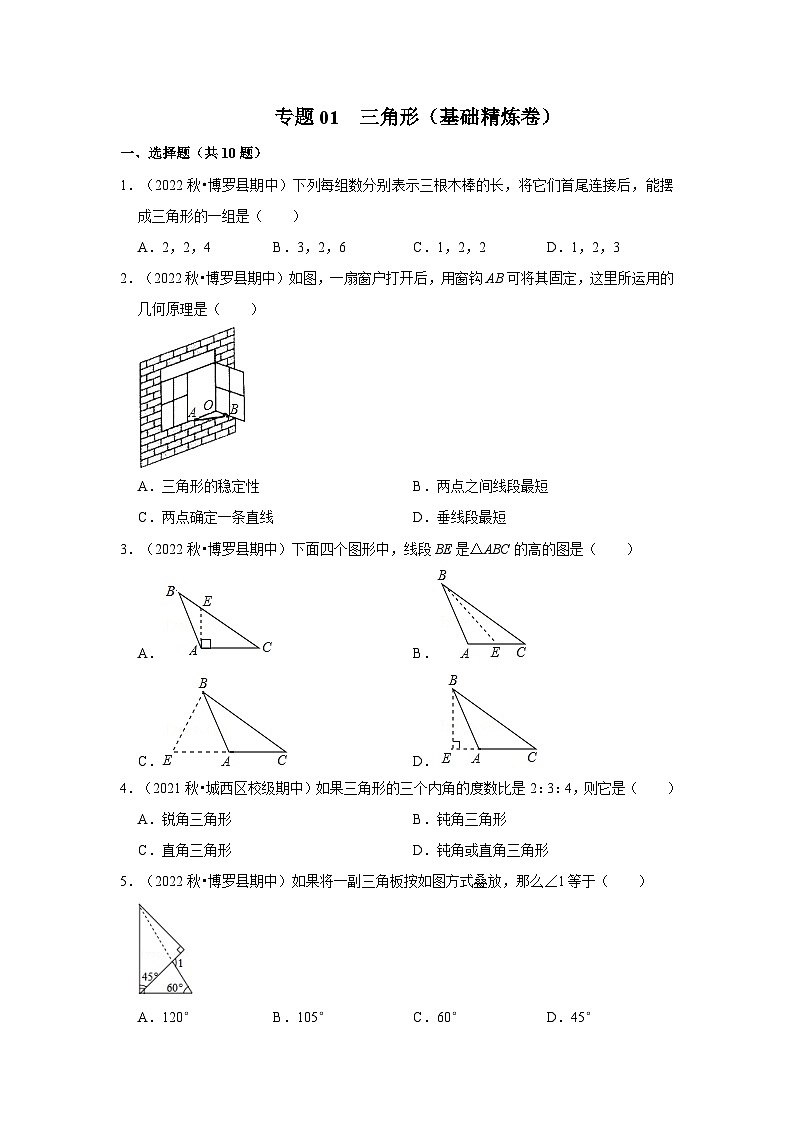
1．（2022秋•博罗县期中）下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（ ）
A．2，2，4B．3，2，6C．1，2，2D．1，2，3
2．（2022秋•博罗县期中）如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（ ）
A．三角形的稳定性B．两点之间线段最短
C．两点确定一条直线D．垂线段最短
3．（2022秋•博罗县期中）下面四个图形中，线段BE是△ABC的高的图是（ ）
A．B．
C．D．
4．（2021秋•城西区校级期中）如果三角形的三个内角的度数比是2：3：4，则它是（ ）
A．锐角三角形B．钝角三角形
C．直角三角形D．钝角或直角三角形
5．（2022秋•博罗县期中）如果将一副三角板按如图方式叠放，那么∠1等于（ ）
A．120°B．105°C．60°D．45°
6．（2021秋•雨花区校级期中）如图，在△ABC中，点D在CB的延长线上，∠A＝70°，∠C＝50°，则∠ABD等于（ ）
A．100°B．110°C．120°D．130°
7．（2021秋•宣化区期中）如图，已知△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A．90°B．135°C．270°D．315°
8．（2021春•遂宁期末）如图所示，∠1+∠2+∠3+∠4+∠5+∠6＝ ．
9．如图，小明从A点出发，沿直线前进6米后向左转45°，再沿直线前进6米，又向左转45°…照这样走下去，他第一次回到出发点A时，共走路程为（ ）米．
A．60B．72C．48D．36
10．（2015秋•洪山区期中）若一个多边形的内角和度数为外角和的4倍，则这个多边形的边数为（ ）
A．12B．10C．9D．8
二、填空题
11．（2022秋•博罗县期中）n边形的每个外角为30°，则边数n的值是 ．
12．（2021秋•雨花区校级期中）正十边形的每个外角的大小是 度．
13．（2021秋•城西区校级期中）一个八边形的所有内角都相等，它的每一个外角等于 度．
14．（2019秋•越秀区校级期中）正多边形的一个内角等于144°，则该多边形是正 边形．
15．（2021秋•宣化区期中）从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是 ．
三、解答题
16．（2021春•重庆期末）如图所示，已知AD，AE分别是△ADC和△ABC的高和中线，AB＝6cm，AC＝8cm，BC＝10cm，∠CAB＝90°．试求：
（1）AD的长；
（2）△ABE的面积；
（3）△ACE和△ABE的周长的差．
17．（2021秋•宣化区期中）如图，在△ABC中，AB＞AC，AD为BC边上的中线．
（1）S△ABD S△ACD（填“＞”、“＜”或“＝”）；
（2）若△ABD的周长比△ACD的周长多4，且AB+AC＝14，求AB，AC的长．
18．（2021春•内江期末）如图，在△ABC中，∠B＝31°，∠C＝55°，AD⊥BC于D，AE平分∠BAC交BC于E，DF⊥AE于F，求∠ADF的度数．
19.（平昌县期末）如图，△ACB中，∠ACB＝90°，∠1＝∠B．
（1）试说明CD是△ABC的高；
（2）如果AC＝8，BC＝6，AB＝10，求CD的长．
20.（2021春•薛城区期末）已知某正多边形的一个内角都比它相邻外角的3倍还多20°．
（1）求这个正多边形一个内角的度数；
（2）求这个正多边形的内角和．
专题01 三角形（基础精炼卷）
一、选择题（共10题）
1．（2022秋•博罗县期中）下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（ ）
A．2，2，4B．3，2，6C．1，2，2D．1，2，3
【答案】C
【解答】解：A、2+2＝4，不能摆成三角形；
B、2+3＜6，不能摆成三角形；
C、1+2＞2，能摆成三角形；
D、1+2＝3，不能摆成三角形．
故选：C．
2．（2022秋•博罗县期中）如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（ ）
A．三角形的稳定性B．两点之间线段最短
C．两点确定一条直线D．垂线段最短
【答案】A
【解答】解：根据三角形的稳定性可固定窗户．
故选：A．
3．（2022秋•博罗县期中）下面四个图形中，线段BE是△ABC的高的图是（ ）
A．B．
C．D．
【答案】D
【解答】解：A选项中，BE与AC不垂直；
B选项中，BE与AC不垂直；
C选项中，BE与AC不垂直；
∴线段BE是△ABC的高的图是D选项．
故选：D．
4．（2021秋•城西区校级期中）如果三角形的三个内角的度数比是2：3：4，则它是（ ）
A．锐角三角形B．钝角三角形
C．直角三角形D．钝角或直角三角形
【答案】A
【解答】解：设三个内角分别为2k、3k、4k，
则2k+3k+4k＝180°，
解得k＝20°，
所以，最大的角为4×20°＝80°，
所以，三角形是锐角三角形．
故选：A．
5．（2022秋•博罗县期中）如果将一副三角板按如图方式叠放，那么∠1等于（ ）
A．120°B．105°C．60°D．45°
【答案】B
【解答】解：如图，∠2＝90°﹣45°＝45°，
由三角形的外角性质得，∠1＝∠2+60°，
＝45°+60°，
＝105°．
故选：B．
6．（2021秋•雨花区校级期中）如图，在△ABC中，点D在CB的延长线上，∠A＝70°，∠C＝50°，则∠ABD等于（ ）
A．100°B．110°C．120°D．130°
【答案】C
【解答】解：∵∠ABD是△ABC的外角，∠A＝70°，∠C＝50°，
∴∠ABD＝∠A+∠C＝70°+50°＝120°．
故选：C．
7．（2021秋•宣化区期中）如图，已知△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A．90°B．135°C．270°D．315°
【答案】C
【解答】解：∵四边形的内角和为360°，直角三角形中两个锐角和为90°
∴∠1+∠2＝360°﹣（∠A+∠B）＝360°﹣90°＝270°．
故选：C．
8．（2021春•遂宁期末）如图所示，∠1+∠2+∠3+∠4+∠5+∠6＝ ．
【答案】360°
【解答】解：如图，∵∠1+∠5＝∠7，∠4+∠6＝∠8，
又∵∠2+∠3+∠7+∠8＝360°，
∴∠1+∠2+∠3+∠4+∠5+∠6＝360°．
故答案为：360°．
9．如图，小明从A点出发，沿直线前进6米后向左转45°，再沿直线前进6米，又向左转45°…照这样走下去，他第一次回到出发点A时，共走路程为（ ）米．
A．60B．72C．48D．36
【答案】C
【解答】解：根据题意可知，他需要转360÷45＝8次才会回到原点，
所以一共走了8×6＝48（米）．
故选：C．
10．（2015秋•洪山区期中）若一个多边形的内角和度数为外角和的4倍，则这个多边形的边数为（ ）
A．12B．10C．9D．8
【答案】B
【解答】解：设这个多边形的边数为n，
（n﹣2）•180°＝4×360°，
解得n＝10，
故选：B．
二、填空题
11．（2022秋•博罗县期中）n边形的每个外角为30°，则边数n的值是 ．
【答案】12
【解答】解：n＝360°÷30°＝12，
故答案为：12．
12．（2021秋•雨花区校级期中）正十边形的每个外角的大小是 度．
【答案】36
【解答】解：∵正多边形的每个外角相等，
∴正十边形每个外角为360°÷10＝36°．
故答案为：36．
13．（2021秋•城西区校级期中）一个八边形的所有内角都相等，它的每一个外角等于 度．
【答案】45
【解答】解：∵一个八边形的所有内角都相等，
∴这个八边形的所有外角都相等，
∴这个八边形的所有外角＝＝45°，
故答案为45；
14．（2019秋•越秀区校级期中）正多边形的一个内角等于144°，则该多边形是正 边形．
【答案】十
【解答】解：设正多边形是n边形，由题意得
（n﹣2）×180°＝144°n．
解得n＝10，
故答案为：十．
15．（2021秋•宣化区期中）从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是 ．
【答案】8【解答】解：设多边形有n条边，
则n﹣2＝6，
解得n＝8．
故答案为：8．
三、解答题
16．（2021春•重庆期末）如图所示，已知AD，AE分别是△ADC和△ABC的高和中线，AB＝6cm，AC＝8cm，BC＝10cm，∠CAB＝90°．试求：
（1）AD的长；
（2）△ABE的面积；
（3）△ACE和△ABE的周长的差．
【答案】（1）AD的长度为4.8cm （2）△ABE的面积是12cm2．（3）2cm
【解答】解：∵∠BAC＝90°，AD是边BC上的高，
∴AB•AC＝BC•AD，
∴AD＝＝＝4.8（cm），即AD的长度为4.8cm；
（2）方法一：如图，∵△ABC是直角三角形，∠BAC＝90°，AB＝6cm，AC＝8cm，
∴S△ABC＝AB•AC＝×6×8＝24（cm2）．
又∵AE是边BC的中线，
∴BE＝EC，
∴BE•AD＝EC•AD，即S△ABE＝S△AEC，
∴S△ABE＝S△ABC＝12（cm2）．
∴△ABE的面积是12cm2．
方法二：因为BE＝BC＝5，由（1）知AD＝4.8，
所以S△ABE＝BE•AD＝×5×4.8＝12（cm2）．
∴△ABE的面积是12cm2．
（3）∵AE为BC边上的中线，
∴BE＝CE，
∴△ACE的周长﹣△ABE的周长＝AC+AE+CE﹣（AB+BE+AE）＝AC﹣AB＝8﹣6＝2（cm），即△ACE和△ABE的周长的差是2cm．
17．（2021秋•宣化区期中）如图，在△ABC中，AB＞AC，AD为BC边上的中线．
（1）S△ABD S△ACD（填“＞”、“＜”或“＝”）；
（2）若△ABD的周长比△ACD的周长多4，且AB+AC＝14，求AB，AC的长．
【解答】解：（1）过A点作AM⊥BC于M，
∵AD为BC边上的中线，
∴BD＝CD，
∵S△ABD＝BD•AM，S△ACD＝CD•AM，
∴S△ABD＝S△ACD，
故答案为：＝；
（2）∵BD＝CD，
∴△ABD的周长﹣△ADC的周长＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC＝4，
即AB﹣AC＝4①，
又AB+AC＝14②，
①+②得．2AB＝18，
解得AB＝9，
②﹣①得，2AC＝10，
解得AC＝5，
∴AB和AC的长分别为：AB＝9，AC＝5．
18．（2021春•内江期末）如图，在△ABC中，∠B＝31°，∠C＝55°，AD⊥BC于D，AE平分∠BAC交BC于E，DF⊥AE于F，求∠ADF的度数．
【答案】∠ADF＝78°
【解答】解：∵∠B＝31°，∠C＝55°，
∴∠BAC＝94°，
∵AE平分∠BAC，
∴∠BAE＝∠BAC＝47°，
∴∠AED＝∠B+∠BAE＝31°+47°＝78°，
∵AD⊥BC，DF⊥AE，
∴∠EFD＝∠ADE＝90°，
∴∠AED+∠EDF＝∠EDF+∠ADF，
∴∠ADF＝∠AED＝78°．
19.（2019春•平昌县期末）如图，△ACB中，∠ACB＝90°，∠1＝∠B．
（1）试说明CD是△ABC的高；
（2）如果AC＝8，BC＝6，AB＝10，求CD的长．
【答案】（1）略 （2）CD＝．
【解答】解：（1）∵∠1+∠BCD＝90°，∠1＝∠B
∴∠B+∠BCD＝90°
∴△BDC是直角三角形，即CD⊥AB，
∴CD是△ABC的高；
（2）∵∠ACB＝∠CDB＝90°
∴S△ABC＝AC•BC＝AB•CD，
∵AC＝8，BC＝6，AB＝10，
∴CD＝＝＝．
20.（2021春•薛城区期末）已知某正多边形的一个内角都比它相邻外角的3倍还多20°．
（1）求这个正多边形一个内角的度数；
（2）求这个正多边形的内角和．
【答案】（1）140° （2）1260°
【解答】解：（1）设这个正多边形的一个外角的度数为x°，
根据题意得180﹣x＝3x+20，解得x＝40，
180°﹣x°＝140°，
所以这个正多边形一个内角的度数140°；
（2）因为这个正多边形的一个外角的度数为40°，
所以这个正多边形边数＝360°÷40°＝9，
所以这个正多边形的内角和是（9﹣2）×180°＝1260°．