人教版数学七上期末提升训练专题13 角综合运算（专题测试）（2份，原卷版+解析版）

这是一份人教版数学七上期末提升训练专题13 角综合运算（专题测试）（2份，原卷版+解析版），文件包含人教版数学七上期末提升训练专题13角综合运算专题测试原卷版doc、人教版数学七上期末提升训练专题13角综合运算专题测试解析版doc等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
选择题（每小题3分，共30分）
1．（2022春•周村区期末）若∠A＝53°17'，则∠A的余角的度数为（ ）
A．36°43'B．46°43'C．36°17'D．46°17'
【答案】A
【解答】解：∵∠A＝53°17′，
∴∠A的余角＝90°﹣53°17′＝89°60′﹣53°17′＝36°43′．
故选：A．
2.（2022春•文登区校级期中）∠O，∠AOB，∠1表示同一角是（ ）
A．B．
C．D．
【答案】C
【解答】解：A、图中的∠AOB不能用∠O表示，故本选项错误；
B、图中的∠AOB不能用∠O表示，故本选项错误；
C、图中∠1、∠AOB、∠O表示同一个角，故本选项正确；
D、图中的∠1不能用∠O表示，故本选项错误；
故选：C
3．（2022春•乳山市期末）已知∠α＝35°，则∠α的补角度数是（ ）
A．145°B．95°C．65°D．55°
【答案】A
【解答】解：∵∠α＝35°，
∴∠α的补角度数是180°﹣α＝180°﹣35°＝145°．
故选：A．
4．（2021秋•肥东县期末）互为补角的两个角的比是3：2，则较小角的余角等于（ ）
A．18°B．54°C．108°D．144°
【答案】A
【解答】解：∵互为补角的两个角的比是3：2，
∴较大的角＝180°×＝108°，较小的角＝180°×＝72°，
∴较小角的余角＝90°﹣72°＝18°，
故选：A．
5．（2021秋•威县期末）如图，∠AOB＝20°，∠BOC＝80°，OE是∠AOC的角平分线，则∠COE的度数为（ ）
A．50°B．40°C．30°D．20°
【答案】A
【解答】解：∵∠AOB＝20°，∠BOC＝80°，
∴∠AOC＝∠AOB+∠BOC＝100°
而OE是∠AOC的角平分线，
∴∠COE＝∠AOC＝50°
故选：A．
6．下列判断中，正确的是（ ）
①锐角的补角一定是钝角；
②一个角的补角一定大于这个角；
③如果两个角是同一个角的补角，那么它们相等；
④锐角和钝角互补．
A．①②B．①③C．①④D．②③
【答案】B
【解答】解：①锐角的补角一定是钝角，说法正确；
②一个角的补角一定大于这个角，说法错误例如90°角的补角；
③如果两个角是同一个角的补角，那么它们相等，说法正确；
④锐角和钝角互补，说法错误，例如60°角和100°角，
正确的说法有2个，是①③，
故选：B．
7．（2022春•东营期末）如图，OC平分∠AOB，OD平分∠BOC，下列各式正确的是（ ）
A．B．
C．∠BOC＝∠AODD．
【答案】C
【解答】解：∵OC平分∠AOB，
∴∠BOC＝∠AOC＝∠AOB，
∵OD平分∠BOC，
∴∠BOD＝∠COD＝∠BOC，
∴∠COD＝∠AOB，
故A选项不符合题意；
∵∠AOD＝∠AOC+∠COD＝3∠BOD，
∴∠BOD＝∠AOD，
故B选项不符合题意；
∴∠BOC＝∠AOD，
故C选项符合题意；
∵∠AOB＝4∠BOD，∠AOD＝3∠BOD，
∴∠AOD＝∠AOB，
故D选项不符合题意；
故选：C
8．如图，将一副三角尺按不同的位置摆放，下列方式中∠α与∠β互余的是（ ）
A．图①B．图②C．图③D．图④
【答案】A
【解答】解：图①，∠α+∠β＝180°﹣90°＝90°，互余；
图②，根据同角的余角相等，∠α＝∠β；
图③，根据等角的补角相等∠α＝∠β；
图④，∠α+∠β＝180°，互补．
故选：A．
9.（2021秋•双牌县期末）若∠A＝32°18′，∠B＝32°15′30″，∠C＝32.25°，则（ ）
A．∠A＞∠B＞∠CB．∠B＞∠A＞∠CC．∠A＞∠C＞∠BD．∠C＞∠A＞∠B
【答案】A
【解答】解：∵1°＝60′；
∴0.25°＝60′×0.25＝15′；
∴∠C＝32°15′；
∴32°18′＞32°15′30″＞32°15′；
∴∠A＞∠B＞∠C．
故选：A．
10．（2022春•泰安期末）如图所示，∠AOB是平角，OC是射线，OD、OE分别是∠AOC、∠BOC的角平分线，若∠COE＝28°，则∠AOD的度数为（ ）
A．56°B．62°C．72°D．124°
【答案】B
【解答】解：∵OE平分∠BOC，
∴∠BOC＝2∠COE＝56°．
∴∠AOC＝180°﹣∠BOC＝124°．
∵OD平分∠AOC，
∴∠AOD＝∠COD＝∠AOC＝62°．
故选：B．
填空题（每小题3分，共15分）
11．钟表分针的运动可看作是一种旋转现象，一只标准时钟的分针匀速旋转，经过15分钟旋转了 度．
【答案】９０
【解答】解：如图，15分钟分针转过了3个大格，每个大格30°，共转了30°×3＝90°．
12．（2022春•锦江区校级期中）如图，∠COD＝28°，若∠AOB与∠COD互余，则∠AOB＝ .若B、O、C在同一条直线上，则∠BOD＝ ．
【答案】62°，152°
【解答】解：∵∠AOB与∠COD互余，
∴∠AOB+∠COD＝90°，
∵∠COD＝28°，
∴∠AOB＝90°﹣∠COD＝90°﹣28°＝62°；
∵B、O、C在同一条直线上，
∴∠BOD+∠COD＝180°，
∴∠BOD＝180°﹣∠COD＝180°﹣28°＝152°．
故答案为：62°，152°
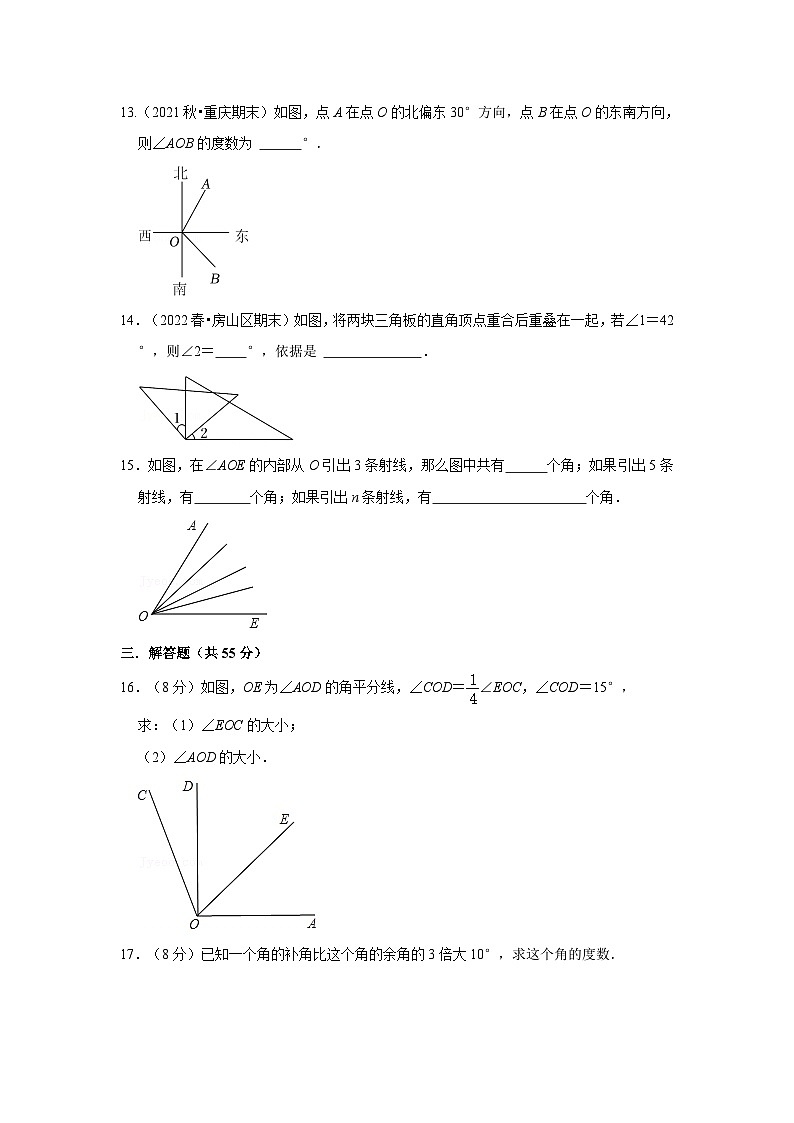
13.（2021秋•重庆期末）如图，点A在点O的北偏东30°方向，点B在点O的东南方向，则∠AOB的度数为 °．
【答案】105．
【解答】解：∵点B在点O的东南方向，
∴点B在点O的南偏东45°方向，
∴∠AOB＝180°﹣30°﹣45°＝105°．
故答案为：105．
14．（2022春•房山区期末）如图，将两块三角板的直角顶点重合后重叠在一起，若∠1＝42°，则∠2＝ °，依据是 ．
【答案】42，同角或等角的余角相等．
【解答】解：如图，
∵∠1+∠3＝90°，∠2+∠3＝90°，
∴∠1＝∠2＝42°．
依据是同角或等角的余角相等．
故答案为：42，同角或等角的余角相等．
15．如图，在∠AOE的内部从O引出3条射线，那么图中共有 个角；如果引出5条射线，有 个角；如果引出n条射线，有 个角．
【答案】１０，２１，（n+1）（n+2）
【解答】解：引出3条射线，那么图中共有10个角；如果引出5条射线，有21个角；如果引出n条射线，有（n+1）（n+2）个角．
三．解答题（共55分）
16．（8分）如图，OE为∠AOD的角平分线，∠COD＝∠EOC，∠COD＝15°，
求：（1）∠EOC的大小；
（2）∠AOD的大小．
【解答】解：（1）∵∠COD＝∠EOC＝15°，
∴∠EOC＝60°；
（2）∵∠DOE＝∠EOC＝45°，
∴∠AOD＝2∠DOE＝90°．
故答案为：60°，90°．
17．（8分）已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．
【解答】解：设这个角是x，则（180°﹣x）﹣3（90°﹣x）＝10°，
解得x＝50°．
故答案为50°．
18．（8分）如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠AOC和∠COB的度数．
【解答】解：∵OE平分∠AOB，OF平分∠BOC，
∴∠BOE＝∠AOB＝×90°＝45°，∠COF＝∠BOF＝∠BOC，
∵∠BOF＝∠EOF﹣∠BOE＝60°﹣45°＝15°，
∴∠BOC＝2∠BOF＝30°；
∠AOC＝∠BOC+∠AOB＝30°+90°＝120°．
19．(10分）如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC．
（1）指出图中∠AOD与∠BOE的补角；
（2）试说明∠COD与∠COE具有怎样的数量关系．
【解答】解：（1）与∠AOD互补的角∠BOD、∠COD；
与∠BOE互补的角∠AOE、∠COE．
（2）∠COD+∠COE＝∠AOB＝90度．（提示：因为OD平分∠BOC，所以∠COD＝∠BOC）．
又OE平分∠AOC，所以∠COE＝∠AOC，
所以∠COD+∠COE＝∠BOC+∠AOC＝（∠BOC+∠AOC），
所以∠COD+∠COE＝∠AOB＝90°．
20．（10分）把一副三角板的直角顶点O重叠在一起．
（1）如图（1），当OB平分∠COD时，则∠AOD与∠BOC的和是多少度？
（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？
（3）当∠BOC的余角的4倍等于∠AOD，则∠BOC多少度？
【解答】解：（1）当OB平分∠COD时，有∠BOC＝∠BOD＝45°，
于是∠AOC＝90°﹣45°＝45°，
所以∠AOD+∠BOC＝∠AOC+∠COD+∠BOC＝45°+90°+45°＝180°；
（2）当OB不平分∠COD时，
有∠AOB＝∠AOC+∠BOC＝90°，∠COD＝∠BOD+∠BOC＝90°，
于是∠AOD+∠BOC＝∠AOC+∠BOC+∠BOD+∠BOC，
所以∠AOD+∠BOC＝90°+90°＝180°．
（3）由上得∠AOD+∠BOC＝180°，
有∠AOD＝180°﹣∠BOC，
180°﹣∠BOC＝4（90°﹣∠BOC），
所以∠BOC＝60°．
21．（11分）以直线AB上点O为端点作射线OC，使∠BOC＝60°，将直角△DOE的直角顶点放在点O处．
（1）如图1，若直角△DOE的边OD放在射线OB上，则∠COE＝ 30° ；
（2）如图2，将直角△DOE绕点O按逆时针方向转动，使得OE平分∠AOC，说明OD所在射线是∠BOC的平分线；
（3）如图3，将直角△DOE绕点O按逆时针方向转动，使得∠COD＝∠AOE．求∠BOD的度数．
【解答】解：（1）∵∠BOE＝∠COE+∠COB＝90°，
又∵∠COB＝60°，
∴∠COE＝30°，
故答案为：30°；
（2）∵OE平分∠AOC，
∴∠COE＝∠AOE＝COA，
∵∠EOD＝90°，
∴∠AOE+∠DOB＝90°，∠COE+∠COD＝90°，
∴∠COD＝∠DOB，
∴OD所在射线是∠BOC的平分线；
（3）设∠COD＝x°，则∠AOE＝5x°，
∵∠DOE＝90°，∠BOC＝60°，
∴6x＝30或5x+90﹣x＝120
∴x＝5或7.5，
即∠COD＝5°或7.5°
∴∠BOD＝65°或52.5°．