湖北省随州市随县四校联考2024-2025学年九年级上学期11月月考数学试题（原卷版）-A4

这是一份湖北省随州市随县四校联考2024-2025学年九年级上学期11月月考数学试题（原卷版）-A4，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
时间：120分钟 总分：120分
一、选择题（共10小题，每小题3分，共30分）
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A B.
C. D.
2. 用配方法解一元二次方程时，原方程可变形为（ ）
A B. C. D.
3. 一元二次方程的根的情况是（ ）
A. 有两个不相等的实数根B. 没有实数根
C. 有两个相等的实数根D. 无法确定
4. 下列说法正确的是( )
A. 三点确定一个圆
B. 一个三角形只有一个外接圆
C. 和半径垂直的直线是圆的切线
D. 三角形的内心到三角形三个顶点距离相等
5. 把抛物线向左平移1个单位，然后向上平移2个单位，则平移后抛物线的表达式是( )
A. B. C. D.
6. 毕业在即，初三某毕业班每一个同学都向其他同学曾送一张自己的照片留作纪念，全班共送了张照片，若该班有名同学，则根据题意可列出方程为（ ）
A. B.
C. D.
7. 已知二次函数的图像经过点和点，则下列关系式正确的是（ ）
A. B. C. D.
8. 如图，AB是的直径，弦于点E，，则的度数为（ ）
A. B. C. D.
9. 如图，在中，，边与轴平行且，现将以为旋转中心，逆时针旋转，每次旋转，则经过次旋转后，点的坐标为（ ）
A. B. C. D.
10. 二次函数的图象如图所示，对称轴为直线，给出下列结论：①；②当时，；③；④，其中正确的结论有（ ）个
A. 个B. 个C. 个D. 个
二、填空题（共5小题，每小题3分，共15分）
11. 点关于原点中心对称的的坐标为___________．
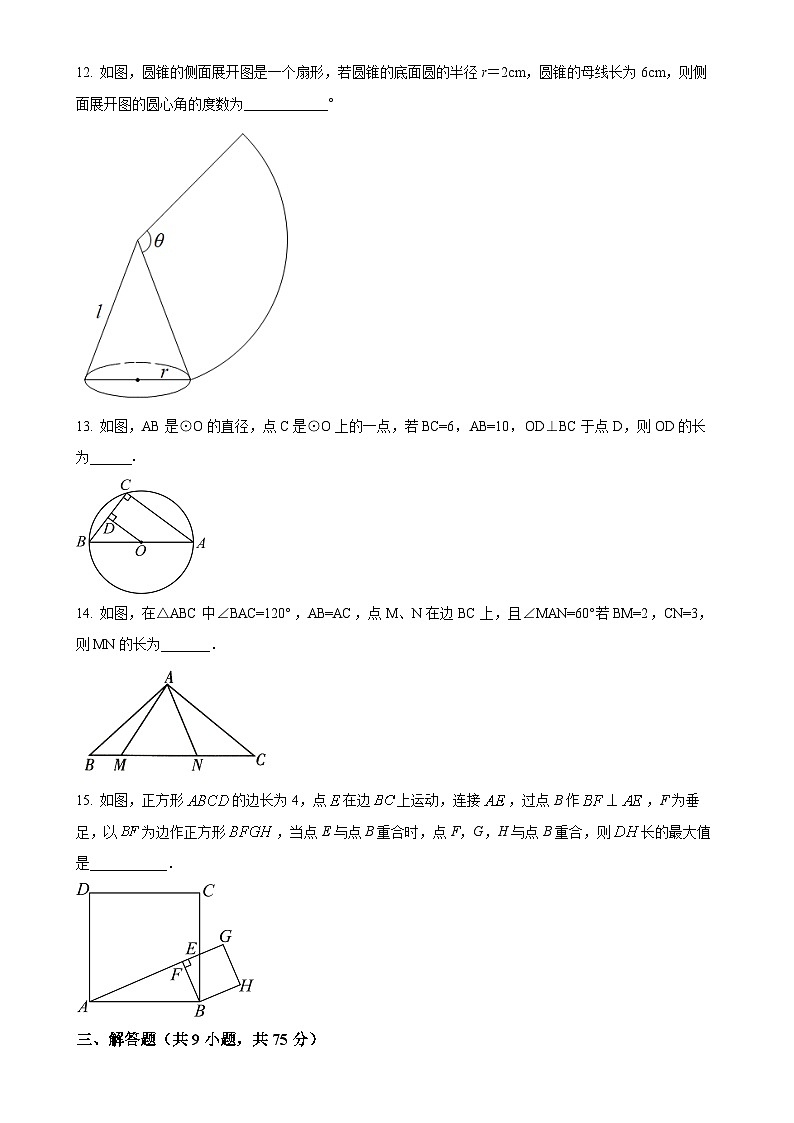
12. 如图，圆锥的侧面展开图是一个扇形，若圆锥的底面圆的半径r＝2cm，圆锥的母线长为6cm，则侧面展开图的圆心角的度数为____________°
13. 如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=6，AB=10，OD⊥BC于点D，则OD的长为______．
14. 如图，在△ABC中∠BAC=120°，AB=AC，点M、N在边BC上，且∠MAN=60°若BM=2，CN=3，则MN的长为_______．
15. 如图，正方形的边长为4，点在边上运动，连接，过点B作，F为垂足，以为边作正方形，当点E与点B重合时，点F，G，H与点B重合，则长的最大值是___________．
三、解答题（共9小题，共75分）
16. 解下列方程
（1）
（2）
17. 已知关于的一元二次方程
（1）求证：无论取何实数值，方程总有实数根；
（2）若的一边长，另两边长恰好是这个方程的两个根，求的取值范围．
18. 如图，在中，，将绕点A顺时针旋转得到使点C的对应点E落在上，连接．
（1）若，求的度数；
（2）若，求的长．
19. 抛物线与轴交于、两点（在左侧），与轴交于点，过，两点的直线．
（1）点的坐标为___________，点的坐标为___________．
（2）抛物线顶点坐标为___________．
（3）当时，自变量x的取值范围是___________．
（4）当时，求取值范围．
20. 如图，用长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，为了方便出入，在建造篱笆花圃时，在BC上用其他材料做了宽为1米的两扇小门．
（1）设花圃的一边AB长为x米，请你用含x的代数式表示另一边AD的长为 米；
（2）若此时花圃的面积刚好为45m2，求此时花圃的长与宽．
21. 如图，是直径，是的弦，，垂足为H，过点C作直线分别于的延长线交于点E，F， 且．
（1）求证：是的切线；
（2）若，求的长．
22. 一大型商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元件）（x为正整数）之间满足一次函数关系，下表记录的是某三周的有关数据：
（1）求y与x的函数关系式（不求自变量的取值范围）；
（2）在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？
（3）抗疫期间，该商场这种商品售价不大于15元/件时，每销售一件商品便向某慈善机构捐赠m元（），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．
23. 将正方形和正方形如图1摆放，使D点在边上，M为中点，
（1）连接，，则容易发现，间的关系是___________；
（2）操作：如图2，把正方形绕C点顺时针旋转，使对角线放在正方形的边的延长线上，取线段的中点M，探究线段，的关系，并加以说明
（3）将正方形绕点C顺时针旋转任意角度后（如图3），其他条件不变，（2）中的结论是否仍成立？直接写出猜想，并加以证明．
24. 综合与探究
如图，抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接．若点P在线段上运动（点P不与点重合），过点P作x轴的垂线，交抛物线于点E，交x轴于点F．设点P的横坐标为m．
（1）求点A，B，C的坐标，并直接写出直线的函数解析式．
（2）若，求m的值．
x（元/件）
4
5
6
y（件）
10000
9500
9000