山东省青岛市胶州实验初级中学2024-2025学年上学期九年级数学10月月考试卷（解析版）-A4

这是一份山东省青岛市胶州实验初级中学2024-2025学年上学期九年级数学10月月考试卷（解析版）-A4，共20页。试卷主要包含了选择题，填空题，作图题，解答题等内容，欢迎下载使用。
一、选择题（每小题3分，共24分）
1. 方程根的情况是（ ）
A. 有两个相等的实数根B. 有两个不相等的实数根C. 没有实数根D. 有一个实数根
【答案】B
【解析】
【分析】先计算根的判别式，再对方程根的情况进行判断 ．
【详解】解：，
∴方程有两个不相等的实数根．
故选：B．
【点睛】本题考查一元二次方程根的判别式，熟练掌握根的判别式计算公式及其与方程根情况的联系是解题关键．
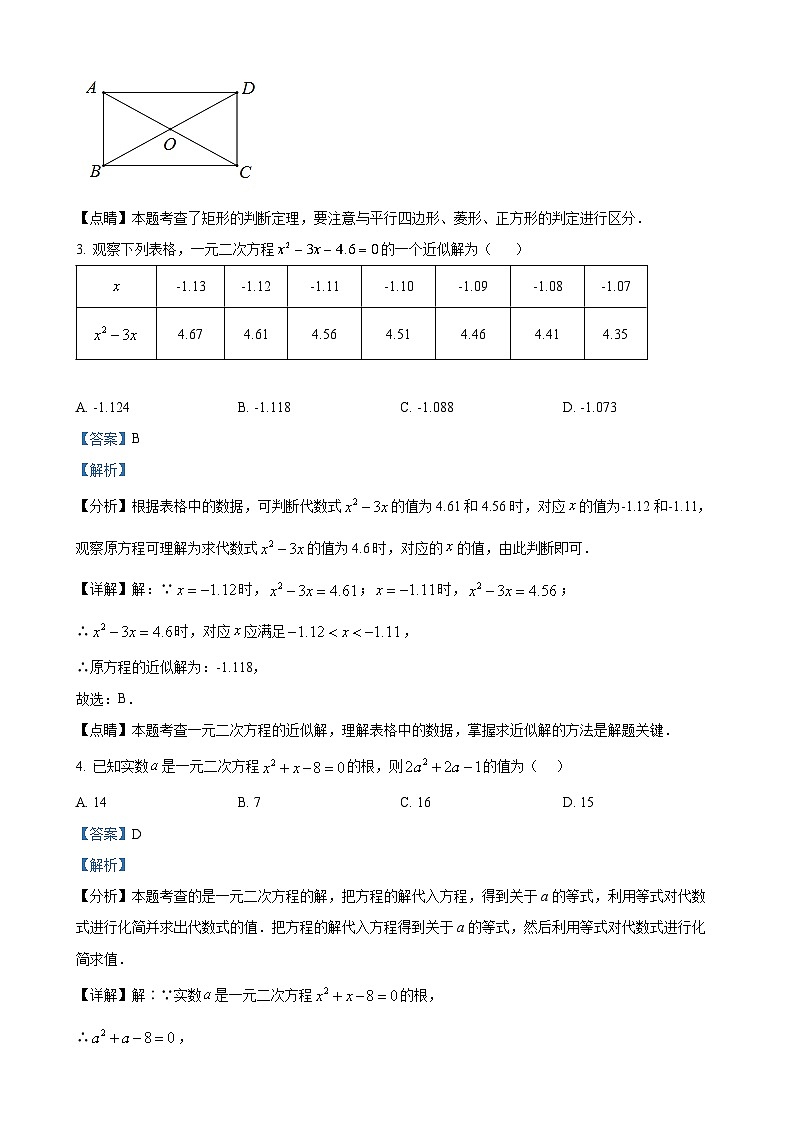
2. 四边形ABCD的对角线AC，BD相交于点O，能判定它是矩形的是（ ）．
A. ，B. ，
C. ，，D.
【答案】D
【解析】
【分析】A、对角线互相平分是平行四边形的判断定理；
B、邻边相等，O是对角线AC中点，无法判定是矩形；
C、对角线互相垂直平分是菱形的判定定理；
D、对角线互相平分且相等，可以判定是矩形．
【详解】A、已知对角线互相平分，可以判定是平行四边形，不符合题意；
B、已知邻边相等，O是对角线AC中点，无法判定是矩形，不符合题意；
C、已知对角线互相垂直平分，可以判定是菱形，不符合题意；
D、已知对角线互相平分且相等，可以判定是矩形，符合题意；
故选D．
【点睛】本题考查了矩形的判断定理，要注意与平行四边形、菱形、正方形的判定进行区分．
3. 观察下列表格，一元二次方程的一个近似解为（ ）
A. -1.124B. -1.118C. -1.088D. -1.073
【答案】B
【解析】
【分析】根据表格中的数据，可判断代数式的值为4.61和4.56时，对应的值为-1.12和-1.11，观察原方程可理解为求代数式的值为4.6时，对应的的值，由此判断即可．
【详解】解：∵时，；时，；
∴时，对应应满足，
∴原方程的近似解为：-1.118，
故选：B．
【点睛】本题考查一元二次方程的近似解，理解表格中的数据，掌握求近似解的方法是解题关键．
4. 已知实数是一元二次方程的根，则的值为（ ）
A. 14B. 7C. 16D. 15
【答案】D
【解析】
【分析】本题考查的是一元二次方程的解，把方程的解代入方程，得到关于a的等式，利用等式对代数式进行化简并求出代数式的值．把方程的解代入方程得到关于a的等式，然后利用等式对代数式进行化简求值．
【详解】解∶∵实数是一元二次方程的根，
∴，
∴，
∴，
故选∶D．
5. 已知关于x的方程的两个实数根互为相反数，则a的值为（ ）
A. 5或B. 0C. 5D.
【答案】C
【解析】
【分析】本题主要考查了一元二次方程根与系数的关系，解一元二次方程，设关于x的方程的两个实数根为，则由根与系数的关系得到，，再由相反数的定义得到，，据此可得或，再由可得，则．
【详解】解：设关于x的方程的两个实数根为，
∴，
∵关于x的方程的两个实数根互为相反数，
∴，，
∴或，
∵，
∴，
∴，
∴，
故选：C．
6. 某经济技术开发区今年一月份工业产值达50亿元，且一月份、二月份、三月份的总产值为175亿元，若设平均每月的增长率为x，根据题意可列方程（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．增长率问题，一般用增长后的量增长前的量（增长率），本题可先用x表示出二月份的产值，再根据题意表示出三月份的产值，然后将三个月的产值相加，即可列出方程．
【详解】解：二月份的产值为：，
三月份的产值为：，
故第一季度总产值为：．
故选：D．
7. 如图所示，在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连接BE、AF相交于点G，则下列结论不正确的是（ ）
A. BE=AFB. ∠DAF=∠BEC
C. AG⊥BED. ∠AFB+∠BEC=90°
【答案】D
【解析】
【分析】分析图形，根据正方形及三角形性质找到各角边的关系即可求解．
【详解】解：∵ABCD是正方形
∴∠ABF＝∠C＝90°，AB＝BC
∵BF＝CE
∴△ABF≌△BCE
∴AF＝BE（A正确）
∵∠BFA＝∠BEC，
∴ ，
∵ ，
∴（D错误）
∵∠BAF＋∠DAF＝90°，∠BAF＋∠BFA＝90°
∴∠DAF＝∠BEC（B正确）
∵∠BAF＝∠CBE，∠BAF＋∠AFB＝90°
∴∠CBE＋∠AFB＝90°
∴AG⊥BE（C正确）
故选D．
【点睛】此题主要考查了学生对正方形的性质及全等三角形的判定的掌握情况．熟练掌握正方形的性质及全等三角形的判定是解题关键．
8. 在菱形中，对角线，相交于点，，，过点作的平行线交的延长线于点，则的面积为（ ）
A. 24B. 18C. 12D. 10
【答案】A
【解析】
【分析】先判断出四边形ACED是平行四边形，从而得出DE的长度，根据菱形的性质求出BD的长度，利用勾股定理的逆定理可得出△BDE是直角三角形，计算出面积即可．
【详解】解： 菱形ABCD，

在Rt△BCO中， 则BD=8，

∴四边形ACED是平行四边形，
∴AC=DE=6，
BE=BC+CE=10，

∴△BDE是直角三角形，
∴S△BDE=DE•BD=24．
故选：A．
【点睛】本题考查了菱形的性质，勾股定理的逆定理及三角形的面积，平行四边形的判定与性质，求出BD的长度，判断△BDE是直角三角形，是解答本题的关键．
二、填空题（每小题3分，共24分）
9. 方程化为一般形式后，它的各项系数之和是______．
【答案】
【解析】
【分析】此题考查一元二次方程，掌握一元二次方程的一般式是解题的关键．
首先将方程化为一般式，然后确定各项的系数，记住一定带上它前面的符号，接下来求和即可解答．
【详解】解：方程化成一般形式后为，
则各项系数为，
则各项系数之和为．
故答案为：．
10. 如图，矩形ABCD的对角线AC、BD相交于点O，，，若AB＝4，BC＝3，则四边形CODE的周长是________．
【答案】10
【解析】
【分析】根据矩形和勾股定理的性质，得；根据平行四边形的性质计算，即可得到答案．
【详解】∵矩形ABCD的对角线AC、BD相交于点O，AB＝4，BC＝3，
∴，
∴，
∵，，
∴四边形为平行四边形，
∴，，
∴四边形CODE的周长，
故答案为：10．
【点睛】本题考查了勾股定理、矩形、平行四边形的整式；解题的关键是熟练掌握矩形、勾股定理的性质，从而完成求解．
11. 如图，在菱形中，过点作分别交，于点，，为的中点，，则的度数为______．
【答案】##度
【解析】
【分析】本题考查菱形的性质及三角形内角和的应用，根据菱形的性质得出，，进而可判定，利用直角三角形斜边上的中线性质和等边对等角可得出，利用平行线的性质可得出，即可求解.
的内角和解答即可．
【详解】解：设，
∵四边形为菱形，
∴，，
∴，
∵，，
∴，
∵F为的中点．
∴，
∴，
∵，
∴，
∵，
∴，即，
解得：，
∴，
∵四边形为菱形，
∴．
故答案为：．
12. 如图，正方形的边长为，点在对角线BD上，且，，垂足为，则的长为______．
【答案】
【解析】
【分析】本题考查了正方形的性质、勾股定理、等腰直角三角形的性质、等腰三角形的判定，先由勾股定理求出，再求出，设，可得出方程，解方程即可．
【详解】解：设，
四边形是正方形，
，，，
，，
，
，
，
，
，
，
，
解得：，
即；
故答案为：．
13. 如图，点O是矩形的对角线的中点，点E为的中点．若，，则的周长为________．
【答案】
【解析】
【分析】先证明是中位线，则，利用直角三角形的性质得，从而得的长，利用勾股定理求得、的长，从而求出周长．
【详解】解：∵矩形，
∴，，
点是矩形对角线的中点，点E为的中点，
∴是的中位线，
．，
∴，
，，
，
，
，
在中，利用勾股定理求得．
周长为．
故答案为：．
【点睛】本题主要考查了矩形的性质，勾股定理，中位线的性质，直角三角形的性质，解题的技巧是把所求三角形的三条线段分别放在不同的三角形中求解长度．
14. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其它重要应用．
例如：求代数式x2+4x+5的最小值？解答过程如下：
解：x2+4x+5＝x2+4x+4+1＝（x+2）2+1．
∵（x+2）2≥0，
∴当x＝－2时，（x+2）2的值最小，最小值是0，
∴（x+2）2+1≥1，
∴当（x+2）2＝0时，（x+2）2+1的值最小，最小值是1，
∴x2+4x+5的最小值为1．
根据上述方法，可求代数式－x2－6x＋12有最_____（填“大”或“小”）值，为_________．
【答案】 ①. 大 ②. 21
【解析】
【分析】原式配方后，利用非负数的性质求出最大值即可．
【详解】解：﹣x2－6x+12
＝12﹣（x2＋6x）
＝12﹣（x2＋6x+9﹣9）
＝12﹣（x＋3）2＋9
＝21﹣（x＋3）2，
∵（x＋3）2≥0，
∴当（x＋3）2＝0时，21﹣（x＋3）2取得最大值21．
故答案为：大，21
【点睛】此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
15. 把长为，宽为的长方形硬纸板，剪掉2个小正方形和2个小长方形（阴影部分即剪掉的部分），把剩余部分折成一个有盖的长方体盒子，记剪掉的小的正方形边长为，（纸板的厚度忽略不计）若折成的长方体盒子表面积为，求此时长方体盒子的体积．
【答案】此时长方体盒子的体积为．
【解析】
【分析】此题考查了一元二次方程的应用．根据图示，可得，求出x的值，再根据长方体的体积公式列出算式，即可求出答案．
【详解】解：长方体盒子的长是：；
长方体盒子的宽是，即；
长方体盒子的高是；
根据题意，得：，
解得：（不合题意，舍去），
所以长方体盒子的体积．
答：此时长方体盒子的体积为．
16. 如图，将边长为3cm正方形ABCD绕顶点B逆时针旋转30°得到正方形EBCF，则两个图形重叠部分（阴影部分）的面积为______cm2．
【答案】33
【解析】
【分析】由正方形的性质和旋转的性质可得AB=BG，由“HL”可证Rt△ABM≌△GBM，可得∠ABM=∠GBM=30°，可求AM=，由可求阴影部分的面积．
【详解】解：如图，设AD与FG相交于点M，连接BM，
∵四边形ABCD是正方形，
∴AB=BC=3cm，∠ABC=90°，
∵正方形ABCD绕顶点B逆时针旋转30°得到正方形EBCF，
∴BG=BC，∠GBC=30°，
∴BG=AB，且BM=BM，
∴Rt△ABM≌△GBM（HL）
∴∠ABM=∠GBM，
∵∠ABM+∠GBM=∠ABC-∠GBC=60°
∴∠ABM=∠GBM=30°，
∵tan∠ABM=
∴AM=
∴S阴影=2×S△ABM=2××3×=3，
故答案为3
【点睛】本题考查了旋转的性质，正方形的性质，全等三角形判定和性质等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．
三、作图题（4分）
17. 如图所示，一块儿三角形空地ABC，要在其内部建一个菱形花园，使得B为菱形花园的一个顶点，其余3个顶点分别在的3条边上．请你能设计出此菱形花园．
【答案】见解析
【解析】
【分析】首先作的角平分线交AC于点D，再过点D分别作BC边和AB边的平行线，即可得出所求菱形．
【详解】解：如图所示，四边形BEDF为所求菱形，
作法：（1）作的角平分线交AC于点D，具体作法为：以点B为圆心，任意长为半径作圆，与AB边交于M点，与BC边交于N点，分别以M、N点为圆心，适当长为半径作圆，交于P点，作射线BP，交AC于点D；
（2）作交AB于点E，交BC于点F，则四边形BEDF为所求菱形．
证明：∵，，
∴四边形BEDF为平行四边形，
∵BD是的角平分线，
∴，
∵，
∴，
∴，
∴，
∴四边形BEDF为菱形．
【点睛】本题考查复杂作图，涉及角平分线的作法，平行线的性质，平行四边形的判定、菱形的判定等知识点，熟记菱形的判定方法是解题的关键．
四、解答题（共68分）
18. 解方程
（1）（配方法）
（2）（公式法）
（3）；
（4）；
【答案】（1），
（2），
（3），
（4），
【解析】
【分析】本题考查 了解一元二次方程，解题的关键是：
（1）利用配方法求解即可；
（2）利用公式法求解即可；
（3）化简后，利用配方法求解即可；
（4）利用因式分解法求解即可；
【小问1详解】
解∶ ，
，
，
，
，
∴，；
【小问2详解】
解：，
∴，
∴，
∴，；
【小问3详解】
解：，
化简，得，
∴，
∴，
∴，
∴，；
【小问4详解】
解：，
∴，
∴或，
∴，．
19. 已知关于的方程的一个根为1，求它的另一个根及的值．
【答案】，原方程的另一个根为．
【解析】
【分析】本题主要考查了一元二次方程解的定义，解一元二次方程，一元二次方程的解是使方程左右两边相等的未知数的值，据此把代入原说法求出m的值，进而解方程求出另一个根即可．
【详解】解：∵关于的方程的一个根为1，
∴，
解得，
∴原方程为，
整理得：，
∴，
解得或，
∴原方程的另一个根为．
20. 如图，某广场一角的矩形花草区，其长为，宽为，其间有三条等宽的路，一条直路，两条曲路，路以外的地方全部种上花草，要使花草的面积为，求路的宽度为_____．
【答案】
【解析】
【详解】设路的宽度是xm.根据题意，得
(40−2x)(26−x)=864，
x2−46x+88=0，
(x−2)(x−44)=0，
x=2或x=44(不合题意,应舍去).
故答案为2.
点睛：此题考查了一元二次方程实际应用，此类题目中注意利用平移的知识把道路平移到一块儿，对花草面积进行整体计算.
21. 如图，菱形中，，为中点，，于点，∥，交于点，交于点．
（1）求菱形的面积；
（2）求的度数．
【答案】(1) 菱形的面积是；
(2) °.
【解析】
【分析】连接AC，BD并且AC和BD相交于点O，根据菱形的性质以及垂直定理得到△ABC和△ADC都是正三角形，即AB=AC=4，再利用勾股定理求出BD的长，进而求出菱形ABCD的面积；根据正三角形的性质求出∠DAF的度数，然后利用三角形内角和定理求出∠CHA的度数．
【详解】(1)连结并且和相交于点，
∵,且平分，
∴ΔABC和都是正三角形，
∴，
因为ΔABO是直角三角形，
∴，
∴菱形的面积是．
(2) ∵是正三角形,，
∴°，
又∵∥，，
∴ 四边形是矩形，
∴°，
∴°
22. 如图，要利用一面墙（墙长为25米）建一个矩形场地，用97米长的围栏围成三个大小相同的矩形，每个矩形都有一个1米的门，设矩形的边长为米．
（1）请用含有的式子表示______（不要求写出的取值范围）；
（2）当为何值时，矩形场地的总面积为400平方米？
【答案】（1）
（2）
【解析】
【分析】本题考查了一元二次方程的应用，解题的关键是∶
（1）用围栏的长度加上3个门宽，再减去4个长求解即可；
（2）根据“矩形场地的总面积为400平方米”列方程求解即可．
【小问1详解】
解：，
故答案为：；
【小问2详解】
解：根据题意，得，
解得，，
当时，，不符合题意，舍去；
当时，，符合题意，
∴当时，矩形场地总面积为400平方米．
23. 某快餐店试销某种套餐，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．试销一段时间后发现，若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．若要使该店每天的利润为1560元，则每份套餐的售价应为多少元？
【答案】11或14元
【解析】
【分析】本题主要考查一元一次方程，一元二次方程的应用，分析题目中的数量关系，列出方程是解题的关键．
分类讨论，当售价（元）时；当售价（元）时，列方程求解即可．
【详解】解：设每份套餐售价应为x元
当售价（元）时，
根据题意，得，
解得（不符合题意，舍去）；
当售价（元）时，
根据题意，得，
解得，，
∴每份套餐的售价应定为11或14元，该店每天的利润为1560元．
24. 如图，在中，，，，点D从点C出发沿方向以的速度向点A匀速运动，同时点E从点A出发沿方向以的速度向点B匀速运动，当其中一个动点到达终点时，另一个动点也随之停止运动. 设点D，E运动的时间是，过点D作交于点F，连接，.

（1）当 时，， 时，为直角三角形?
（2）四边形能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由。
（3）请用含有t的式子表示的面积，并判断是否存在某一时刻t，使的面积是面积的，若存在，请求出t的值；若不存在，请说明理由。
【答案】（1）10；或12
（2）四边形能成为菱形，理由见解析
（3），当时，的面积是面积的
【解析】
【分析】（1）①根据直角三角形的性质可得，从而可得，求解即可；②分两种情况：当，根据直角三角形的性质可得；当时，根据直角三角形的性质可得，分别进行求解即可；
（2）证明四边形是平行四边形，再根据如果四边形是菱形，则必有邻边相等，即，列方程求解即可；
（3）根据四边形是平行四边形，可得，即可求得，再根据，列方程求解即可．
小问1详解】
解：①∵，，，
∴，
∵，
∴，
∵，则，，
当时，，
解得；
②当，则，
∴，
∴，
∵，，
∴，
解得，
当时，则，
∴，
∴，
∴，
解得，
综上所述，当或12时，为直角三角形，
故答案为：；或12；
【小问2详解】
解：四边形能成为菱形，理由如下：
由（1）可得，，，
∴，
∵，
∴四边形是平行四边形，
若四边形是菱形，则，
∴，
解得，
当时，四边形是菱形；
【小问3详解】
解：过点D作于点G，
由（1）可得，，，，
在中，，即，
由（2）可得，四边形是平行四边形，
∴，
∵，
∴，
∵，，
∴，
在中，，即，
∴，
当时，，
解得或（舍），
∴当时，的面积是面积的．
【点睛】本题考查直角三角形的性质、平行四边形的判定与性质、菱形的性质、锐角三角函数、解一元二次方程和一元一次方程，熟练掌握相关性质是解题的关键．
-1.13
-1.12
-1.11
-1.10
-1.09
-1.08
-1.07
4.67
4.61
4.56
4.51
4.46
4.41
4.35