陕西省西安国际港务区铁一中陆港初级中学2023-2024学年九年级上学期月考数学试题（原卷版）-A4

这是一份陕西省西安国际港务区铁一中陆港初级中学2023-2024学年九年级上学期月考数学试题（原卷版）-A4，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（时间：110分钟 总分：120分）
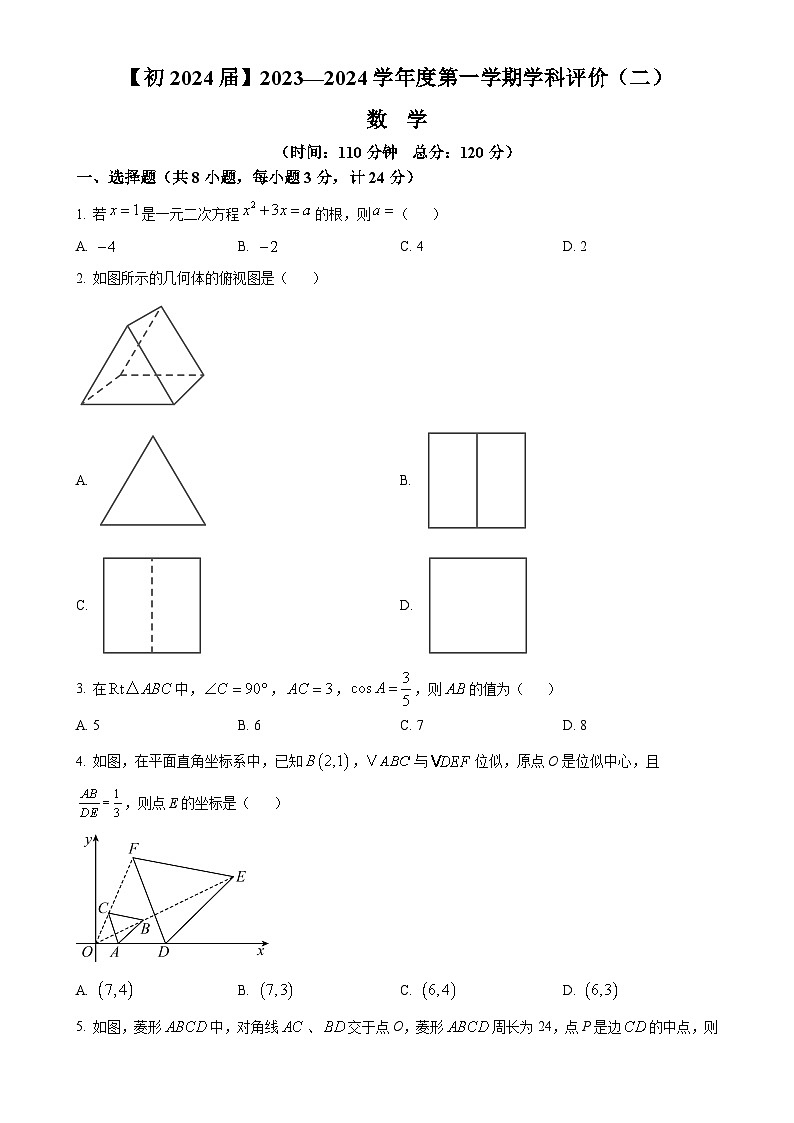
一、选择题（共8小题，每小题3分，计24分）
1. 若是一元二次方程的根，则（ ）
A. B. C. 4D. 2
2. 如图所示的几何体的俯视图是（ ）
A. B.
C. D.
3. 在中，，，，则的值为（ ）
A. 5B. 6C. 7D. 8
4. 如图，在平面直角坐标系中，已知，与位似，原点O是位似中心，且，则点E的坐标是（ ）
A. B. C. D.
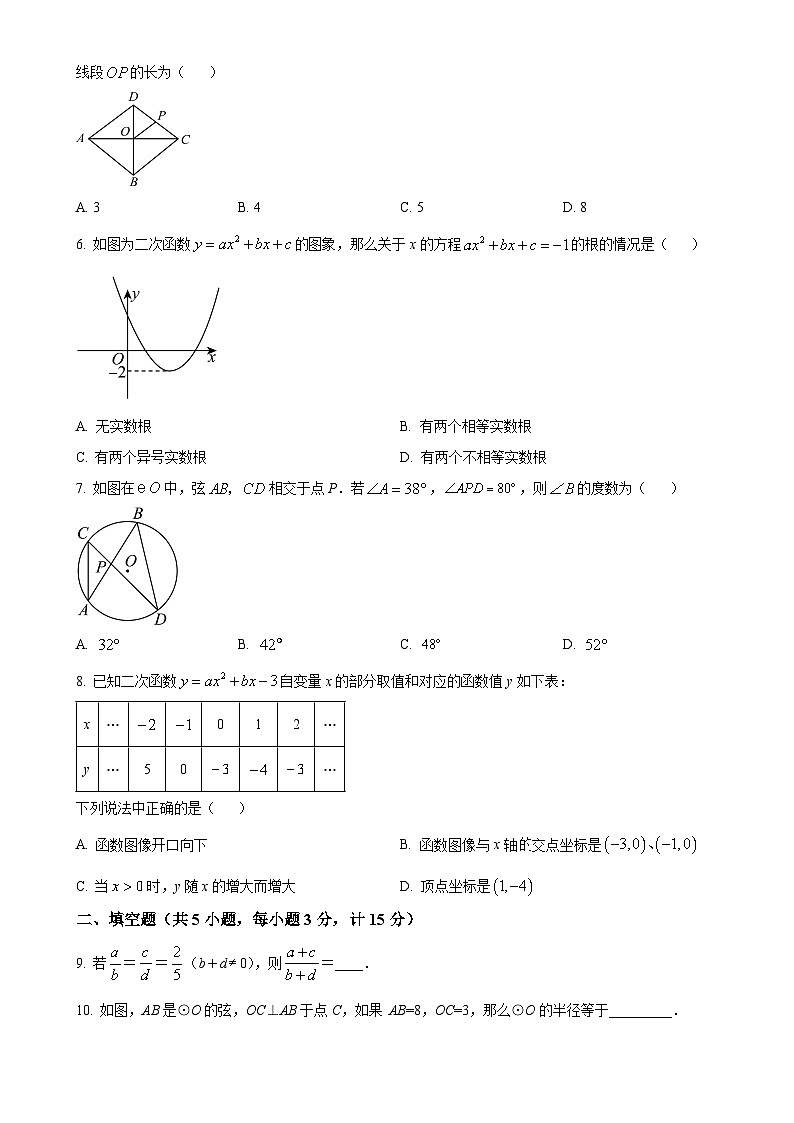
5. 如图，菱形中，对角线、交于点O，菱形周长为24，点P是边的中点，则线段的长为（ ）
A. 3B. 4C. 5D. 8
6. 如图为二次函数图象，那么关于x的方程的根的情况是（ ）
A. 无实数根B. 有两个相等实数根
C. 有两个异号实数根D. 有两个不相等实数根
7. 如图在中，弦相交于点P．若，，则的度数为（ ）
A. B. C. D.
8. 已知二次函数自变量x的部分取值和对应的函数值y如下表：
下列说法中正确的是（ ）
A. 函数图像开口向下B. 函数图像与x轴交点坐标是
C. 当时，y随x的增大而增大D. 顶点坐标是
二、填空题（共5小题，每小题3分，计15分）
9. 若＝＝（b＋d0），则＝____．
10. 如图，AB是⊙O的弦，OC⊥AB于点C，如果 AB=8，OC=3，那么⊙O的半径等于_________．
11. 如图所示的小孔成像实验中，若物距为，像距为，蜡烛火焰倒立的像的高度是，则蜡烛火焰的高度是______cm．
12. 如图，点A，B在反比例函数的图象上，点C，D在反比例函数的图象上，轴，已知点A，B的横坐标分别为2，4，与的面积之差为1，则k的值为______．

13. 如图，中，，，，D为内一动点，为的外接圆，交于点E，直线交于点P，，则的最小值为______．
三、解答题（共12小题，计81分）
14. 计算：；
15. 解不等式组：；
16. 解方程：．
17. 先化简，再求值：，其中．
18. 如图，在中，，，垂足为D．
（1）切线的性质：圆的切线 过切点的半径（填汉字）；
（2）尺规作图：求作，使得经过B，D两点，并与边相切于点C．（保留作图痕迹，不写作法）
19. 小明和小亮用如图所示的A、B两个转盘（每个转盘被分成三个面积相等的扇形）做游戏，转动两个转盘各一次，若两次数字之积超过6，则小明胜；若两次数字之积小于5，则小亮胜（若指针指向扇形的分界线，则需要重新转动），则这个游戏对双方公平吗?通过树状图或列表的方式说明理由．

20. 如图，菱形的对角线，交于点O，F是的中点，过点B作交的延长线于点E，连接，猜想四边形的形状，并进行证明．
21. 如图所示，实习期间小田接到任务测量塔的高度，但是无法直接测量．于是他先在塔附近的空地C处地面上水平放置了一个平面镜，然后他沿着方向移动，当移动到点E时，他刚好在平面镜内看到这座塔的顶端A的像，此时，测得顶端A的仰角为40°，米，小田同学眼睛与地面的距离米，已知点B，C，E在同一水平线上，且，均垂直于，若平面镜的厚度忽略不计，则这座塔的高度约为多少米．（参考数据：，，）（结果精确到0.1米）
22. 如图，矩形的四个顶点都在的边上，于点D，交于点N．
（1）求证：；
（2）若，，设的长度为x，矩形的面积为y，则矩形的面积是否有最大值？如果有，请求出矩形面积的最大值：如果没有，请说明理由．
23. 如图，在中，，平分交于点E，点D在上，，是的外接圆，交于点F．
（1）求证：是的切线；
（2）若的半径为4，，求的长．
24. 如图，抛物线：与x轴交于点和点，与y轴交于点C．
（1）求抛物线表达式及顶点D的坐标；
（2）如图1，点P为直线上方抛物线上一个动点，设点P的横坐标m．当m为何值时，的面积最大？并求出这个面积的最大值．
（3）在图2中，将抛物线关于x轴对称，得到新的抛物线：，新的抛物线与y轴交于点E，点M是y轴上一点，点N是平面内一点，是否存在点M，N，使以点B，E，M，N为顶点的四边形为菱形，若存在，请直接写出点N的坐标：若不存在，请说明理由．
25. 问题提出：
（1）如图1，在中，，，则当边上高为 时，的面积最大；
问题探究：
（2）如图2，在直角三角形中，，，，点D、E分别为、边上的动点，且，连接、，交于点P，
①求证：；
②求的度数及面积的最大值．
问题解决：
（3）如图3，为进一步落实“双减”，让学生在课间十分钟动起来，我校将在一片空地上建如图所示的四边形活动场地（即四边形）．其中，C、D分别为场地的入口和出口，米，，，且．已知建设成本为每平方米10元，求建设满足要求的场地，最多需要投入多少元？
x
…
0
1
2
…
y
…
5
0
…