

所属成套资源:河北省各地区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
河北省唐山市丰润区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
展开
这是一份河北省唐山市丰润区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共21页。试卷主要包含了选择题等内容,欢迎下载使用。
1. 下列图形中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000023米.用科学记数法表示0.000000023为( )
A. 23×10﹣10B. 2.3×10﹣10C. 2.3×10﹣9D. 2.3×10﹣8
4. 若,则2n-3m的值是( )
A. -1B. 1C. 2D. 3
5. 若M=(x-3)(x-4),N=(x-1)(x-6),则M与N的大小关系为()
A. M>NB. M=NC. M<ND. 由x的取值而定
6. 若一个正多边形的一个内角为,则这个图形为正( )边形
A. 八B. 九C. 七D. 十
7. 已知三角形的两边长分别为6,11,那么第三边的长可以是( )
A. 3B. 4C. 5D. 6
8. 如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为( )
A. 40°B. 50°C. 80°D. 100°
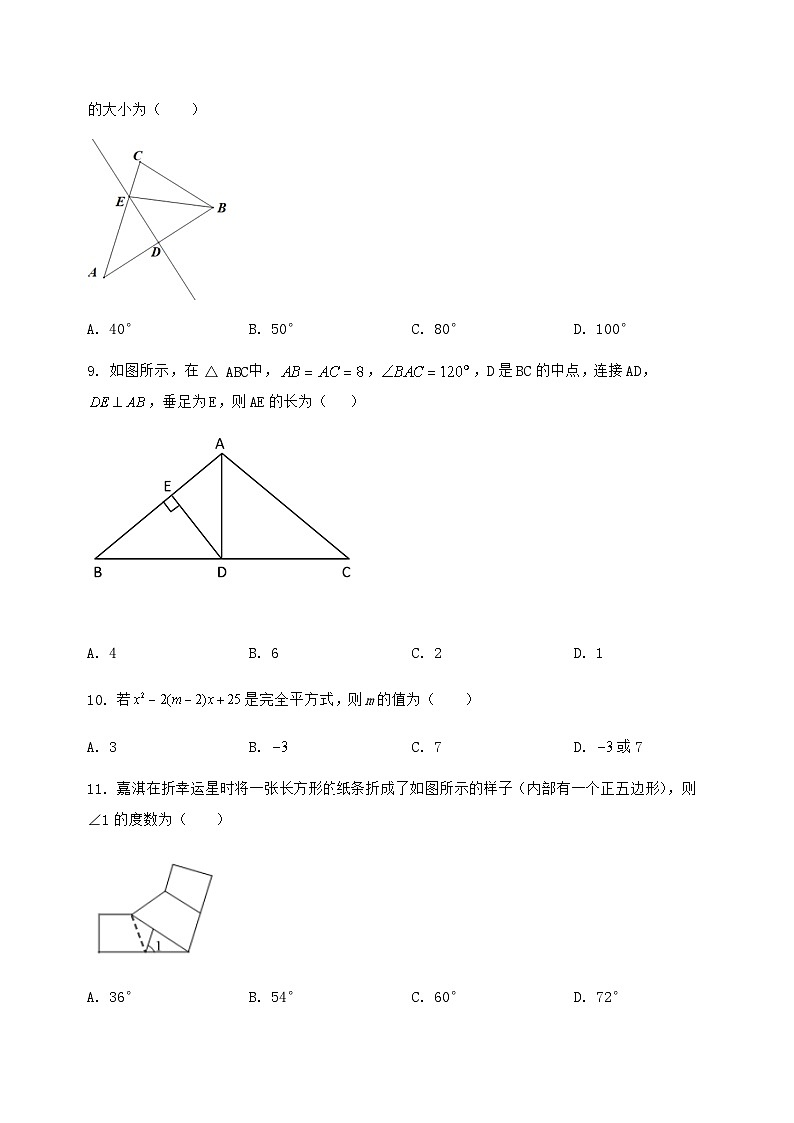
9. 如图所示,在△ABC中,,,D是BC的中点,连接AD,,垂足为E,则AE的长为( )
A. 4B. 6C. 2D. 1
10. 若是完全平方式,则m的值为( )
A. 3B. C. 7D. 或7
11. 嘉淇在折幸运星时将一张长方形纸条折成了如图所示的样子(内部有一个正五边形),则∠1的度数为( )
A. 36°B. 54°C. 60°D. 72°
12. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA 2,则PQ的长不可能是( )
A. 4B. 3.5
C. 2D. 1.5
13. 点在的角平分线上,点到边的距离等于,点是边上的任意一点,则下列选项正确的是( )
A. B. C. D.
14. 如图,在ΔABC中,DE是AC的垂直平分线,AE=3cm,ΔABD的周长为13cm,则ΔABC的周长是( )
A. 13cmB. 16cmC. 19cmD. 22cm
15. 如图,已知在△ABC中,,点D,E分别在边,上,,,若,则的度数为( )
A. 30°B. 40°C. 50°D. 60°
16. 北京大兴国际机场于2019年9月25日正式投入运营.小贝和小京分别从A地和B地出发赶往机场乘坐飞机,出行方式、路径及路程如下表所示:
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为x公里/时,根据题意可列方程( )
A. B.
C. D.
二.填空题(本大题共3题,总计 12分)
17. 请写出一个运算式子,使运算结果等于.你写的运算式子是______.
18. 有一三角形纸片ABC,∠A=70°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两个纸片均为等腰三角形,则∠C的度数可以是_____.
19. 图,在△ABC中,AB AC,D为BC的中点,有下列结论:①△ABD ≌ △ACD;②∠B∠C;③AD平分∠BAC;④AD⊥BC;⑤△ABC的对称轴是线段AD. 其中正确的结论有__________个.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)雯雯在计算时,解答过程如下:
雯雯的解答从第______步开始出错,请写出正确的解题过程.
21. 先化简,再求值:(2﹣a)(3+a)+(a﹣5)2,其中a=4.
22. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出△ABC关于轴对称的.
(2)写出点的坐标(直接写答案).
(3)的面积为___________
23. 已知在△ABC中,,,是△ABC的高,分别交,于点E,F.
(1)如图1,若,且,求的度数;
(2)如图2,若.
①求的度数;
②求证:.
24. 实践与探索
如图1,边长为的大正方形有一个边长为的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
(1)上述操作能验证的等式是__________;(请选择正确的一个)
A. B. C.
(2)请应用这个公式完成下列各题:
①已知,,则__________.
②计算:
25. 在学习“分式方程应用”时,张老师板书了如下的问题,小明和小亮两名同学都列出了对应的方程.
根据以上信息,解答下列问题:
(1)小明同学所列方程中x表示______,列方程所依据的等量关系是________________________________;小亮同学所列方程中y表示______,列方程所依据的等量关系是________________________________;
(2)请你在两个方程中任选一个,解答老师的例题.
26. 如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
唐山市丰润区2024-2025学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:B
【解析】:轴对称的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够相互重合,则称该图形为轴对称图形.
根据定义,B选项的图形符合题意.
故选B.
2.【答案】:D
【解析】:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D.
3.【答案】:D
【解析】:解:0.000000023=2.3×10﹣8.
故选:D.
4.【答案】:B
【解析】:解:∵,
∴,
∴,
∴.
故选:B
5.【答案】:A
【解析】:解: M=(x-3)(x-4)=
N=(x-1)(x-6)=
即:
故选:A.
6.【答案】:D
【解析】:解:设所求正n边形边数为n, 则
解得
故答案为:D.
7.【答案】:D
【解析】:设第三边长为x,由题意得:
11﹣6<x<11+6,
解得:5<x<17.
故选D.
8.【答案】:C
【解析】:∵线段AB的垂直平分线交AB于D,交AC于E,
∴AE=BE,
∴∠ABE=∠A=40°,
∵∠BEC=∠A+∠ABE
∴∠BEC=40°+40°=80°.
故选:C.
9.【答案】:C
【解析】:解: , ,D为BC中点,
,
,
,D为BC中点,
,
,
, ,
,
.
故答案为:C.
10.【答案】:D
【解析】:∵关于x的二次三项式是一个完全平方式,
∴m-2=±1×5,
∴m=7或-3,故D正确.
故选:D.
【画龙点睛】本题主要考查了完全平方公式的应用,解答此题的关键是要明确:.
11.【答案】:D
【解析】:∵折的图形为正五边形,
∴∠2= =108°,
又∵长方形纸片对边平行,
∴∠1+∠2=180°,
∠1=180°-∠2=180°-108°=72°
故选D.
12.【答案】:D
【解析】:解:当PQ⊥OM时,PQ的值最小,
∵OP平分∠MON,PA⊥ON,PA=2,
∴PQ=PA=2,
所以的最小值为2,
所以A,B,D不符合题意,D符合题意;
故选:D.
13.【答案】:B
【解析】:∵点P在∠AOB的平分线上,点P到OA边的距离等于5,
∴点P到OB的距离为5,
∵点Q是OB边上的任意一点,
∴PQ≥5.
故选:B.
14.【答案】:C
【解析】:解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故选:C.
15.【答案】:C
【解析】:如图,过点D作于点F.
∴在△DBE和中,
∴△DBE≅△DFC(AAS),
∴,
∴AD为的角平分线,
∴,
∴.
故选C.
16.【答案】:B
【解析】:解:设公交的平均速度为x公里/时,则地铁的平均速度为2x公里/时,
由题意得:,
故选B.
二. 填空题
17.【答案】: (答案不唯一)
【解析】:.
故答案为∶(答案不唯一).
【画龙点睛】本题考查了同底数幂相乘的法则,解题的关键是注意掌握同底数幂的运算法则.
18.【答案】: 20°或35°或27.5°
【解析】:由题意知△ABD与△DBC均为等腰三角形,
对于△ABD可能有①AB=BD,此时∠ADB=∠A=70°,
∴∠BDC=180°﹣∠ADB=180°﹣70°=110°,
∠C=(180°﹣110°)=35°,
②AB=AD,此时∠ADB=(180°﹣∠A)=(180°﹣70°)=55°,
∴∠BDC=180°﹣∠ADB=180°﹣55°=125°,
∠C=(180°﹣125°)=27.5°,
③AD=BD,此时,∠ADB=180°﹣2×70°=40°,
∴∠BDC=180°﹣∠ADB=180°﹣40°=140°,
∠C=(180°﹣140°)=20°,
综上所述,∠C度数可以为20°或35°或27.5°.
故答案为:20°或35°或27.5°
【画龙点睛】本题考查了等腰三角形的性质,难点在于分情况讨论.
19.【答案】: 4
【解析】:解:∵AB=AC,BD=CD,
∴∠B=∠C,∠BAD=∠CAD,AD⊥BC,
在△ABD和△ACD中
∴△ABD≌△ACD,
△ABC的对称轴是线段AD所在的直线.
∴①②③④都符合题意,⑤不符合题意;
故答案为4.
三.解答题
20【答案】:
(1);(2)一,见解析
【解析】:
(1)
;
(2)一,
m(1+m)−(m−1)2
=m+m2−(m2−2m+1)
=m+m2−m2+2m−1
=3m−1.
21【答案】:
﹣11a+31,-13.
【解析】:
解:(2﹣a)(3+a)+(a﹣5)2
=6+2a﹣3a﹣a2+a2﹣10a+25
=﹣11a+31,
当a=4时,原式=﹣11×4+31=﹣44+31=﹣13.
22【答案】:
(1)见解析;(2)A1(-1,2)、B1(-3,1)、C1(2,-1);(3)
【解析】:
解:(1)如图所示,△A1B1C1即为所求.
(2)由图知,A1(-1,2)、B1(-3,1)、C1(2,-1);
(3)△A1B1C1的面积=
23【答案】:
(1)30° (2)①;②见解析
【解析】:
【小问1详解】
∵BF⊥AC,
∴∠AFB=90°,
∵∠BAC=45°,
∴∠ABF=90°-∠BAC=45°,
∵∠BDE=75°,
∴∠BAE=∠BDE-∠ABF=30°;
【小问2详解】
①∵∠ABC=∠C,
∴AB=AC,
∵AE⊥BC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=22.5°;
②证明:∵∠BAC=45°,BF⊥AC,
∴∠AFB=90°,
∴∠ABF=∠BAC=45°,
∴FA=FB,
∵BF⊥AC,AE⊥BC,
∴∠CFB=∠AFD=∠AEC=90°,
∴∠C+∠CAE=90°,∠ADF+∠CAE=90°,
∴∠ADF=∠C,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(AAS).
24【答案】:
(1)A;(2)①4;②5050
【解析】:
(1)图1表示,图2的面积表示,两个图形阴影面积相等,得到
故选A ;
(2)①
∵
∴,解得
②原式=(1002-992)+(982-972)+…+(42-32)+(22-12)
=(100+99)(100-99)+(98+97)(98-97)+…+(4+3)(4-3)+(2+1)(2-1)
=100+99+98+97+…+4+3+2+1
=101×50
=5050
【画龙点睛】本题考查了平方差公式的几何证明,题目较为简单,需要利用正方形和长方形的面积进行变形求解.
25【答案】:
(1)甲队每天修路的米数;甲队修路800m与乙队修路1200m所用时间相等;甲队修路800m所用时间;乙队每天比甲队多修40m
(2)甲队每天修路为80m
【解析】:
【小问1详解】
x表示甲队每天修路的米数;
等量关系是:甲队修路800m与乙队修路1200m所用时间相等
y表示甲队修路800m所用时间;
等量关系是:乙队每天比甲队多修40m
【小问2详解】
解:若小明设甲队每天修xm,则:
解这个分式方程
经检验,是原分式方程的根
答:甲队每天修路为80m.
设甲队修路800m所用时间为y天,
,
解得:y=10,
经检验,是原分式方程的根,
(m),
答:甲队每天修路为80m.
26【答案】:
(1)见解析;(2)AP=2;(3)DE的长不变,定值为3.
【解析】:
(1)过P作PF∥QC交AB于F,则是等边三角形,根据AAS证明三角形全等即可;
(2)想办法证明BD=DF=AF即可解决问题;
(3)想办法证明即可解决问题.
【详解】(1)证明:过P作PF∥QC交AB于F,则是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在和中,
,
∴,
∴DQ=DP;
(2)解:∵,
∴BD=DF,
∵,
∴,
∴,
∴AP=2;
(3)解:由(2)知BD=DF,
∵是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF
=3,为定值,即DE的长不变.
【画龙点睛】本题主要考查了三角形全等的性质及判定,以及三角形中的动点问题,熟练掌握相关几何综合的解法是解决本题的关键.出行方式
路径
路程
地铁
A地→大兴机场
全程约43公里
公交
B地→大兴机场
全程约54公里
…………第一步
…………第二步
…………第三步
15.3分式方程
例:有甲乙两个工程队,甲队修路800m与乙队修路1200m所用时间相等,乙队每天比甲队多修40m,求甲队每天修路的长度
小明: 小亮:
相关试卷
这是一份河北省内丘县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共24页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省元氏县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共23页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省井陉县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共21页。试卷主要包含了选择题等内容,欢迎下载使用。









