

2024-2025学年江苏省南京市六校高一(上)12月联合调研数学试卷(解析版)
展开
这是一份2024-2025学年江苏省南京市六校高一(上)12月联合调研数学试卷(解析版),共14页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 函数的定义域为( )
A. B. C. D.
【答案】C
【解析】要是函数式子有意义,则需要,解之可得,
函数的定义域为.
故选:C.
2. 已知是第二象限的角,为其终边上的一点,且,则( )
A B. C. D.
【答案】A
【解析】依题意,,(为坐标原点),
则,所以.
故选:A.
3. 若扇形面积为,圆心角为,那么该扇形的弧长为( )
A. B. C. D.
【答案】C
【解析】由扇形的面积公式可得,解得,
所以弧长为.
故选:C.
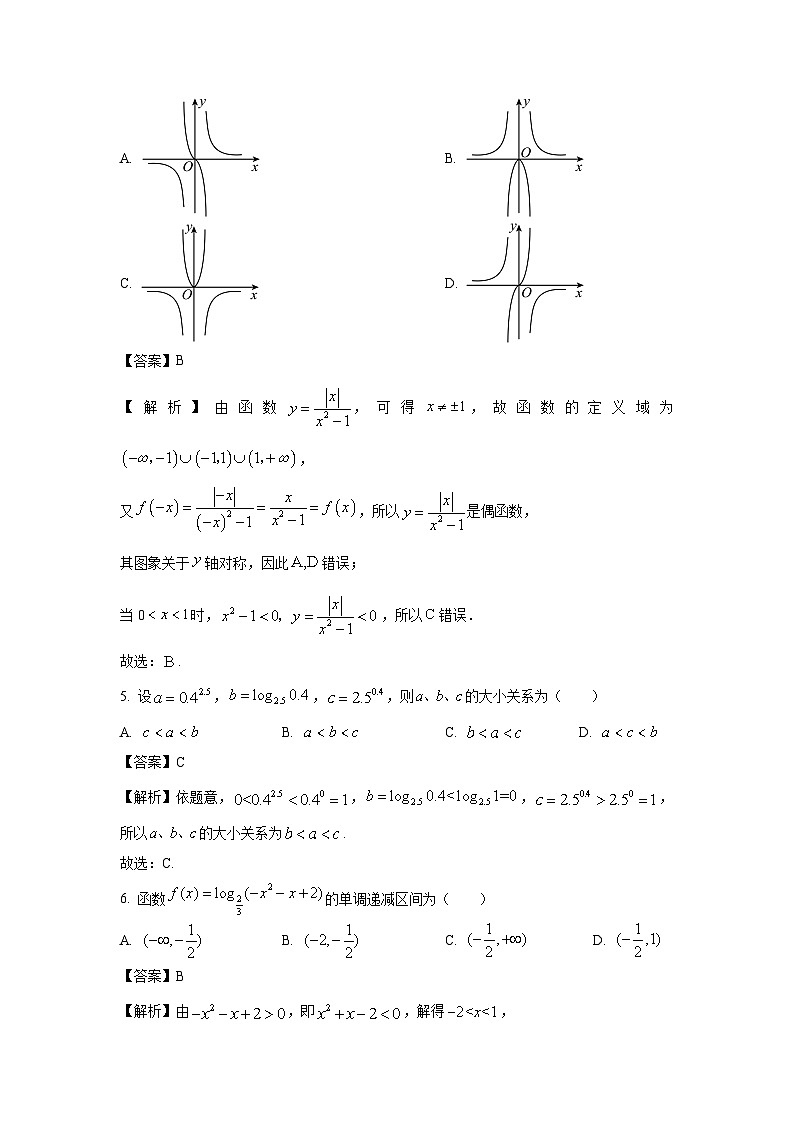
4. 函数 的图象大致为( )
A. B.
C. D.
【答案】B
【解析】由函数,可得,故函数的定义域为,
又,所以是偶函数,
其图象关于轴对称,因此错误;
当0时,,所以错误.
故选:.
5. 设,,,则的大小关系为( )
A. B. C. D.
【答案】C
【解析】依题意,,,,
所以的大小关系为.
故选:C.
6. 函数的单调递减区间为( )
A. B. C. D.
【答案】B
【解析】由,即,解得,
所以函数fx的定义域为,
令,则在上单调递增,在上单调递减,
因为为减函数,所以在上单调递减.
故选:B.
7. 已知函数,且,则的值为( )
A. B. C. D. 或1
【答案】B
【解析】当时,,解得(舍去)或,
此时;
当时,,解得,此时.
综上所述,.
故选:B.
8. 已知幂函数的图象关于轴对称,且在上单调递减,则满足的实数的取值范围为( )
A. B.
C. D.
【答案】C
【解析】因为函数在上单调递减,
所以,又,所以,
因为函数的图象关于轴对称,
所以为偶数,所以,
函数的定义域为,
且函数在和0,+∞上单调递减,
当时,,当时,,
所以不等式可化为或或,
所以或,所以的取值范围为.
故选:C.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对得部分分,有选错得0分.
9. 下列说法正确的有( )
A. 命题,则命题的否定是
B. 与不是同一个函数
C. 定义在上的函数为奇函数的充要条件是
D. “且”是“”的充分不必要条件
【答案】BD
【解析】A选项:命题,
则命题的否定是,A选项错误;
B选项:定义域:,定义域:,定义域不同,
与不是同一个函数,B选项正确;
C选项:定义在上的奇函数在0处函数值为0,但在0处函数值为0的函数不一定是奇函数;所以他们不是充要条件的关系,C选项错误;
D选项:当且时,成立,满足充分条件;
当时,且不成立,例如,,不满足必要条件;
所以“且”是“”的充分不必要条件,D选项正确.
故选:BD.
10. 若,,且,则下列说法正确的有( )
A. 的最小值是 B. 的最大值是
C. 的最小值是 D. 的最小值是
【答案】ACD
【解析】对A:因为,
即(当且仅当即时取“”),故A项正确;
对B:因为,
当且仅当即时取“”,故B项错误;
对C:因为,
所以1a2+4b2≥12(当且仅当即时取“”),故C项正确;
对D:由,所以,
由B知:成立,故D项正确.
故选:ACD.
11. 若定义在上不恒为的,对于都满足,且当时,,则下列说法正确的有( )
A. B. 为奇函数
C. D. 在上单调递减
【答案】ABD
【解析】对于A:令,则,所以,故正确;
对于B:令,则,所以,
且定义域为关于原点对称,所以为奇函数,故正确;
对于CD:,则,
因为,所以,所以,所以,
因为,
且,
所以,所以,即,
因为时,,所以,
所以,所以在上单调递减,故D正确;
又因为,且,所以,故C错误.
故选:ABD.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知,且,则角是第__________象限角.
【答案】三
【解析】因为,所以是第二象限角或者第三象限角,
或者终边在轴的非正半轴,
当时,则是第一象限角或者第三象限角,故是第三象限角.
13. 若函数,且的图象恒过定点,则______.
【答案】
【解析】因为函数的图象恒过定点,
所以,,所以,,
所以.
14. 已知函数,若关于的方程有4个不同的实根x1、、、,且,则的取值范围为______.
【答案】
【解析】作出函数y=fx和函数的图象如下图所示,
则两个函数的图象共有4个交点,且横坐标分别为x1、、、,
且,
,由,得,
则有,所以,
,化简得,,,
由于二次函数图象对称轴为直线,
则点两点关于直线对称,所以,且由图象可知,
所以,又,
由二次函数的性质可得,所以.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知集合,
(1)当时,求与;
(2)若,求实数的取值范围.
解:(1),
当时,,,
所以=,.
(2)因为,所以,
若,,满足题意,
若,,,
由,得,
综上:或.
16. 已知函数,若函数在区间上的最大值与最小值之和为.
(1)求函数解析式,并求出关于的不等式的解集;
(2)求函数,的值域,并求出取得最值时对应的的值.
解:(1)函数定义域为,且在上单调,
由函数在区间上的最大值与最小值之和为,
得,即,解得,
于是;
,
解,得或;
解,即,得或,
因此或,
所以不等式的解集或.
(2)由(1)知,
,
令,由,得,,
当时,,此时;当时,,此时,
所以函数的值域为,取最小值时,取最大值时.
17. 为了号召并鼓励学生利用课余时间阅读名著,学校决定制定一个课余时间阅读名著考核评分制度,建立一个每天得分(单位:分)与当天阅读时间(单位:分钟)的函数关系,要求如下:
(i)函数的部分图象接近图示;
(ii)每天阅读时间为分钟时,当天得分为分;
(iii)每天阅读时间为分钟时,当天得分为50分;
(iiii)每天最多得分不超过分.
现有以下三个函数模型供选择:
①;
②;
③.
(1)请你根据函数图像性质从中选择一个合适的函数模型,不需要说明理由;
(2)根据你对(1)的判断以及所给信息完善你的模型,给出函数的解析式;
(3)已知学校要求每天的得分不少于分,求每天至少阅读多少分钟?
解:(1)从题图看应选择先快后慢增长的函数模型,故选.
(2)将,代入解析式,得到,解得,,
即
令,可得,解得x=150,
所以函数的解析式为.
(3)由,即,
即,解得,
所以每天得分不少于分,至少需要阅读分钟.
18. 已知定义在上的函数是奇函数.
(1)求函数的解析式;
(2)判断的单调性,并用单调性定义证明;
(3)若存在,使得关于的不等式能成立,求实数的取值范围.
解:(1)∵是定义在上的奇函数,∴,∴,
此时,,
∴是奇函数,满足题意,∴.
(2)是上的减函数.
∵,且,
则,
∵,∴,,,∴,
即,∴是上的减函数.
(3)∵是上的奇函数,
∴不等式即为,
∵是上的减函数,∴在时能成立;
令,则,当且仅当时取等号,
故在时能成立,
所以,
令,∵在上均单调递增,
∴在上单调递增,∴,故.
19. 对于两个定义域相同的函数和,若存在实数m,n,使,则称函数是由“基函数和”生成的.
(1)若是由“基函数和”生成的,求的值;
(2)试利用“基函数和”生成一个函数,满足为偶函数,且.
①求函数解析式;
②已知,对于上的任意值,,记,求的最大值.(注:.)
解:(1)由已知,可得,
则,
则,解得,所以实数的值为.
(2)①设,
因为偶函数,所以,
由,可得,
整理可得,即,所以,
所以对任意恒成立,所以,
所以,
又因为,所以,所以,
故函数的解析式为.
②由①知.
在内任取,且,
则,
因为
,,
所以,,所以,
所以,即,
所以,即,
所以函数在上是增函数,同理可证,函数在上是减函数.
设,
则,
所以
,
当且仅当或时,有最大值,
故的最小值为.
相关试卷
这是一份2024~2025学年江苏省南京市六校高一(上)期中联合调研数学试卷(解析版),共12页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
这是一份江苏省南京市六校联合体2024-2025学年高三上学期10月联合调研数学试卷(Word版附答案),文件包含数学试题docx、数学答案pdf、2024-2025学年第一学期六校联合体学情调研测试答题卡pdf等3份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
这是一份江苏省南京市六校2024-2025学年高一上学期期中联合调研考试数学试卷(Word版附答案),共8页。试卷主要包含了单项选择题,选择题,填空题,解答题等内容,欢迎下载使用。










