数学八年级下册4.2 平行四边形课文ppt课件

这是一份数学八年级下册4.2 平行四边形课文ppt课件，文件包含快来认识我教学课件pptx、这是我呀第一课时快来认识我教案doc、学习单docx、新建DOC文档doc、谭苏菁MP3、刘柠依m4a等6份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
掌握平行四边形的性质，并应用平行四边形的性质解决问题。
初步感受图形之间的联系，体会平移、旋转、转化等数学思想，获得初步研究图形的经验，积累数学活动经验.
直观认识平行四边形，建立平行四边形的表象.
提高在生活中观察和探究数学现象的意识和能力。
观察下列图片，它们是什么几何图形的形象？
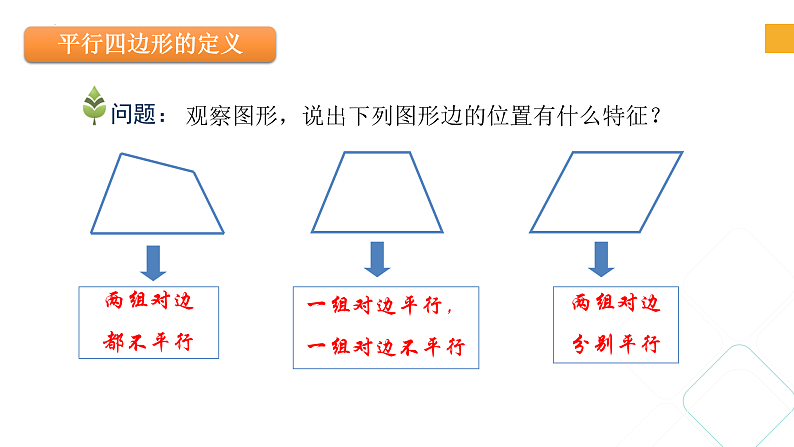
一组对边平行，一组对边不平行
观察图形，说出下列图形边的位置有什么特征？
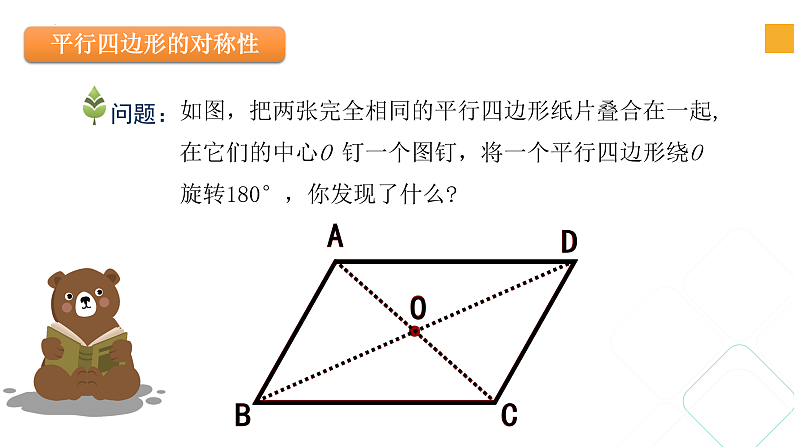
如图，把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉，将一个平行四边形绕O 旋转180°，你发现了什么?
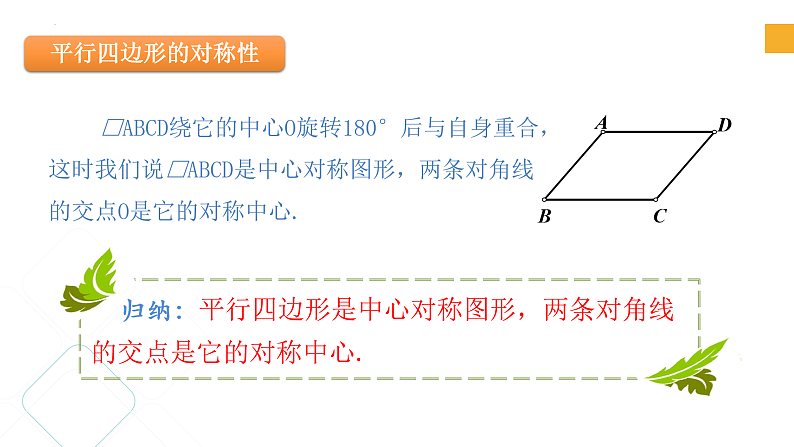
□ABCD绕它的中心O旋转180°后与自身重合，这时我们说□ABCD是中心对称图形，两条对角线的交点O是它的对称中心.
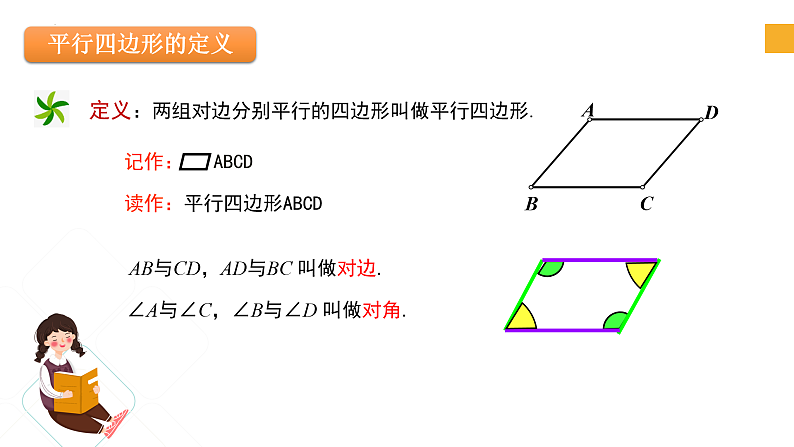
定义：两组对边分别平行的四边形叫做平行四边形.
AB与CD，AD与BC 叫做对边.
∠A与∠C，∠B与∠D 叫做对角.
记作： ABCD
读作：平行四边形ABCD
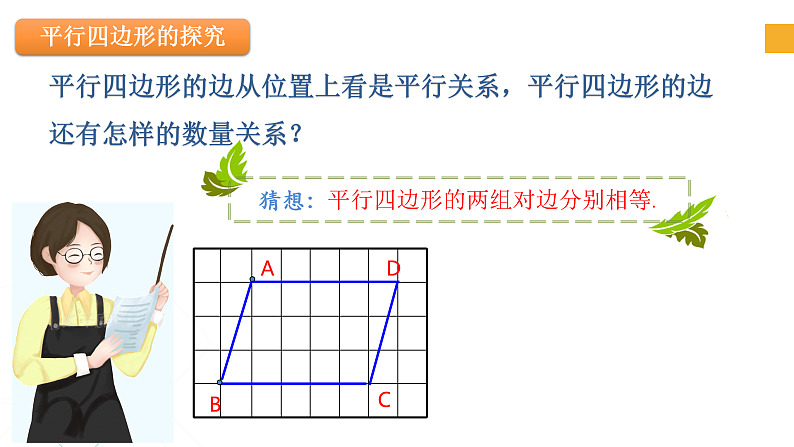
平行四边形的边从位置上看是平行关系，平行四边形的边还有怎样的数量关系？
∵四边形ABCD是平行四边形∴AB∥CD，AD∥BC
∴∠3＝∠4，∠1＝∠2
∠1＝∠2AC＝CA∠3＝∠4
∴ △ABC≌△CDA（ASA）
在△ABC和△CDA中
已知： ABCD求证：AB=CD，BC=DA
∴AB＝CD，BC＝DA.
归纳：平行四边形的性质：平行四边形对边平行，平行四边形对边相等.几何语言：∵四边形ABCD是平行四边形， ∴AB∥CD，AD∥BC，AB＝CD，AD＝BC.
探究过平行四边形边的关系，它的角之间有什么关系？
请同学们自己证明∠BAD =∠DCB.
归纳：平行四边形的性质：平行四边形的性质：平行四边形的两组对角分别相等，邻角互补.几何语言：∵四边形ABCD是平行四边形， ∴∠A＝∠C，∠B＝∠D， ∠A＋∠B＝180°，∠B＋∠C＝180°， ∠C＋∠D＝180°，∠A＋∠D＝180°.
如图，在□ABCD中，连接AC,BD,并设它们相交于点O. OA与OC,OB与OD有什么关系?你能证明发现的结论吗？
∴ AD=BC，AD∥BC,
∴ ∠1=∠2，∠3=∠4,
∴ △AOD≌△COB（ASA）,
∴ OA=OC，OB=OD.
∵四边形ABCD是平行四边形，
归纳：对角线的性质：平行四边形的对角线互相平分．几何语言：如图，∵四边形ABCD是平行四边形， 对角线AC，BD相交于点O， ∴OA＝OC，OB＝OD.
若a // b，作 AD // GH // BC，分别交 b于D、H、C，交 a于A、G、B.
则 GH=AD=BC.
则 DA= HG =CB.
（因为平行四边形的对边相等）
若a // b，DA、GH、CB垂直于 a，交a于A、G、B，交 b于D、H、C.
例 如图，平行四边形ABCD的对角线AC与BD相交于点O，过点O作直线与AD，BC分别相交于点E、F，求证：OE=OF.
∴ DO=BO，AD∥BC.
∴ ∠ODE=∠OBF.
∴ △DOE≌△BOF（ASA）.
∵ ∠DOE=∠BOF，
归纳：重要结论 1. △ABO≌ △CDO， △AOD ≌ △COB， △ ABD ≌ △CDB， △ ABC ≌ △CDA ；2. △ABO、 △AOD、 △DOC、 △COB的面积相等，且都等于平行四边形面积的四分之一.
Synergistically utilize technically sund prtals with, Synergistically utilize technically sund
例 已知：如图，在 ABCD中, E、F是对角线AC上的两点，并且AE=CF，求证： BE=DF.
证明：∵四边形ABCD是平行四边形，
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF（SAS）.
∴ AB=CD，AB ∥ CD
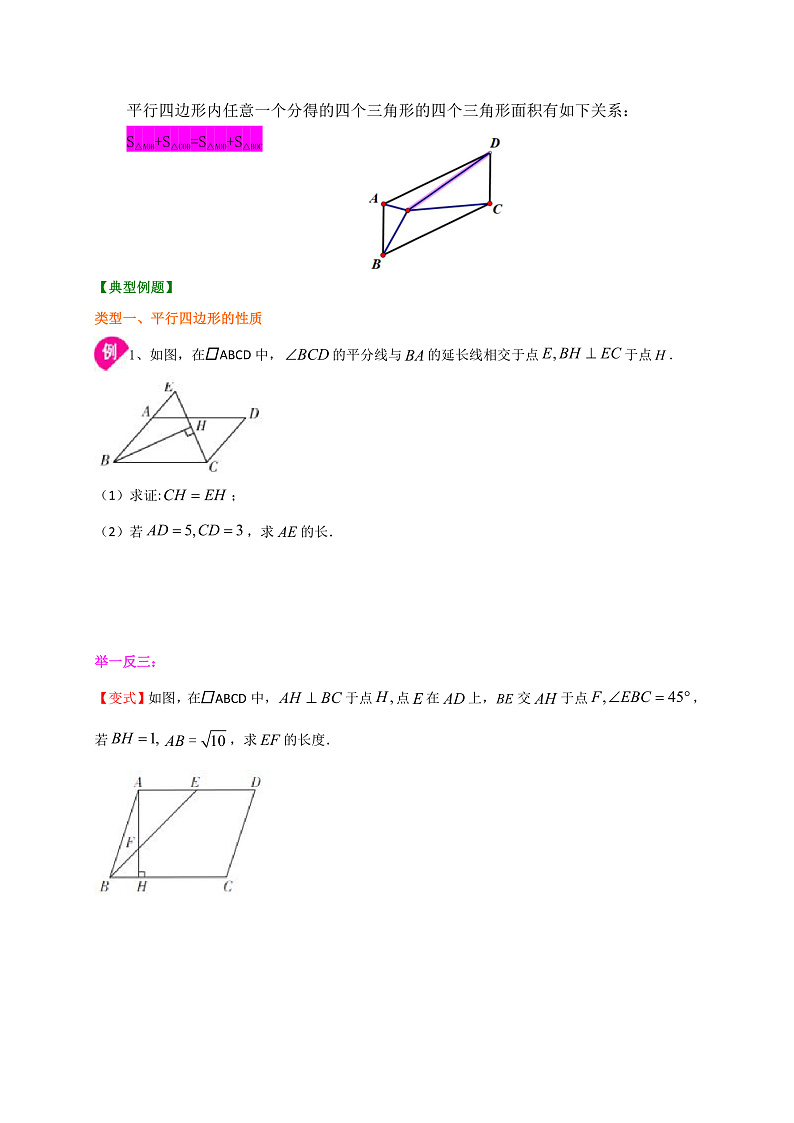
证明： ∵四边形ABCD是平行四边形， ∴ AB∥CD，AD=BC，∴ ∠CDE= ∠DEA，∠CFB= ∠FBA.又∵DE，BF分别平分∠ADC，∠ABC ，∴∠CDE= ∠ADE，∠CBF= ∠FBA，∴ ∠DEA= ∠ADE，∠CFB=∠CBF ，∴AE=AD ， CF=BC ，∴AE= CF.
如图，在平行四边形ABCD中，DE平分∠ADC,BF平分∠ABC.求证:AE=CF.
如图，AB∥CD，BC⊥AB，若AB=4cm，S△ABC = 12cm2，求△ABD 中 AB 边上的高．
解：S△ABC = AB•BC,= ×4 ×BC=12cm2，∴BC=6cm.∵AB∥CD，∴点 D 到 AB 边的距离等于BC的长度，∴△ABD 中 AB 边上的高为6cm．
学校买了四棵树，准备栽在花园里，已经栽了三棵(如图)，现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树应该栽在哪里?．
如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD，交BC于点E.若△CDE的周长为10，则平行四边形ABCD的周长是多少？
解：∵四边形ABCD是平行四边形，∴AB=CD，BC=AD，OB=OD.∵OE⊥BD，∴BE=DE.∵△CDE的周长为10，∴DE+CE+CD=BE+CE+CD=BC+CD=10，∴平行四边形ABCD的周长为2×(BC+CD)=20．