数学八年级下册5.2 菱形教课内容ppt课件

经历从现实生活中抽象出图形的过程，了解菱形的概念及其与平行四边形的关系.
体会菱形的轴对称性，经历利用折纸等活动探索菱形性质的过程，发展合情推理能力.
在证明性质和运用性质解决问题的过程中进一步发展学生的逻辑推理能力.
从数学活动中获得成功的体验，充满对学习的好奇心和求知欲.
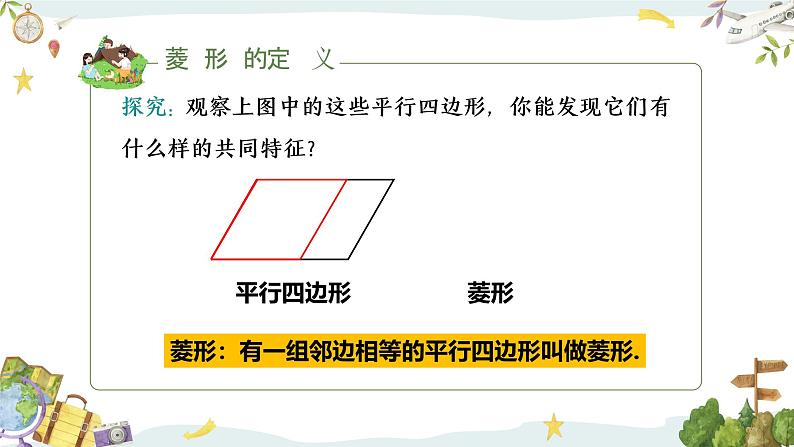
菱形：有一组邻边相等的平行四边形叫做菱形.
探究: 观察上图中的这些平行四边形，你能发现它们有什么样的共同特征？
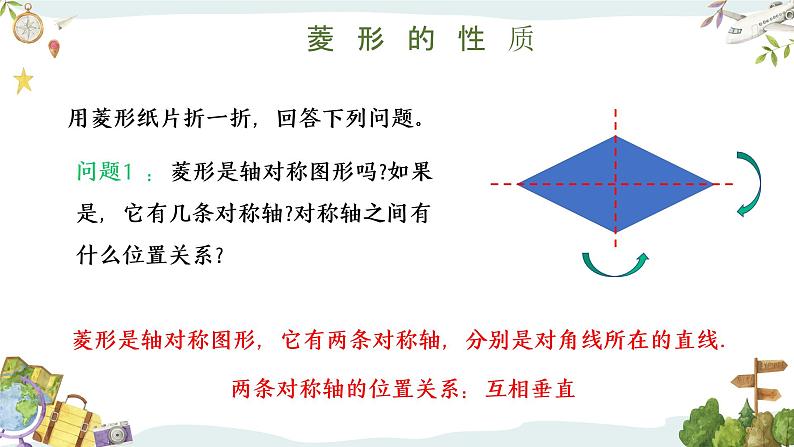
问题1 ：菱形是轴对称图形吗?如果是，它有几条对称轴?对称轴之间有什么位置关系?
菱形是轴对称图形，它有两条对称轴，分别是对角线所在的直线.
两条对称轴的位置关系：互相垂直
用菱形纸片折一折，回答下列问题。
问题2：菱形中有哪些相等的线段?
你能证明上面这些结论吗？
已知：如图，在平行四边形ABCD中，AB=AD，对角线AC与BD相交于点O. 求证:AB = BC = CD =AD；
证明：∵四边形ABCD是平行四边形， ∴AB = CD，AD = BC（平行四边形的对边相等）. 又∵AB=AD, ∴AB = BC = CD =AD.
已知：如图，在平行四边形ABCD中，AB=AD，对角线AC与BD相交于点O. 求证:AC⊥BD；
证明：∵AB = AD, ∴△ABD是等腰三角形. 又∵四边形ABCD是菱形, ∴OB = OD （菱形的对角线互相平分）.
在等腰三角形ABD中,∵OB = OD，∴AO⊥BD，即AC⊥BD
已知：如图，在平行四边形ABCD中，AB=AD，对角线AC与BD相交于点O. 求证:AC平分∠BAD,DB平分∠ADC；
在等腰三角形ABD中,∵OB = OD，∴AC平分∠BAD同理DB平分∠ADC
与平行四边形相同的性质
对角线互相垂直对角线平分对角
如图，菱形花坛ABCD的边长为20 m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长和花坛的面积.
S菱形ABCD = 底 × 高
菱形的面积等于它的两条对角线长的积的一半.
例 如图，E，F分别是菱形ABCD的边AB，AD的中点，且AB=5，AC=6.△OEF是什么三角形？证明你的结论.
证明△BOE ≌ △DOF
证明△AOE ≌ △AOF
证明∠OEF=∠OFE
E，F分别是边AB，AD的中点
1. 如图，在等腰△ABC中，AB=BC，BO⊥AC于点O，点D是BO上一点，延长BO至点E，使OE=OD．(1)求证：四边形是菱形；(2)若四边形的周长为20，两条对角线与的和等于14， 求四边形的面积．
（1）∵AB=BC，BO⊥AC， ∴AO=CO， 又∵OE=OD， ∴四边形ADCE是平行四边形， ∵DE⊥AC， ∴平行四边形ADCE是菱形；
一张四边形纸板ABCD形状如图，它的两条对角线相等.若要从这张纸中剪出一个菱形，并使它的四个顶点分别落在四边形ABCD的四条边上，可怎样剪？
解：如图，在AB、BC、CD、AD上取中点E、F、G、H，连接EF、FG、GH、HE,
∴EF∥HG，EF=HG∴四边形EFGH是平行四边形∵AC=BD∴HE=EF
∴四边形EFGH是菱形.