





所属成套资源:2025年高考数学一轮复习课件
56 第7章 第4课时 空间直线、平面的平行-2025年高考数学一轮复习课件
展开
这是一份56 第7章 第4课时 空间直线、平面的平行-2025年高考数学一轮复习课件,共30页。PPT课件主要包含了链接教材夯基固本,典例精研核心考点等内容,欢迎下载使用。
第4课时 空间直线、平面的平行
从定义和基本事实出发,借助长方体,通过直观感知,了解空间中直线与直线、直线与平面、平面与平面的平行关系,并加以证明.
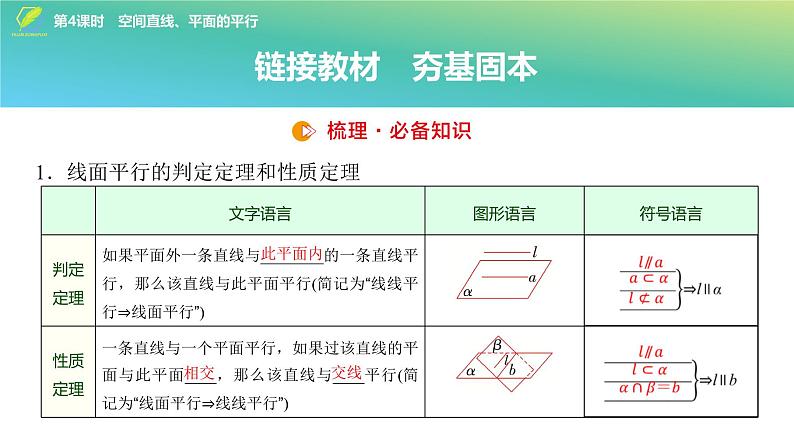
1.线面平行的判定定理和性质定理
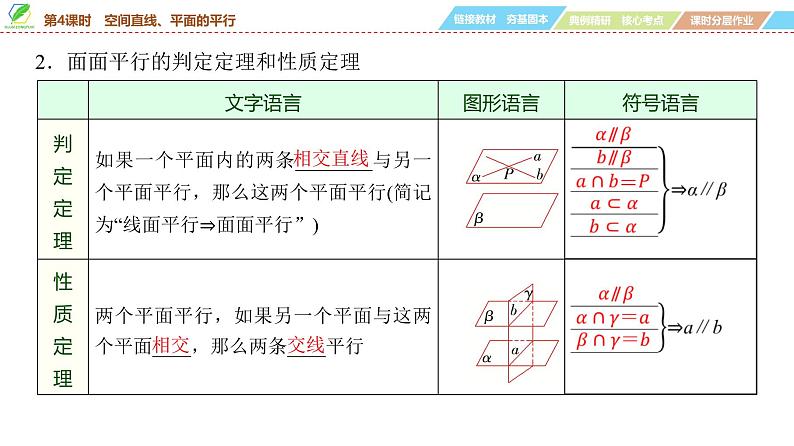
2.面面平行的判定定理和性质定理
[常用结论]1.平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β ,则α∥β.(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.(3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.2.与平行关系有关的性质(1)夹在两个平行平面之间的平行线段长度相等.(2)两条直线被三个平行平面所截,截得的对应线段成比例.(3)同一条直线与两个平行平面所成的角相等.
一、易错易混辨析(正确的打“√”,错误的打“×”)(1)若一条直线平行于一个平面,则这条直线平行于这个平面内的任一条直线.( )(2)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( )(3)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( )(4)若直线a与平面α内无数条直线平行,则a∥α.( )
二、教材经典衍生1.(人教A版必修第二册P142练习T2改编)平面α∥平面β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥αD [若α∩β=l,a∥l,a⊄α,a⊄β,a∥α,a∥β,排除A.若α∩β=l,a⊂α,a∥l,则a∥β,排除B.若α∩β=l,a⊂α,a∥l,b⊂β,b∥l,则a∥β,b∥α,排除C.故选D.]
2.(人教A版必修第二册P139练习T3改编)下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥αD [A错误,a可能在经过b的平面内;B错误,a与α内的直线平行或异面;C错误,两个平面可能相交.]3.(人教A版必修第二册P170复习参考题8T7改编)如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为______________.平行四边形 [∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.]
4.(人教A版必修第二册P134例1改编)如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则(1)当AC,BD满足条件____________时,四边形EFGH为菱形;(2)当AC,BD满足条件_____________________时,四边形EFGH为正方形.
AC=BD且AC⊥BD
考点一 直线与平面平行的判定与性质考向1 直线与平面平行的判定[典例1] 如图,P是平行四边形ABCD所在平面外的一点,E,F分别为AB,PD的中点,求证:AF∥平面PCE. [四字解题]
法二(应用面面平行的性质定理):如图,设G为CD的中点,连接FG,AG.∵F,G分别为PD,CD的中点,∴FG∥PC.又E为AB中点,四边形ABCD为平行四边形,∴AE綉GC,∴四边形AECG为平行四边形,AG∥EC,又FG⊄平面PCE,AG⊄平面PCE.PC⊂平面PCE,EC⊂平面PCE,∴FG∥平面PCE,AG∥平面PCE.又FG,AG⊂平面AFG,FG∩AG=G,∴平面AFG∥平面PCE.又AF⊂平面AFG,∴AF∥平面PCE.
考向2 线面平行性质定理的应用[典例2] 如图,在直四棱柱ABCD-A1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1∩平面BB1D=FG.证明:FG∥平面AA1B1B.[证明] 在直四棱柱ABCD-A1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D.又CC1⊂平面CEC1,平面CEC1∩平面BB1D=FG,所以CC1∥FG.因为BB1∥CC1,所以BB1∥FG.而BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.
名师点评 判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点).(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).(3)利用面面平行的性质(α∥β,a⊂α⇒a∥β).(4)利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).提醒:应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面确定交线.
[跟进训练]1.如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)若平面ADM∩平面BDE=l,平面ABM∩平面BDE=m,试分析l与m的位置关系,并证明你的结论.
[解] (1)证明:如图,记AC与BD的交点为O,连接OE.因为O,M分别为AC,EF的中点,四边形ACEF是矩形,所以四边形AOEM是平行四边形,所以AM∥OE.又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE.又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m∥AM,所以l∥m.
考点二 平面与平面平行的判定与性质[典例3] 如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.[证明] (1)∵G,H分别是A1B1,A1C1的中点,∴GH是△A1B1C1的中位线,GH∥B1C1.又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)∵在△ABC中,E,F分别为AB,AC的中点,∴EF∥BC.∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.∵A1G綉EB,∴四边形A1EBG是平行四边形,则A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.∵A1E∩EF=E,∴平面EFA1∥平面BCHG.
2.在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.
[证明] 如图所示,连接A1C交AC1于点M,∵四边形A1ACC1是平行四边形,∴M是A1C的中点,连接MD,∵D为BC的中点,∴A1B∥DM.∵A1B⊂平面A1BD1,DM⊄平面A1BD1,∴DM∥平面A1BD1.又由三棱柱的性质知,D1C1綉BD,∴四边形BDC1D1为平行四边形,∴DC1∥BD1.又DC1⊄平面A1BD1,BD1⊂平面A1BD1,∴DC1∥平面A1BD1.又∵DC1∩DM=D,DC1,DM⊂平面AC1D,∴平面A1BD1∥平面AC1D.
名师点评 证明面面平行的常用方法(1)利用面面平行的定义.(2)利用面面平行的判定定理.(3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”.(5)利用“线线平行”“线面平行”“面面平行”的相互转化.提醒:利用面面平行的判定定理证明两平面平行,需要说明在一个平面内的两条直线是相交直线.
[跟进训练]2.如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形.(1)证明:平面A1BD∥平面CD1B1;(2)若平面ABCD∩平面B1D1C=l,证明:B1D1∥l.
[证明] (1)由题设知BB1綉DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊄平面CD1B1,B1D1⊂平面CD1B1,所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC,所以四边形A1BCD1是平行四边形,所以A1B∥D1C.又A1B⊄平面CD1B1,D1C⊂平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,BD,A1B⊂平面A1BD,所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面B1D1C=l,平面ABCD∩平面A1BD=BD,所以l∥BD,在四棱柱ABCD-A1B1C1D1中,四边形BDD1B1为平行四边形,所以B1D1∥BD,所以B1D1∥l.
【教师备选资源】如图,在三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,A1B1,AB的中点.(1)求证:平面A1C1G∥平面BEF;(2)若平面A1C1G∩BC=H,求证:H为BC的中点.
[证明] (1)∵E,F分别为B1C1,A1B1的中点,∴EF∥A1C1,∵A1C1⊂平面A1C1G,EF⊄平面A1C1G,∴EF∥平面A1C1G,又F,G分别为A1B1,AB的中点,∴A1F=BG,又A1F∥BG,∴四边形A1GBF为平行四边形,则BF∥A1G,∵A1G⊂平面A1C1G,BF⊄平面A1C1G,∴BF∥平面A1C1G,又EF∩BF=F,EF,BF⊂平面BEF,∴平面A1C1G∥平面BEF.
(2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,由题意得平面A1C1G∩BC=H,即平面A1C1G∩平面ABC=GH,∴A1C1∥GH,得GH∥AC,∵G为AB的中点,∴H为BC的中点.
[解] (1)证明:∵在四棱锥P-ABCD中,底面ABCD是平行四边形,M,N,Q分别为BC,PA,PB的中点,∴NQ∥CD,MQ∥PC.∵NQ∩MQ=Q,CD∩PC=C,且NQ,MQ⊂平面MNQ,CD,PC⊂平面PCD,∴平面MNQ∥平面PCD.
名师点评 三种平行关系的转化线线平行 线面平行 面面平行提醒:解答探索性问题的基本策略是先假设,再证明.
[跟进训练]3.如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.(1)求证:CE∥平面PAD;(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论,若不存在,请说明理由.
巩固课堂所学 · 激发学习思维夯实基础知识 · 熟悉命题方式自我检测提能 · 及时矫正不足
本节课掌握了哪些考点?本节课还有什么疑问点?
课时分层作业(四十四)
相关课件
这是一份新高考数学一轮复习课件 第7章 §7.4 空间直线、平面的平行(含详解),共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,a⊄α,b⊂α,a∥b,a∥α,a⊂β,α∩β=b,此平面等内容,欢迎下载使用。
这是一份2025高考数学一轮复习-7.3空间直线、平面的平行【课件】,共58页。PPT课件主要包含了知识诊断基础夯实,直线与平面平行,一条直线,平面与平面平行,相交直线,平行四边形,考点突破题型剖析,又PM∥AB∥QN,分层训练巩固提升,①或③等内容,欢迎下载使用。
这是一份备战2024年高考总复习一轮(数学)第8章 立体几何 第4节 空间直线、平面的平行关系课件PPT,共40页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,平面外一条直线,过这条直线,相交直线等内容,欢迎下载使用。








