中考数学二轮复习模型解读与提分精练专题10 最值模型-胡不归问题（2份，原卷版+解析版）

这是一份中考数学二轮复习模型解读与提分精练专题10 最值模型-胡不归问题（2份，原卷版+解析版），文件包含中考数学二轮复习模型解读与提分精练专题10最值模型-胡不归问题原卷版doc、中考数学二轮复习模型解读与提分精练专题10最值模型-胡不归问题解析版doc等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
在解决胡不归问题主要依据是：①两点之间，线段最短；②垂线段最短。
【模型背景】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？
看到这里很多人都会有一个疑问，少年究竟能不能提前到家呢？假设可以提早到家，那么他该选择怎样的一条路线呢？这就是今天要讲的“胡不归”问题.
【模型解读】一动点P在直线MN外的运动速度为V1，在直线MN上运动的速度为V2，且V11，则提取系数，转化为小于1的形式解决即可）。
【最值原理】两点之间线段最短及垂线段最短。
例1．（2022·内蒙古·中考真题）如图，在△ABC中，AB＝AC＝4，∠CAB＝30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC．则PA+2PB的最小值为 _____．
例2．（2022·湖北武汉·一模）如图，在中，，，半径为的经过点，是圆的切线，且圆的直径在线段上，设点是线段上任意一点不含端点，则的最小值为______．
例3．（2021·眉山市·中考真题）如图，在菱形中，，对角线、相交于点，点在线段上，且，点为线段上的一个动点，则的最小值是______．
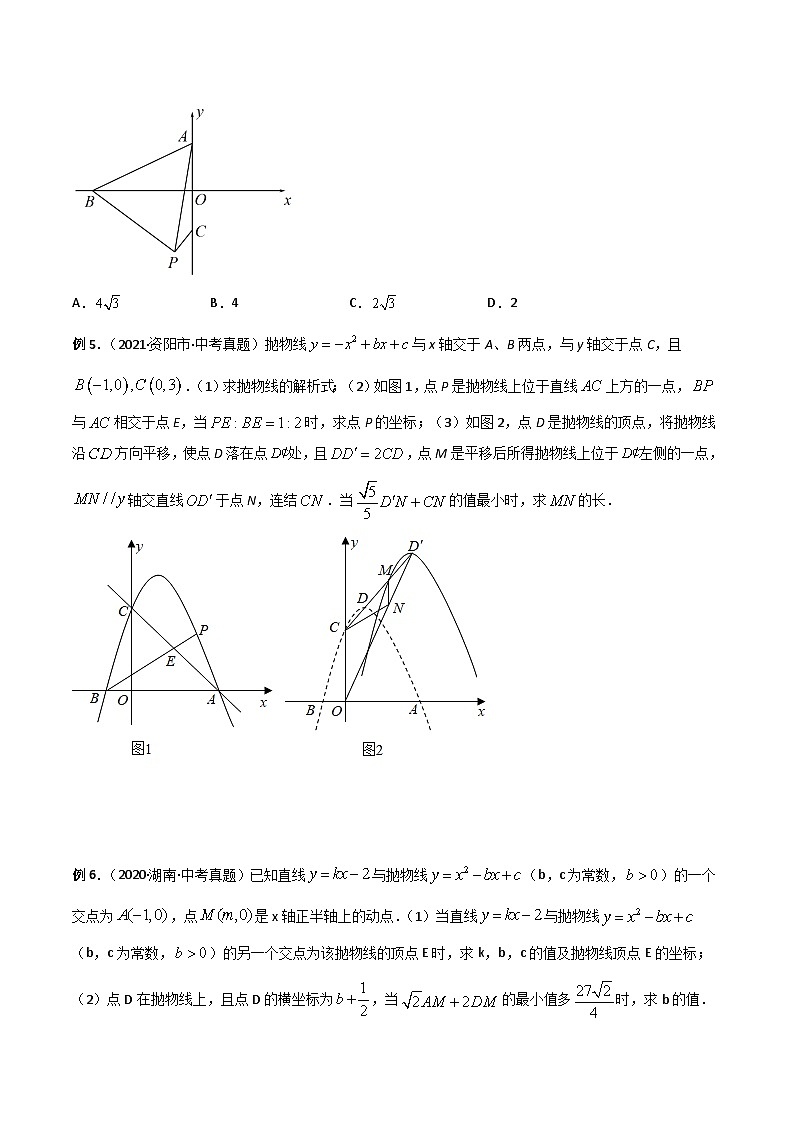
例4．（2022·山东淄博·二模）如图，在平面直角坐标系中，点A的坐标是，点C的坐标是，点是x轴上的动点，点B在x轴上移动时，始终保持是等边三角形（点P不在第二象限），连接，求得的最小值为（ ）
A．B．4C．D．2
例5．（2021·资阳市·中考真题）抛物线与x轴交于A、B两点，与y轴交于点C，且．（1）求抛物线的解析式；（2）如图1，点P是抛物线上位于直线上方的一点，与相交于点E，当时，求点P的坐标；（3）如图2，点D是抛物线的顶点，将抛物线沿方向平移，使点D落在点处，且，点M是平移后所得抛物线上位于左侧的一点，轴交直线于点N，连结．当的值最小时，求的长．
例6．（2020·湖南·中考真题）已知直线与抛物线（b，c为常数，）的一个交点为，点是x轴正半轴上的动点．（1）当直线与抛物线（b，c为常数，）的另一个交点为该抛物线的顶点E时，求k，b，c的值及抛物线顶点E的坐标；
（2）点D在抛物线上，且点D的横坐标为，当的最小值多时，求b的值．
例7．（2022·四川成都·中考模拟）6．如图，已知抛物线为常数，且与轴从左至右依次交于，两点，与轴交于点，经过点的直线与抛物线的另一交点为．
（1）若点的横坐标为，求抛物线的函数表达式；（2）若在第一象限内的抛物线上有点，使得以，，为顶点的三角形与相似，求的值；（3）在（1）的条件下，设为线段上一点（不含端点），连接，一动点从点出发，沿线段以每秒1个单位的速度运动到，再沿线段以每秒2个单位的速度运动到后停止，当点的坐标是多少时，点在整个运动过程中用时最少？
课后专项训练
1．（2022·河北·九年级期中）如图，在△ABC中，∠A＝15°，AB＝2，P为AC边上的一个动点（不与A、C重合），连接BP，则AP+PB的最小值是（ ）
A．B．C．D．2
2．（2022·江苏·九年级月考）如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AB＝4，点D、F分别是边AB，BC上的动点，连接CD，过点A作AE⊥CD交BC于点E，垂足为G，连接GF，则GF+FB的最小值是（ ）
A． B． C．D．
3．（2022·山东·九年级月考）如图，在平面直角坐标系中，二次函数y＝x2﹣2x＋c的图象与x轴交于A、C两点，与y轴交于点B（0，﹣3），若P是x轴上一动点，点D（0，1）在y轴上，连接PD，则PD＋PC的最小值是（ ）
A．4B．2＋2C．2D．
4．（2022·重庆·九年级期中）如图所示，菱形的边长为5，对角线的长为，为上一动点，则的最小值为
A．4B．5C．D．
5．（2022·浙江宁波·九年级开学考试）如图，在平面直角坐标系中，一次函数分别交x轴、y轴于A、B两点，若C为x轴上的一动点，则2BC+AC的最小值为__________．
6．（2022·湖南·九年级月考）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AB＝6，△BCD为等边三角形点E为△BCD围成的区域（包括各边）的一点过点E作EM∥AB，交直线AC于点M作EN∥AC交直线AB于点N，则AN+AM的最大值为 ．
7．（2022·湖北武汉·九年级期末）如图，▱中，，，为边上一点，则的最小值为______．
8．（2022·成都市七中育才九年级期中）如图，在平面直角坐标系中，直线l分别交x、y轴于B、C两点，点A、C的坐标分别为(3，0)、(0，﹣3)，且∠OCB＝60°，点P是直线l上一动点，连接AP，则的最小值是______．
9．（2022·四川自贡·一模）如图，中，，，于点，是线段上的一个动点，则的最小值是__________．
10．（2022·广东·一模）已知抛物线与x轴交于A，B两点（A在B点左侧），与y轴正半轴交于点C，点P是直线BC上的动点，点Q是线段OC上的动点．
(1)求直线BC解析式．(2)如图①，求OP＋PA的和取最小值时点P的坐标．
(3)如图②，求AQ＋QP的最小值．(4)如图③，求AQQC的最小值．
11．（2022·江苏·中考模拟）如图，抛物线与直线交于，两点，交轴于，两点，连接，，已知，．（Ⅰ）求抛物线的解析式和的值；（Ⅱ）在（Ⅰ）条件下：（1）为轴右侧抛物线上一动点，连接，过点作交轴于点，问：是否存在点使得以，，为顶点的三角形与相似？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．（2）设为线段上一点（不含端点），连接，一动点从点出发，沿线段以每秒一个单位速度运动到点，再沿线段以每秒个单位的速度运动到后停止，当点的坐标是多少时，点在整个运动中用时最少？
12．（2020·四川乐山市·中考真题）已知抛物线与轴交于，两点，为抛物线的顶点，抛物线的对称轴交轴于点，连结，且，如图所示．（1）求抛物线的解析式；（2）设是抛物线的对称轴上的一个动点．①过点作轴的平行线交线段于点，过点作交抛物线于点，连结、，求的面积的最大值；②连结，求的最小值．
13．（2021·四川达州市·中考真题）如图，在平面直角坐标系中，抛物线交轴于点和，交轴于点，抛物线的对称轴交轴于点，交抛物线于点．
（1）求抛物线的解析式；（2）将线段绕着点沿顺时针方向旋转得到线段，旋转角为，连接，，求的最小值．（3）为平面直角坐标系中一点，在抛物线上是否存在一点，使得以，，，为顶点的四边形为矩形？若存在，请直接写出点的横坐标；若不存在，请说明理由；
14．（2022·广西·南宁三中一模）如图，二次函数的图象交轴于点、，交轴于点，点是第四象限内抛物线上的动点，过点作轴交轴于点，线段的延长线交于点，连接、交于点，连接．（1）求二次函数的表达式；（2）当时，求点的坐标及；（3）在（2）的条件下，点是轴上一个动点，求的最小值．
15．（2022·广东·东莞市三模）已知，如图，二次函数图像交轴于，交交轴于点，是抛物线的顶点，对称轴经过轴上的点．（1）求二次函数关系式；（2）对称轴与交于点，点为对称轴上一动点．①求的最小值及取得最小值时点的坐标；
②在①的条件下，把沿着轴向右平移个单位长度时，设与重叠部分面积记为，求与之间的函数表达式，并求出的最大值．

16．（2022·天津·中考模拟）如图，在△ACE中，CA＝CE，∠CAE＝30°，⊙O经过点C，且圆的直径AB在线段AE上．（1）证明：CE是⊙O的切线；（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD＋OD的最小值为6时，求⊙O的直径AB的长．