

中考数学二轮复习几何模拟专项讲练模型42 相似形——一线三等角模型(2份,原卷版+解析版)
展开
这是一份中考数学二轮复习几何模拟专项讲练模型42 相似形——一线三等角模型(2份,原卷版+解析版),文件包含中考数学二轮复习几何模拟专项讲练模型42相似形一线三等角模型-原卷版doc、中考数学二轮复习几何模拟专项讲练模型42相似形一线三等角模型-解析版doc等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
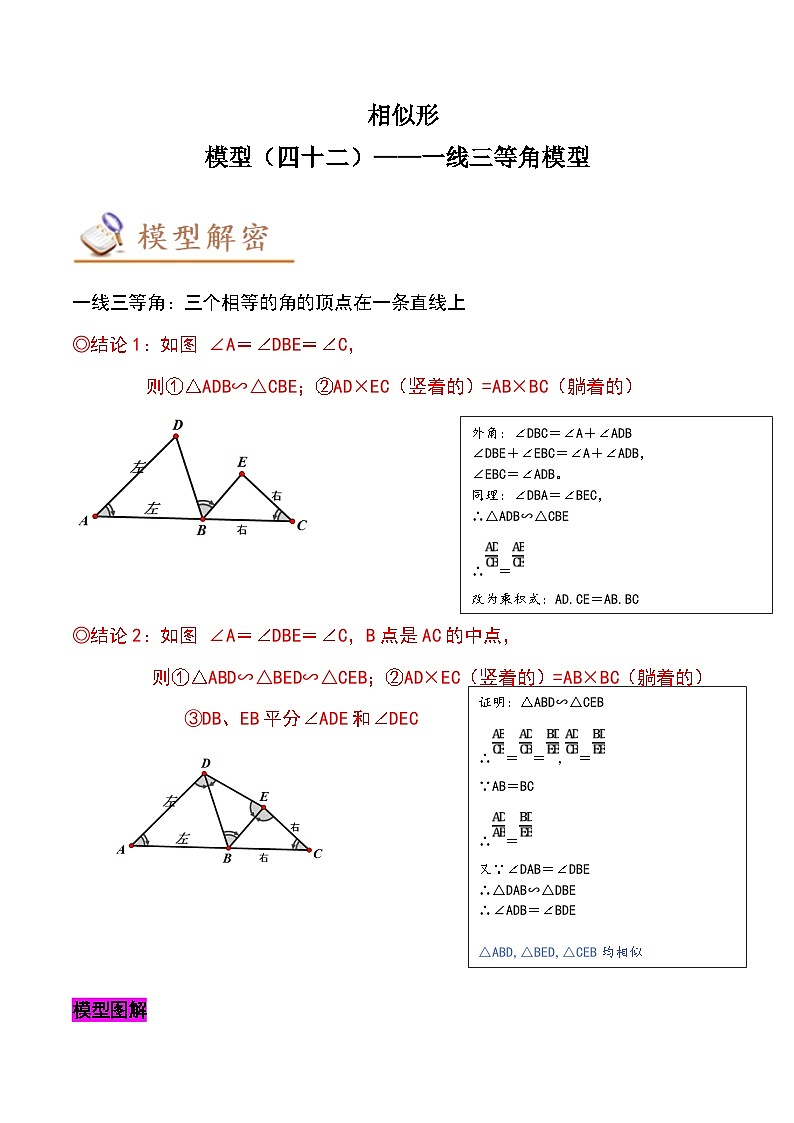
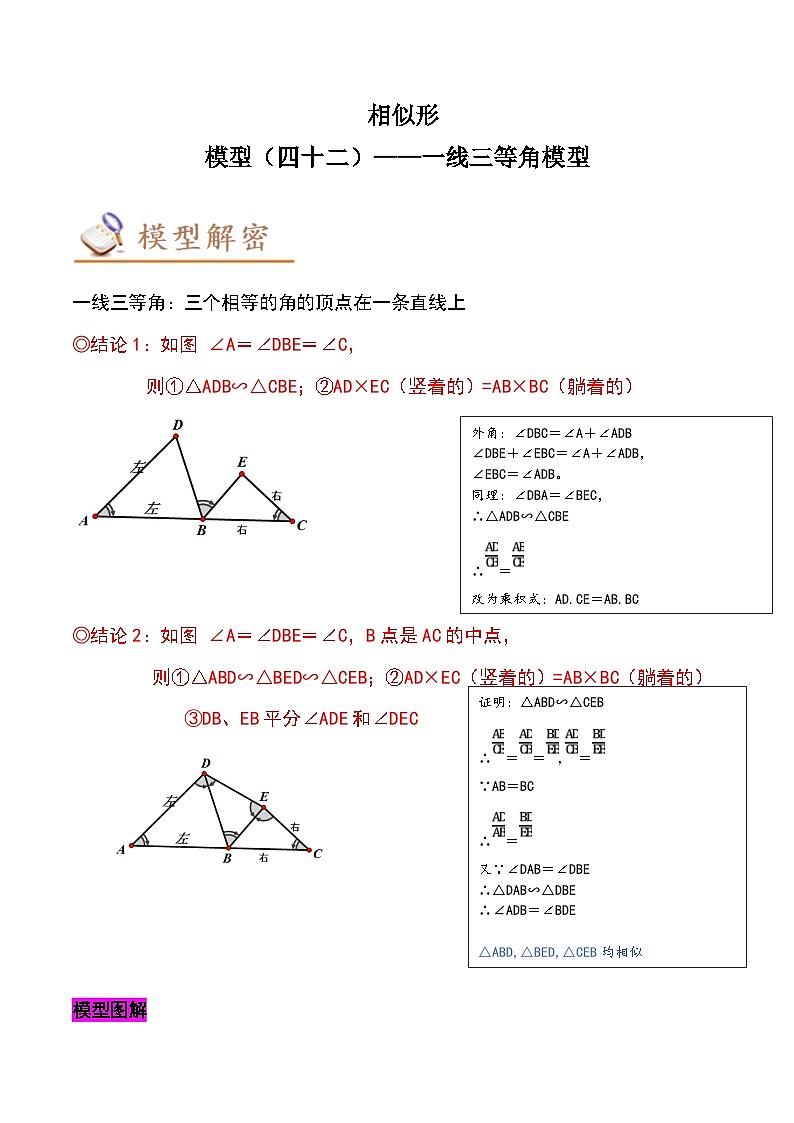
一线三等角:三个相等的角的顶点在一条直线上
◎结论1:如图 ∠A=∠DBE=∠C,
则①△ADB∽△CBE;②AD×EC(竖着的)=AB×BC(躺着的)
外角:∠DBC=∠A+∠ADB
∠DBE+∠EBC=∠A+∠ADB,
∠EBC=∠ADB。
同理:∠DBA=∠BEC,
∴△ADB∽△CBE
∴=
改为乘积式:AD.CE=AB.BC
一线三等角经典结论:左乘右=左乘右
◎结论2:如图 ∠A=∠DBE=∠C,B点是AC的中点,
证明:△ABD∽△CEB
∴==,=
∵AB=BC
∴=
又∵∠DAB=∠DBE
∴△DAB∽△DBE
∴∠ADB=∠BDE
△ABD,△BED,△CEB均相似
BD,BE为∠ADE,∠DEC角平分线
则①△ABD∽△BED∽△CEB;②AD×EC(竖着的)=AB×BC(躺着的)
③DB、EB平分∠ADE和∠DEC
模型图解
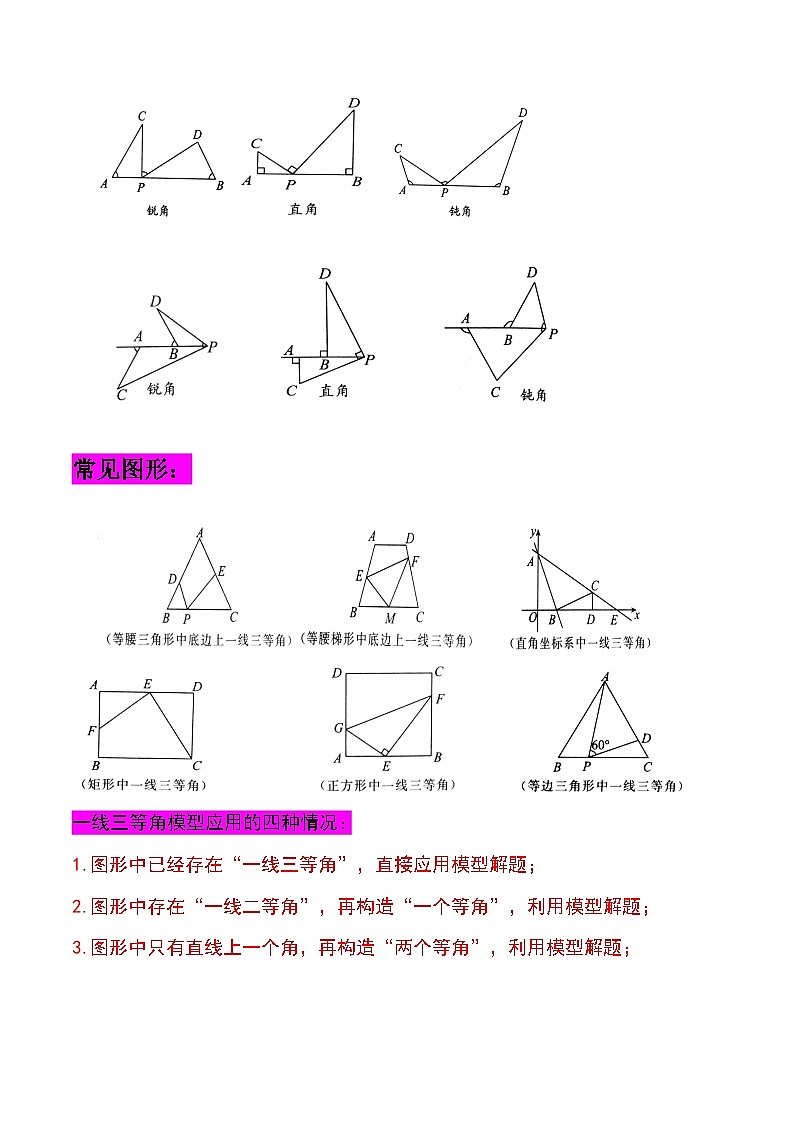
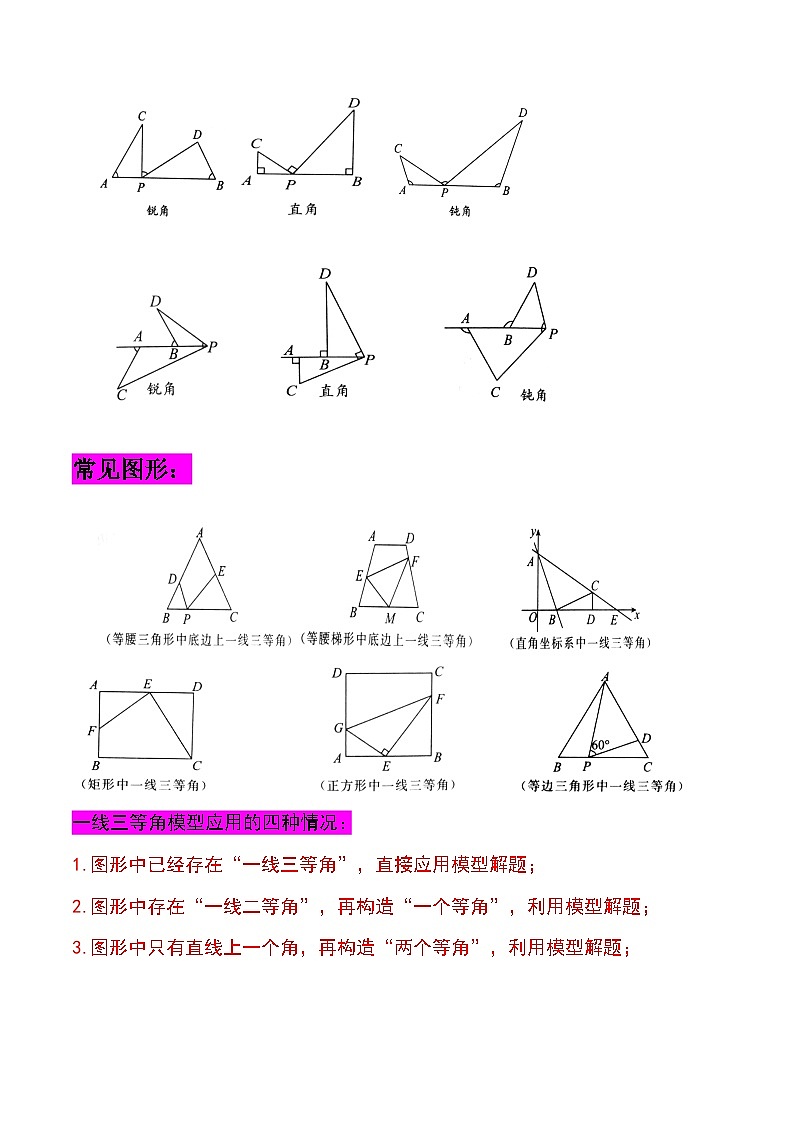
常见图形:
一线三等角模型应用的四种情况:
1.图形中已经存在“一线三等角”,直接应用模型解题;
2.图形中存在“一线二等角”,再构造“一个等角”,利用模型解题;
3.图形中只有直线上一个角,再构造“两个等角”,利用模型解题;
4.图形中只有45°角,直角或直角三角形,可构造“一线三等(直)角”,利用模型解题。
1.(2021·重庆渝北·九年级期末)如图,在等边三角形中,点,分别是边,上的点.将沿翻折,点正好落在线段上的点处,使得.若,则的长度为( )
A.B.C.D.
2.(2021·全国·九年级专题练习)如图,在矩形中,,,、、、分别为矩形边上的点,过矩形的中心,且.为的中点,为的中点,则四边形的周长为( )
A.B.C.D.
1.(2022·江苏扬州·九年级期末)如图,在边长为6的等边△ABC中,D是边BC上一点,将△ABC沿EF折叠使点A与点D重合,若BD : DE=2 : 3,则CF=____.
2.(2021·安徽·淮北市烈山区淮选学校九年级阶段练习)如图,在四边形ABCD中,∠A=∠D=120°,AB=6、AD=4,点E、F分别在线段AD、DC上(点E与点A、D不重合),若∠BEF=120°,AE=x、DF=y,则y关于x的函数关系式为________
3(2021·吉林·长春市绿园区教师进修学校九年级期末)【感知】如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),.易证.(不需要证明)
【探究】如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),.若,,,求AP的长.
【拓展】如图③,在中,,,点P在边AB上(点P不与点A、B重合),连结CP,作,PE与边BC交于点E,当是等腰三角形时,直接写出AP的长.
1.(2020·河南郑州·二模)如图,已知矩形的顶点分别落在轴轴上,,AB=2BC则点的坐标是( )
A.B.C.D.
2.(2020·海南省直辖县级单位·模拟预测)如图,将正方形纸片ABCD沿EF折叠,折痕为EF,点A的对应点是点A′,点B的对应点是点B′,点B′落在边CD上,若CB′:CD=1:3,且BF=10,则EF的长为( )
A.B.C.D.
3.(2022·湖北襄阳·一模)如图,为等边三角形,点D,E分别在边AB,AC上,,将沿直线DE翻折得到,当点F落在边BC上,且时,的值为______.
4.(2022·山东菏泽·三模)(1)问题
如图1,在四边形ABCD中,点P为AB上一点,当时,求证:.
(2)探究
若将90°角改为锐角或钝角(如图2),其他条件不变,上述结论还成立吗?说明理由.
(3)应用
如图3,在中,,,以点A为直角顶点作等腰.点D在BC上,点E在AC上,点F在BC上,且,若,求CD的长.
相关试卷
这是一份中考数学二轮复习几何模拟专项讲练模型43 相似形——旋转相似模型(2份,原卷版+解析版),文件包含中考数学二轮复习几何模拟专项讲练模型43相似形旋转相似模型-原卷版doc、中考数学二轮复习几何模拟专项讲练模型43相似形旋转相似模型-解析版doc等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
这是一份中考数学二轮复习几何模拟专项讲练模型41 相似形——射影定理模型(2份,原卷版+解析版),文件包含中考数学二轮复习几何模拟专项讲练模型41相似形射影定理模型-原卷版doc、中考数学二轮复习几何模拟专项讲练模型41相似形射影定理模型-解析版doc等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
这是一份2024年中考数学几何模型专项复习讲与练 模型43 相似形——旋转相似模型-原卷版+解析,共16页。









