中考数学二轮复习几何模拟专项讲练模型43 相似形——旋转相似模型（2份，原卷版+解析版）

这是一份中考数学二轮复习几何模拟专项讲练模型43 相似形——旋转相似模型（2份，原卷版+解析版），文件包含中考数学二轮复习几何模拟专项讲练模型43相似形旋转相似模型-原卷版doc、中考数学二轮复习几何模拟专项讲练模型43相似形旋转相似模型-解析版doc等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。

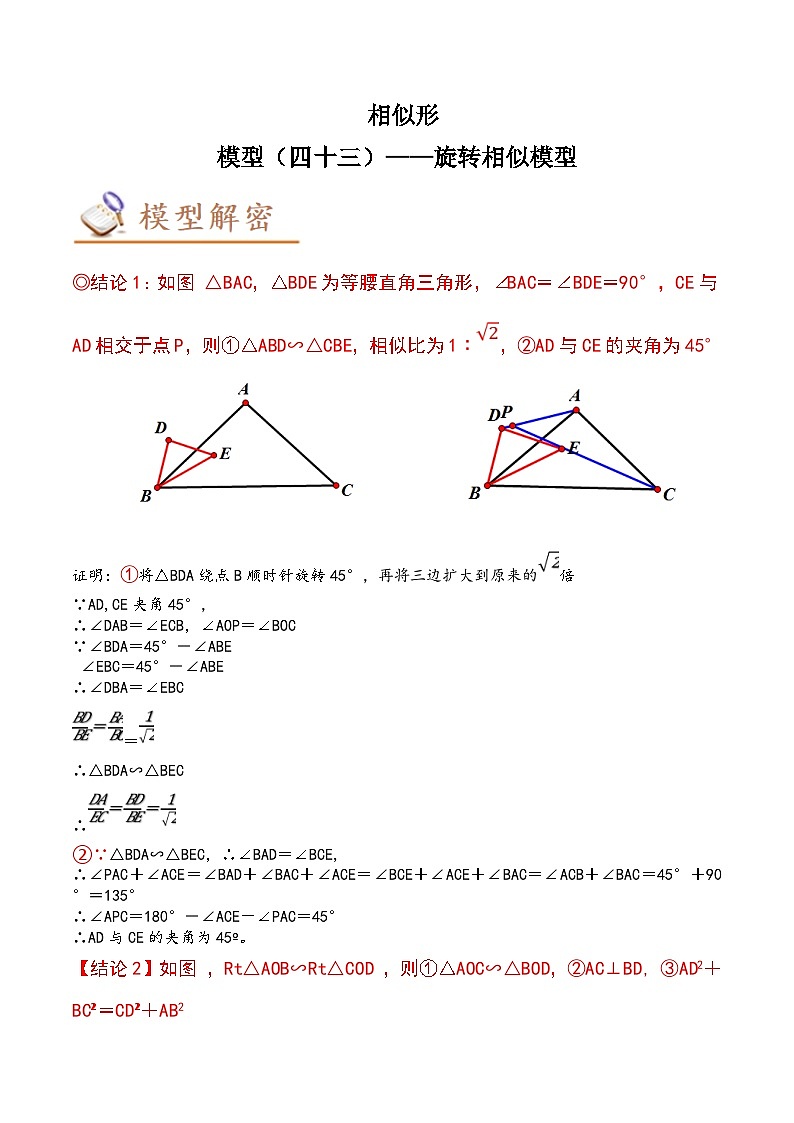
◎结论1：如图 △BAC，△BDE为等腰直角三角形，∠BAC＝∠BDE＝90°，CE与AD相交于点P，则①△ABD∽△CBE，相似比为1∶，②AD与CE的夹角为45°

证明：①将△BDA绕点B顺时针旋转45°，再将三边扩大到原来的倍
∵AD,CE夹角45°，
∴∠DAB＝∠ECB，∠AOP＝∠BOC
∵∠BDA＝45°－∠ABE
∠EBC＝45°－∠ABE
∴∠DBA＝∠EBC
＝
∴△BDA∽△BEC
∴
②∵△BDA∽△BEC，∴∠BAD＝∠BCE,
∴∠PAC＋∠ACE＝∠BAD＋∠BAC＋∠ACE＝∠BCE＋∠ACE＋∠BAC＝∠ACB＋∠BAC＝45°＋90°＝135°
∴∠APC＝180°－∠ACE－∠PAC＝45°
∴AD与CE的夹角为45º。
【结论2】如图 ，Rt△AOB∽Rt△COD ，则①△AOC∽△BOD，②AC⊥BD, ③AD2＋BC²＝CD²＋AB2

【证明】
∵∠AOP＝90°＋∠COB
∠BOD＝90°＋∠COB
∴∠AOP＝∠BOD
∵△AOB∽△COD，∴，∴
∴△AOC∽△BOD
∴∠OAC＝∠OBD
∵∠AMO＝∠BMP
∴∠AOM＝∠BPM＝90°
即AC⊥BD
∵AD²＝PA²＋PD²，BC²＝PB²＋PC2,CD²＝PC²＋PD2,AB²＝PA²＋PB2,
∴AD²＋BC²＝CD²＋AB2
①旋转前有一对相似三角形，旋转后新产生一对相似三角形;
②证明新三角形相似采用"SAS判定法"
③若看不出相似三角形，则需作辅助线构造相似三角形.
eq \\ac(○,巧) eq \\ac(○,记) eq \\ac(○,口) eq \\ac(○,诀)
相同图形在一起，要把边角边想起
1．（2021·全国·九年级专题练习）已知正方形DEFG的顶点F在正方形ABCD的一边AD的延长线上，连结AG，CE交于点H，若，，则CH的长为________.
【答案】
【分析】连接EG，与DF交于N，设CD和AH交于M，证明△ANG∽ADM，得到，从而求出DM的长，再通过勾股定理算出AM的长，通过证明△ADG≌△CDE得到∠DAG=∠DCE，从而说明△ADM∽△CHM，得到，最后算出CH的长.
【详解】解：连接EG，与DF交于N，设CD和AH交于M，
∴∠GNA=90°，DN=FN=EN=GN，
∵∠MAD=∠GAN，∠MDA=∠GNA=90°，
∴△ANG∽ADM，
∴，
∵，
∴DF=EG=2,
∴DN=NG=1，
∵AD=AB=3，
∴，
解得：DM=，
∴MC=，AM=，
∵∠ADM+∠MDG=∠EDG+∠CDG，
∴∠ADG=∠EDC，
在△ADG和△CDE中，
，
∴△ADG≌△CDE（SAS），
∴∠DAG=∠DCE，
∵∠AMD=∠CMH，
∴∠ADM=∠CHM=90°，
∴△ADM∽△CHM，
∴，
即，
解得：CH=.
【点睛】本题考查了全等三角形的判定和性质，相似三角形的判定和性质，正方形的性质，勾股定理，综合性较强，解题的关键是找到合适的全等三角形和相似三角形，通过其性质计算出CH的长.
2．（2022·全国·九年级专题练习）【问题发现】如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是______，位置关系是______；
【探究证明】如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；
【拓展延伸】如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为（0°＜＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．
【答案】BD＝CE，BD⊥CE； BD⊥CE，理由见解析；图见解析，
【分析】（1）证明△BAD≌△CAE，根据全等三角形的性质解答；
（2）连接BD，根据全等三角形的判定和性质以及垂直的定义即可得到结论；
（3）如图3，过A作AF⊥EC，根据相似三角形的判定和性质以及勾股定理即可得到结论．
【详解】解：（1）BD＝CE，BD⊥CE；
（2）BD⊥CE．理由如下：在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，∠AEC＝45°，∵∠CAB＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△CEA≌△BDA，
∴∠BDA＝∠AEC＝45°，∴∠BDE＝∠BDA＋∠ADE＝90°，∴BD⊥CE．
（3）如图所示，过点A作AF⊥CE，垂足为点F．
根据题意可知，Rt△ABC∽Rt△AED，∠BAC＝∠EAD，
∴，∴．
∵∠BAC＝∠EAD＝90°，∴∠BAE＝∠CAD，∴△BAE∽△CAD，
∴∠BEA＝∠CDA，∠BEC＋∠DEA＝∠DEA＋90°，
∴∠BEC＝90°，∴BE⊥CE．
在旋转前，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，
∴，∵AC⊥BD，
∴，∴．
∴，
在Rt△ACD中，CD边上的高，旋转后，得，
∴．
【点睛】本题是几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，等腰三角形的性质等知识点，关键是添加恰当辅助线．
1．（2022·全国·九年级专题练习）在同一平面内，如图①，将两个全等的等腰直角三角形摆放在一起，点A为公共顶点，．如图②，若△ABC固定不动，把△ADE绕点A逆时针旋转，使AD、AE与边BC的交点分别为M、N点M不与点B重合，点N不与点C重合．
【探究】求证：．
【应用】已知等腰直角三角形的斜边长为4．
(1)的值为______．
(2)若，则MN的长为______．
【答案】(1)8
(2)
【探究】利用三角形外角的性质可证，又由，可证明结论；
【应用】（1）首先求出等腰直角三角形的直角边长，再由，得，则；
（2）由，得，由（1）知，得，从而得出答案．
（1）
∵△ABC为等腰直角三角形，，
∴，同理，，
∵，
，
∴，∴；
（2）
（1）∵等腰直角三角形的斜边长为4，
∴，∵，
∴，∴，∴，
故答案为：8；
（2）∵，∴，∵，
∴，∴，
故答案为：．
【点睛】本题是相似形综合题，主要考查了等腰直角三角形的性质，相似三角形的判定与性质，利用前面探索的结论解决新的问题是解题的关键．
1．（2020·广西贵港·模拟预测）在Rt△ABC中，∠BAC＝90°，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，使点C落在C′的位置，C′D交AB于点Q，则的值为（ ）
A．B．C．D．
【答案】A
【分析】根据折叠得到对应线段相等，对应角相等，根据直角三角形的斜边中线等于斜边一半，可得出AD＝DC＝BD，AC＝AC′，∠ADC＝∠ADC′＝45°，CD＝C′D，进而求出∠C、∠B的度数，求出其他角的度数，可得AQ＝AC，将转化为，再由相似三角形和等腰直角三角形的边角关系得出答案．
【详解】解：如图，过点A作AE⊥BC，垂足为E，
∵∠ADC＝45°，
∴△ADE是等腰直角三角形，即AE＝DE＝AD，
在Rt△ABC中，
∵∠BAC＝90°，AD是△ABC的中线，
∴AD＝CD＝BD，
由折叠得：AC＝AC′，∠ADC＝∠ADC′＝45°，CD＝C′D，
∴∠CDC′＝45°+45°＝90°，
∴∠DAC＝∠DCA＝（180°﹣45°）÷2＝67.5°＝∠C′AD，
∴∠B＝90°﹣∠C＝∠CAE＝22.5°，∠BQD＝90°﹣∠B＝∠C′QA＝67.5°，
∴AC′＝AQ＝AC，
由△AEC∽△BDQ得：＝，
∴＝＝＝＝．
故选：A．
【点睛】考查直角三角形的性质，折叠轴对称的性质，以及等腰三角形与相似三角形的性质和判定等知识，合理的转化是解决问题的关键．
2．（2022·河北保定·二模）几何探究：
【问题发现】
（1）如图1所示，△ABC和△ADE是有公共顶点的等边三角形，BD、CE的关系是_______（选填“相等”或“不相等”）；（请直接写出答案）

【类比探究】
（2）如图2所示，△ABC和△ADE是有公共顶点的含有角的直角三角形，（1）中的结论还成立吗?请说明理由；
【拓展延伸】
（3）如图3所示，△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形，将△ADE绕点A自由旋转，若，当B、D、E三点共线时，直接写出BD的长．
【答案】（1）相等；（2）不成立，理由见解析；（3）或．
【分析】（1）证明△ABD≌△ACE（SAS），即可得出；
（2）当在Rt△ADE和Rt△ABC中，，证明△ABD∽△ACE，求出BD与CE的比例；
（3）分两种情况求出BD的长即可．
【详解】（1）相等;
提示：如图4所示．
∵△ADE和△ABC均为等边三角形，
∴
∴
∴
在△ABD和△ACE中，
∴△ABD≌△ACE（SAS）
∴．
（2）不成立；
理由如下：如图5所示．
在Rt△ADE和Rt△ABC中，
∵
∴
∴
∵
∴△ABD∽△ACE
∴
∴
故（1）中的结论不成立；
（3）或．
提示:分为两种情况：
①如图6所示．
易证：△ABD≌△ACE（SAS）
∴
∴
∴
由题意可知：
设,则
在Rt△BCE中,由勾股定理得：
∴
解之得:（舍去）
∴；
②如图7所示．
易证：△ABD≌△ACE（SAS），
设，则
在Rt△BCE中，由勾股定理得：
∴
解之得：（舍去）
∴.
综上所述，或．
【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质、勾股定理、相似三角形的判定与性质等知识，解题的关键是学会运用分类讨论的思想考虑问题．