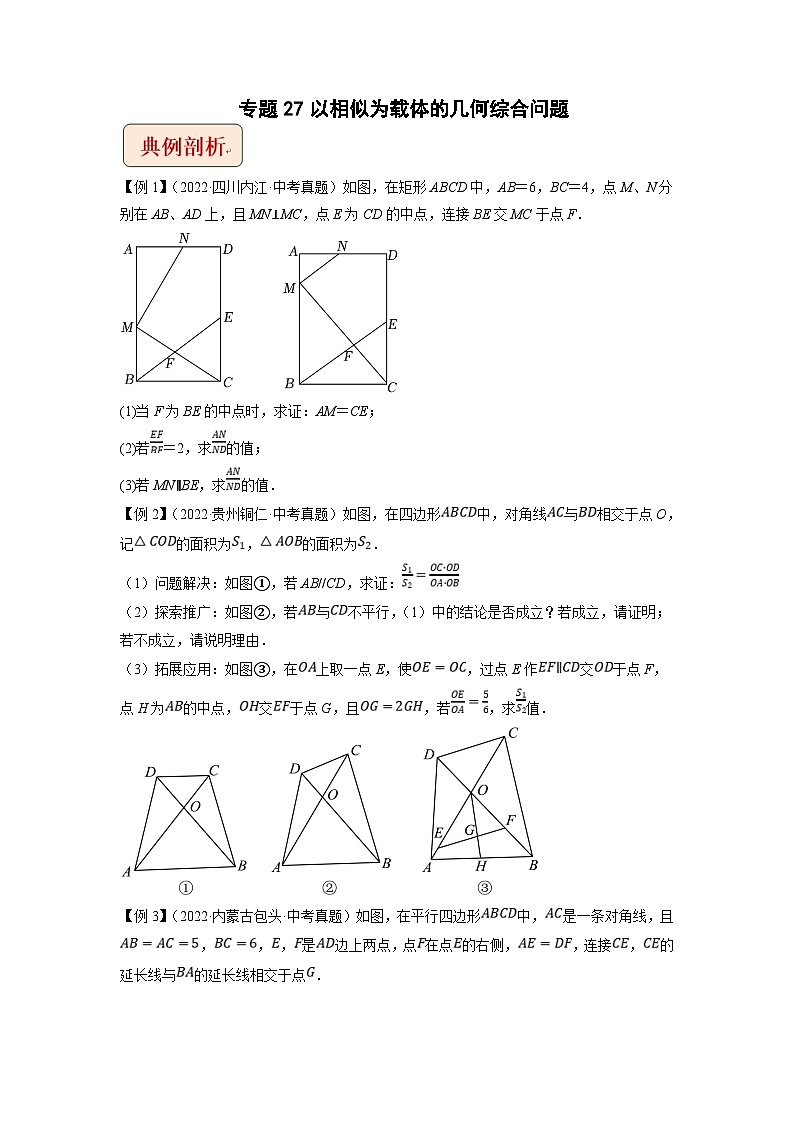

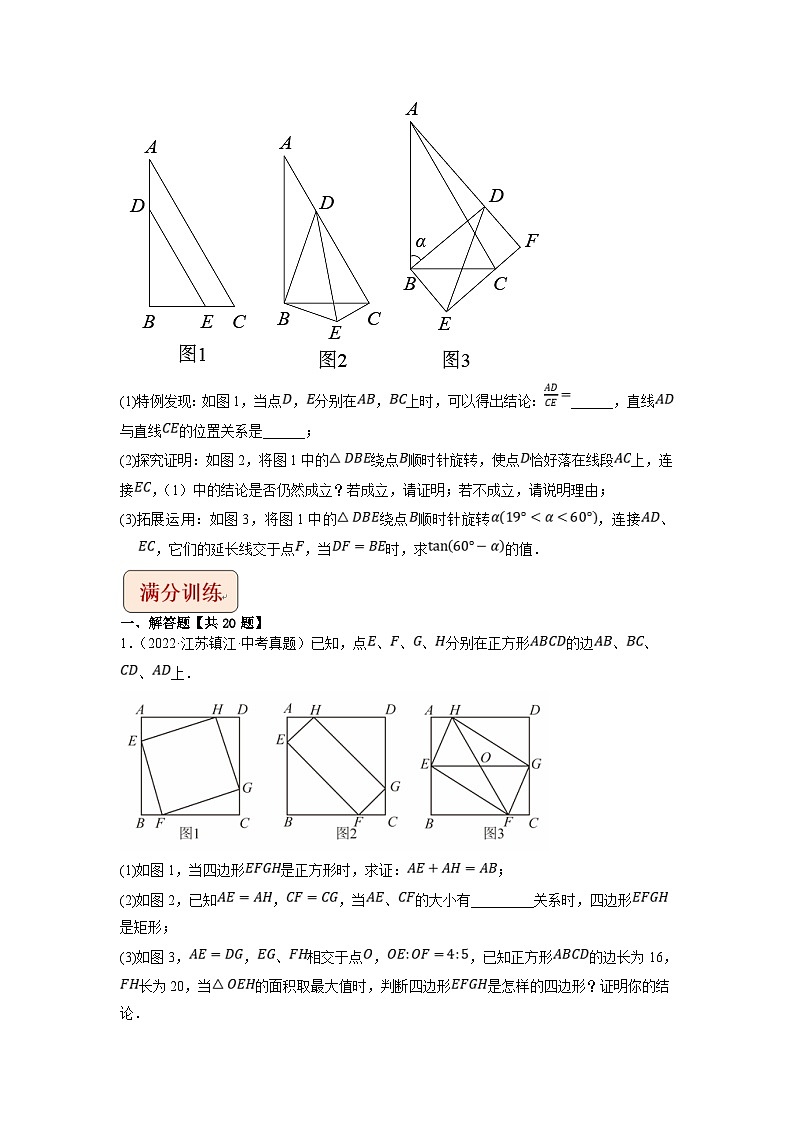



所属成套资源:中考数学二轮复习压轴题培优训练 (2份,原卷版+解析版)
中考数学二轮复习压轴题培优训练专题27以相似为载体的几何综合问题(2份,原卷版+解析版)
展开
这是一份中考数学二轮复习压轴题培优训练专题27以相似为载体的几何综合问题(2份,原卷版+解析版),文件包含中考数学二轮复习压轴题培优训练专题27以相似为载体的几何综合问题原卷版doc、中考数学二轮复习压轴题培优训练专题27以相似为载体的几何综合问题解析版doc等2份试卷配套教学资源,其中试卷共87页, 欢迎下载使用。
(1)当F为BE的中点时,求证:AM=CE;
(2)若=2,求的值;
(3)若MN∥BE,求的值.
【答案】(1)见解析
(2)
(3)
【分析】(1)根据矩形的性质,证明△BMF≌ △ECF,得BM=CE,再利用点E为CD的 中点,即可证明结论;
(2)利用△BMF∽△ECF,得,从而求出BM的长,再利用△ANM∽△BMC ,得 ,求出AN的长,可得答案;
(3)首先利用同角的余角相等得 ∠CBF= ∠CMB,则tan∠CBF=tan∠CMB,得 ,可得BM的长,由(2)同理可得答案.
(1)
证明:∵F为BE的中点,
∴BF=EF,
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD
∴∠BMF=∠ECF,
∵∠BFM=∠EFC,
∴△BMF≌△ECF(AAS),
∴BM=CE,
∵点E为CD的中点,
∴CE=CD,
∵AB=CD,
∴,
∴,
∴AM=CE;
(2)
∵∠BMF=∠ECF,∠BFM=∠EFC,
∴△BMF∽△ECF,
∴,
∵CE=3,
∴BM=,
∴AM=,
∵CM⊥MN,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°,
∵∠AMN+∠ANM=90°,
∴∠ANM=∠BMC,
∵∠A=∠MBC,
∴△ANM∽△BMC,
∴,
∴,
∴,
∴DN=AD﹣AN=4﹣=,
∴;
(3)
∵MN∥BE,
∴∠BFC=∠CMN,
∴∠FBC+∠BCM=90°,
∵∠BCM+∠BMC=90°,
∴∠CBF=∠CMB,
∴tan∠CBF=tan∠CMB,
∴,
∴,
∴,
∴,
由(2)同理得,,
∴,
解得:AN=,
∴DN=AD﹣AN=4﹣=,
∴.
【点睛】本题是相似形综合题,主要考查了矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,三角函数等知识,求出BM的长是解决(2)和(3)的关键.
22.(2022·贵州铜仁·中考真题)如图,在四边形中,对角线与相交于点O,记的面积为,的面积为.
(1)问题解决:如图①,若AB//CD,求证:
(2)探索推广:如图②,若与不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)拓展应用:如图③,在上取一点E,使,过点E作交于点F,点H为的中点,交于点G,且,若,求值.
【答案】(1)见解析;(2)(1)中的结论成立,理由见解析:(3)
【分析】(1)如图所示,过点D作AE⊥AC于E,过点B作BF⊥AC于F,求出,然后根据三角形面积公式求解即可;
(2)同(1)求解即可;
(3)如图所示,过点A作交OB于M,取BM中点N,连接HN,先证明△OEF≌△OCD,得到OD=OF,证明△OEF∽△OAM,得到,设,则,证明△OGF∽△OHN,推出,,则,由(2)结论求解即可.
【详解】解:(1)如图所示,过点D作AE⊥AC于E,过点B作BF⊥AC于F,
∴,
∴,
,
∵∠DOE=∠BOF,
∴;
∴;
(2)(1)中的结论成立,理由如下:
如图所示,过点D作AE⊥AC于E,过点B作BF⊥AC于F,
∴,
∴,
,
∵∠DOE=∠BOF,
∴;
∴;
(3)如图所示,过点A作交OB于M,取BM中点N,连接HN,
∵,
∴∠ODC=∠OFE,∠OCD=∠OEF,
又∵OE=OC,
∴△OEF≌△OCD(AAS),
∴OD=OF,
∵,
∴△OEF∽△OAM,
∴,
设,则,
∵H是AB的中点,N是BM的中点,
∴HN是△ABM的中位线,
∴,
∴△OGF∽△OHN,
∴,
∵OG=2GH,
∴,
∴,
∴,,
∴,
由(2)可知.
【点睛】本题主要考查了解直角三角形,相似三角形的性质与判定,全等三角形的性质与判定,三角形中位线定理,正确作出辅助线是解题的关键.
23.(2022·内蒙古包头·中考真题)如图,在平行四边形中,是一条对角线,且,,,是边上两点,点在点的右侧,,连接,的延长线与的延长线相交于点.
(1)如图1,是边上一点,连接,,与相交于点.
①若,求的长;
②在满足①的条件下,若,求证:;
(2)如图2,连接,是上一点,连接.若,且,求的长.
【答案】(1)①;②证明见解析
(2)
【分析】(1)①解:根据平行四边形的性质可证,得到,再根据,,,结合平行四边形的性质求出的长,代入比例式即可求出的长;
②先根据证明可得,再根据,求出,进一步证明,最后利用等腰三角形的三线合一可证明结论.
(2)如图,连接,先根据证明,再结合,说明,利用平行线分线段成比例定理可得,接着证明,可得到,设,则,根据构建方程求出,最后利用可得结论.
(1)
①解:如图,
∵四边形是平行四边形,,,
∴,,,,
∴,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴的长为.
②证明:∵,
∴,
∵,
在和中,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
(2)
如图,连接,
∵,,
∴,
∴,
∵,
在和中,
∴,
∴,
∴
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
设,则,
∵,
∴,
∴,
即,
∴,
∴.
∴的长为.
【点睛】本题考查了平行四边形的性质,相似三角形的判定及性质,全等三角形的判定及性质,等腰三角形的三线合一,平行线的判定及性质,平行线分线段成比例定理等知识.灵活运用相似三角形和全等三角形的判定及性质是解答本题的关键.
24.(2022·江苏泰州·中考真题)已知:△ABC中,D 为BC边上的一点.
(1)如图①,过点D作DE∥AB交AC边于点E,若AB=5,BD=9,DC=6,求DE的长;
(2)在图②,用无刻度的直尺和圆规在AC边上做点F,使∠DFA=∠A;(保留作图痕迹,不要求写作法)
(3)如图③,点F在AC边上,连接BF、DF,若∠DFA=∠A,△FBC的面积等于,以FD为半径作⊙F,试判断直线BC与⊙F的位置关系,并说明理由.
【答案】(1)2
(2)图见详解
(3)直线BC与⊙F相切,理由见详解
【分析】(1)由题意易得,则有,然后根据相似三角形的性质与判定可进行求解;
(2)作DT∥AC交AB于点T,作∠TDF=∠ATD,射线DF交AC于点F,则点F即为所求;
(3)作BR∥CF交FD的延长线于点R,连接CR,证明四边形ABRF是等腰梯形,推出AB=FR,由CF∥BR,推出,推出CD⊥DF,然后问题可求解.
(1)
解:∵DE∥AB,
∴,
∴,
∵AB=5,BD=9,DC=6,
∴,
∴;
(2)
解:作DT∥AC交AB于点T,作∠TDF=∠ATD,射线DF交AC于点F,则点F即为所求;
如图所示:点F即为所求,
(3)
解:直线BC与⊙F相切,理由如下:
作BR∥CF交FD的延长线于点R,连接CR,如图,
∵∠DFA=∠A,
∴四边形ABRF是等腰梯形,
∴,
∵△FBC的面积等于,
∴,
∴CD⊥DF,
∵FD是⊙F的半径,
∴直线BC与⊙F相切.
【点睛】本题主要考查相似三角形的性质与判定、平行线的性质与判定及切线的判定,熟练掌握相似三角形的性质与判定、平行线的性质与判定及切线的判定是解题的关键.
25.(2022·湖南岳阳·中考真题)如图,和的顶点重合,,,,.
(1)特例发现:如图1,当点,分别在,上时,可以得出结论:______,直线与直线的位置关系是______;
(2)探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)拓展运用:如图3,将图1中的绕点顺时针旋转,连接、,它们的延长线交于点,当时,求的值.
【答案】(1) ,垂直
(2)成立,理由见解析
(3)
【分析】(1)解直角三角形求出,,可得结论;
(2)结论不变,证明,推出,,可得结论;
(3)如图3中,过点作于点,设交于点,过点作于点求出,,可得结论.
(1)
解:在中,,,,
∴,
在中,,,
∴,
∴,,
∴,此时,
故答案为:,垂直;
(2)
结论成立.
理由:∵,
∴,
∵,,
∴,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
∴;
(3)
如图3中,过点作于点,设交于点,过点作于点.
∵,,
∴,
∴.
∵,
∴,,
当时,四边形是矩形,
∴,,
设,则,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴.
【点睛】本题属于三角形综合题,考查了解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.
一、解答题
1.(2022·江苏镇江·中考真题)已知,点、、、分别在正方形的边、、、上.
(1)如图1,当四边形是正方形时,求证:;
(2)如图2,已知,,当、的大小有_________关系时,四边形是矩形;
(3)如图3,,、相交于点,,已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.
【答案】(1)见解析
(2)
(3)平行四边形,证明见解析
【分析】(1)利用平行四边形的性质证得,根据角角边证明.
(2)当,证得,是等腰直角三角形,∠HEF=∠EFG=90°,即可证得四边形EFGH是矩形.
(3)利用正方形的性质证得为平行四边形,过点作,垂足为点,交于点,由平行线分线段成比例,设,,,则可表示出,从而把△OEH的面积用x的代数式表示出来,根据二次函数求出最大值,则可得OE=OG,OF=OH,即可证得平行四边形.
(1)
∵四边形为正方形,
∴,
∴.
∵四边形为正方形,
∴,,
∴,
∴.
在和中,
∵,,,
∴.
∴.
∴;
(2)
;证明如下:
∵四边形为正方形,
∴,AB=BC=AD=CD,
∵AE=AH,CF=CG,AE=CF,
∴AH=CG,
∴,
∴EH=FG.
∵AE=CF,
∴AB-AE=BC-CF,即BE=BF,
∴是等腰直角三角形,
∴∠BEF=∠BFE=45°,
∵AE=AH,CF=CG,
∴∠AEH=∠CFG=45°,
∴∠HEF=∠EFG=90°,
∴EH∥FG,
∴四边形EFGH是矩形.
(3)
∵四边形为正方形,
∴.
∵,,
∴四边形为平行四边形.
∴.
∴.
过点作,垂足为点,交于点,
∴.
∵,
设,,,则,
∴.
∴.
∴当时,的面积最大,
∴,,
∴四边形是平行四边形.
【点睛】此题考查了正方形的性质,矩形的判定和平行四边形的性质与判定,平行线分线段成比例定理,全等三角形的判定与性质,等腰三角形的性质,二次函数的最值,有一定的综合性,解题的关键是熟悉这些知识并灵活运用.
2.(2022·山东东营·中考真题)和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是____________,位置关系是____________;
(2)如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;
(3)当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.
【答案】(1)CD=EF,CD∥EF
(2)CD=EF,CD∥EF,成立,理由见解析
(3)点D运动到BC的中点时,是菱形,证明见解析
【分析】(1)根据和均为等边三角形,得到AF=AD,AB=BC,∠FAD=∠ABC=60°,根据E、D分别与点A、B重合,得到AB=AD,EF=AF,CD=BC,∠FAD=∠FAB,推出CD=EF,CD∥EF;
(2)连接BF,根据∠FAD=∠BAC=60°,推出∠FAB=∠DAC,根据AF=AD,AB=AC,推出△AFB≌△ADC,得到∠ABF=∠ACD=60°,BF=CD,根据AE=BD,推出BE=CD,得到BF=BE,推出△BFE是等边三角形,得到BF=EF,∠FEB=60°,推出CD=EF, CD∥EF;
(3)过点E作EG⊥BC于点G,设△ABC的边长为a,AD=h,根据AB=BC,BD=CD= BC= a, BD=AE,推出AE=BE= AB,根据AB=AC, 推出AD⊥BC,得到EG∥AD,推出△EBG∽△ABD,推出,得到= h,根据CD=EF, CD∥EF,推出四边形CEFD是平行四边形,推出,根据EF=BD,EF∥BD,推出四边形BDEF是平行四边形,根据BF=EF,推出是菱形.
(1)
∵和均为等边三角形,
∴AF=AD,AB=BC,∠FAD=∠ABC=60°,
当点E、D分别与点A、B重合时,AB=AD,EF=AF,CD=BC,∠FAD=∠FAB,
∴CD=EF,CD∥EF;
故答案为:CD=EF,CD∥EF;
(2)
CD=EF,CD∥EF,成立.
证明:
连接BF,
∵∠FAD=∠BAC=60°,
∴∠FAD-∠BAD=∠BAC-∠BAD,
即∠FAB=∠DAC,
∵AF=AD,AB=AC,
∴△AFB≌△ADC(SAS),
∴∠ABF=∠ACD=60°,BF=CD,
∵AE=BD,
∴BE=CD,
∴BF=BE,
∴△BFE是等边三角形,
∴BF=EF,∠FEB=60°,
∴CD=EF,BC∥EF,
即CD∥EF,
∴CD=EF, CD∥EF;
(3)
如图,当点D运动到BC的中点时,四边形的面积是面积的一半,此时,四边形是菱形.
证明:
过点E作EG⊥BC于点G,设△ABC的边长为a,AD=h,
∵AB=BC,BD=CD= BC= a, BD=AE,
∴AE=BE= AB,
∵AB=AC,
∴AD⊥BC,
∴EG∥AD,
∴△EBG∽△ABD,
∴,
∴= h,
由(2)知,CD=EF, CD∥EF,
∴四边形CEFD是平行四边形,
∴,
此时,EF=BD,EF∥BD,
∴四边形BDEF是平行四边形,
∵BF=EF,
∴是菱形.
【点睛】本题主要考查了等边三角形判定与性质,全等三角形的判定与性质,平行四边形的判定与性质,相似三角形的判定与性质,菱形的判定,解决问题的关键是熟练掌握等边三角形的判定和性质,全等三角形的判定和性质,平行四边形判定和性质,相似三角形的判定和性质,菱形的判定.
3.(2022·辽宁鞍山·中考真题)如图,在中,,,点在直线上,连接,将绕点逆时针旋转,得到线段,连接,.
(1)求证:;
(2)当点在线段上(点不与点,重合)时,求的值;
(3)过点作交于点,若,请直接写出的值.
【答案】(1)证明见解析;
(2)
(3)或
【分析】(1)作AH⊥BC于H,可得BH=AB,BC=2BH,进而得出结论;
(2)证明△ABD∽△CBE,进而得出结果;
(3)当点D在线段AC上时,作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,设AB=AC=3a,则AD=2a,解直角三角形BDF,求得BD的长,根据△DAG∽△DBF求得AQ,进而求得AN,进一步得出结果;当点D在AC的延长线上时,设AB=AC=2a,则AD=4a,同样方法求得结果.
(1)
证明:如图1,
作AH⊥BC于H,
∵AB=AB,
∴∠BAH=∠CAH=∠BAC=×120°=60°,BC=2BH,
∴sin60°=,
∴BH=AB,
∴BC=2BH=AB;
(2)
解:∵AB=AC,
∴∠ABC=∠ACB=,
由(1)得,,
同理可得,
∠DBE=30°,,
∴∠ABC=∠DBE,,
∴∠ABC−∠DBC=∠DBE−∠DBC,
∴∠ABD=∠CBE,
∴△ABD∽△CBE,
∴;
(3)
:如图2,
当点D在线段AC上时,
作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,
设AB=AC=3a,则AD=2a,
由(1)得,,
在Rt△ABF中,∠BAF=180°−∠BAC=60°,AB=3a,
∴AF=3a•cs60°=,BF=3a•sin60°=,
在Rt△BDF中,DF=AD+AF=,
,
∵∠AGD=∠F=90°,∠ADG=∠BDF,
∴△DAG∽△DBF,
∴,
∴,
∴,
∵ANDE,
∴∠AND=∠BDE=120°,
∴∠ANG=60°,
∴,
∴,
如图3,
当点D在AC的延长线上时,
设AB=AC=2a,则AD=4a,
由(1)得,
CE=,
作BR⊥CA,交CA的延长线于R,作AQ⊥BD于Q,
同理可得,
AR=a,BR=,
∴,
∴,
∴,
∴,
∴,
综上所述:的值为或.
【点睛】本题考查了等腰三角形的性质,相似三角形的判定和性质,解直角三角形等知识,解决问题的关键是正确分类和较强的计算能力.
4.(2022·浙江衢州·中考真题)如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结交于点,平分交于点G.
(1)求证:.
(2)若.
①求菱形的面积.
②求的值.
(3)若,当的大小发生变化时(),在上找一点,使为定值,说明理由并求出的值.
【答案】(1)见解析
(2)①24,②
(3)=,理由见解析
【分析】(1)由菱形的性质可证得∠CBD=∠ABD=∠ABC,由平分交于点G,得到∠CBG=∠EBG=∠CBE,进一步即可得到答案;
(2)①连接AC交BD于点O,Rt△DOC中,OC=,求得AC=8,由菱形的面积公式可得答案;②由BGAC,得到,DH=HG,DG=2DH,又由DG=2GE,得到EG=DH=HG,则,再证明△CDH∽△AEH,CH=AC=,OH=OC-CH=4-=,利用正切的定义得到答案;
(3)过点G作GTBC,交AE于点T,△BGE∽△AHE,得AB=BE=5,则EG=GH,再证△DOH∽△DBG,得DH=GH=EG,由△EGT∽△EDA得,GT=,为定值,即可得到ET的值.
(1)
证明:∵四边形ABCD是菱形,
∴BC=DC,ABCD,
∴∠BDC=∠CBD,∠BDC=∠ABD,
∴∠CBD=∠ABD=∠ABC,
∵平分交于点G,
∴∠CBG=∠EBG=∠CBE,
∴∠CBD+∠CBG=(∠ABC+∠CBE)=×180°=90°,
∴∠DBG=90°;
(2)
解:①如图1,连接AC交BD于点O,
∵四边形ABCD是菱形,BD=6,
∴OD=BD=3,AC⊥BD,
∴∠DOC=90°,
在Rt△DOC中,OC=,
∴AC=2OC=8,
∴,
即菱形的面积是24.
②如图2,连接AC,分别交BD、DE于点O、H,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵∠DBG=90°
∴BG⊥BD,
∴BGAC,
∴,
∴DH=HG,DG=2DH,
∵DG=2GE,
∴EG=DH=HG,
∴,
∵ABCD,
∴∠DCH=EAH,∠CDH=∠AEH,
∴△CDH∽△AEH,
∴,
∴CH=AC=,
∴OH=OC-CH=4-=,
∴tan∠BDE=;
(3)
如图3,过点G作GTBC交AE于点T,此时ET=.
理由如下:由题(1)可知,当∠DAB的大小发生变化时,始终有BGAC,
∴△BGE∽△AHE,
∴,
∵AB=BE=5,
∴EG=GH,
同理可得,△DOH∽△DBG,
∴,
∵BO=DO,
∴DH=GH=EG,
∵GTBC,
∴GTAD,
∴△EGT∽△EDA,
∴,
∵AD=AB=5,
∴GT=,为定值,
此时ET=AE=(AB+BE)=.
【点睛】此题主要考查了相似三角形的判定和性质、菱形的性质、勾股定理、锐角三角函数等知识,熟练掌握相似三角形的判定和性质是解题的关键.
5.(2022·山东枣庄·中考真题)已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.
(1)如图①,若PQ⊥BC,求t的值;
(2)如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?
【答案】(1)当t=2时,PQ⊥BC
(2)当t的值为时,四边形QPCP′为菱形
【分析】(1)根据勾股定理求出,根据相似三角形的性质列出比例式,计算即可.
(2)作于,于,证明出为直角三角形,进一步得出和为等腰直角三角形,再证明四边形为矩形,利用勾股定理在、中,结合四边形为菱形,建立等式进行求解.
【详解】(1)解:(1)如图①,
∵∠ACB=90°,AC=BC=4cm,
∴AB==(cm),
由题意得,AP=tcm,BQ=tcm,
则BP=(4﹣t)cm,
∵PQ⊥BC,
∴∠PQB=90°,
∴∠PQB=∠ACB,
∴PQAC,
,
,
∴=,
∴,
解得:t=2,
∴当t=2时,PQ⊥BC.
(2)解:作于,于,如图,
,,
,,
为直角三角形,
,
和为等腰直角三角形,
,,
,
四边形为矩形,
,
,
,
在中,,
在中,,
四边形为菱形,
,
,
,(舍去).
的值为.
【点睛】此题是相似形综合题,主要考查的是菱形的性质、等腰直角三角形的性质,线段垂直平分线的性质,用方程的思想解决问题是解本题的关键.
6.(2022·江苏南通·中考真题)如图,矩形中,,点E在折线上运动,将绕点A顺时针旋转得到,旋转角等于,连接.
(1)当点E在上时,作,垂足为M,求证;
(2)当时,求的长;
(3)连接,点E从点B运动到点D的过程中,试探究的最小值.
【答案】(1)见详解
(2)或
(3)
【分析】(1)证明即可得证.
(2)分情况讨论,当点E在BC上时,借助,在中求解;当点E在CD上时,过点E作EG⊥AB于点G,FH⊥AC于点H,借助并利用勾股定理求解即可.
(3)分别讨论当点E在BC和CD上时,点F所在位置不同,DF的最小值也不同,综合比较取最小即可.
(1)
如图所示,
由题意可知,,,
,
由旋转性质知:AE=AF,
在和中,
,
,
.
(2)
当点E在BC上时,
在中,,,
则,
在中,,,
则,
由(1)可得,,
在中,,,
则,
当点E在CD上时,如图,
过点E作EG⊥AB于点G,FH⊥AC于点H,
同(1)可得,
,
由勾股定理得;
故CF的长为或.
(3)
如图1所示,当点E在BC边上时,过点D作于点H,
由(1)知,,
故点F在射线MF上运动,且点F与点H重合时,DH的值最小.
在与中,
,
,
,
即,
,,
,
在与中,
,
,
,
即,
,
故的最小值;
如图2所示,当点E在线段CD上时,将线段AD绕点A顺时针旋转的度数,得到线段AR,连接FR,过点D作,,
由题意可知,,
在与中,
,
,
,
故点F在RF上运动,当点F与点K重合时,DF的值最小;
由于,,,
故四边形DQRK是矩形;
,
,
,
,
故此时DF的最小值为;
由于,故DF的最小值为.
【点睛】本题考查矩形的性质、全等三角形的判定和性质、相似三角形的性质和判定、勾股定理、解直角三角形,解决本题的关键是各性质定理的综合应用.
7.(2022·山东菏泽·中考真题)如图1,在中,于点D,在DA上取点E,使,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将绕点D旋转,得到(点,分别与点B,E对应),连接,在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;
(3)如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若,求的长.
【答案】(1)CE⊥AB,理由见解析
(2)一致,理由见解析
(3)
【分析】(1)由等腰直角三角形的性质可得∠ABC=∠DAB=45°,∠DCE=∠DEC=∠AEH=45°,可得结论;
(2)通过证明,可得,由余角的性质可得结论;
(3)由等腰直角的性质和直角三角形的性质可得,即可求解.
【详解】(1)如图,延长CE交AB于H,
∵∠ABC=45°,AD⊥BC,
∴∠ADC=∠ADB=90°,∠ABC=∠DAB=45°,
∵DE=CD,
∴∠DCE=∠DEC=∠AEH=45°,
∴∠BHC=∠BAD+∠AEH=90°,
∴CE⊥AB;
(2)在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是一致的,理由如下:
如图2,延长交于H,
由旋转可得:CD=,=AD,
∵∠ADC=∠ADB=90°,
∴,
∵,
∴,
,
∵+∠DGC=90°,∠DGC=∠AGH,
∴∠DA+∠AGH=90°,
∴∠AHC=90°,
;
(3)如图3,过点D作DH于点H,
∵△BED绕点D顺时针旋转30°,
∴,
,
,
∴AD=2DH,AH=DH=,
,
由(2)可知:,
,
∵AD⊥BC,CD=,
∴DG=1,CG=2DG=2,
∴CG=FG=2,
,
∴AG=2GF=4,
∴AD=AG+DG=4+1=5,
∴.
【点睛】本题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,旋转的性质,相似三角形的判定和性质等知识,证明三角形相似是解题的关键.
8.(2022·辽宁丹东·中考真题)已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.
(1)如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;
(2)如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;
(3)如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB=,∠AEB=45°,请直接写出△MND的面积.
【答案】(1)BE=DG,BE⊥DG
(2)BE=,BE⊥DG,理由见解析
(3)S△MNG=
【分析】(1)证明△BAE≌△DAG,进一步得出结论;
(2)证明BAE∽△DAG,进一步得出结论;
(3)解斜三角形ABE,求得BE=3,根据(2)可得DG=6,从而得出三角形BEG的面积,可证得△MND≌△MNG,△MNG与△BEG的面积比等于1:4,进而求得结果.
(1)
解:由题意得:四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD﹣∠DAE=∠EAG﹣∠DAE,
∴∠BAE=∠DAG,
∴△BAE≌△DAG(SAS),
∴BE=DG,∠ABE=∠ADG,
∴∠ADG+∠ADB=∠ABE+∠ADB=90°,
∴∠BDG=90°,
∴BE⊥DG;
(2)
BE=,BE⊥DG,理由如下:
由(1)得:∠BAE=∠DAG,
∵==2,
∴△BAE∽△DAG,
∴,∠ABE=∠ADG,
∴∠ADG+∠ADB=∠ABE+∠ADB=90°,
∴∠BDG=90°,
∴BE⊥DG;
(3)
如图,
作AH⊥BD于H,
∵tan∠ABD=,
∴设AH=2x,BH=x,
在Rt△ABH中,
x2+(2x)2=()2,
∴BH=1,AH=2,
在Rt△AEH中,
∵tan∠ABE=,
∴,
∴EH=AH=2,
∴BE=BH+EH=3,
∵BD==5,
∴DE=BD﹣BE=5﹣3=2,
由(2)得:,DG⊥BE,
∴DG=2BE=6,
∴S△BEG===9,
在Rt△BDG和Rt△DEG中,点M是BG的中点,点N是CE的中点,
∴DM=GM=,
∵NM=NM,
∴△DMN≌△GMN(SSS),
∵MN是△BEG的中位线,
∴MNBE,
∴△BEG∽△MNG,
∴=()2=,
∴S△MNG=S△MNG=S△BEG=.
【点睛】本题主要考查了正方形,矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是类比的方法.
9.(2022·山东济南·中考真题)如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
(1)判断线段BD与CE的数量关系并给出证明;
(2)延长ED交直线BC于点F.
①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为_______;
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.
【答案】(1),理由见解析
(2)①;②,理由见解析
【分析】(1)利用等边三角形的性质和旋转的性质易得到,再由全等三角形的性质求解;
(2)①根据线段绕点A按逆时针方向旋转得到得到是等边三角形,
由等边三角形的性质和(1)的结论来求解;②过点A作于点G,连接AF,根据等边三角形的性质和锐角三角函数求值得到,,进而得到,进而求出,结合,ED=EC得到,再用等腰直角三角形的性质求解.
(1)
解:.
证明:∵是等边三角形,
∴,.
∵线段绕点A按逆时针方向旋转得到,
∴,,
∴,
∴,
即.
在和中
,
∴,
∴;
(2)
解:①
理由:∵线段绕点A按逆时针方向旋转得到,
∴是等边三角形,
∴,
由(1)得,
∴;
②过点A作于点G,连接AF,如下图.
∵是等边三角形,,
∴,
∴.
∵是等边三角形,点F为线段BC中点,
∴,,,
∴,
∴,,
∴,
即,
∴,
∴.
∵,,
∴,
即是等腰直角三角形,
∴.
【点睛】本题主要考查了等边三角形的性质,旋转的性质,全等三角形的判定和性质,解直角三角形,相似三角形的判定和性质,等腰直角三角形的判定和性质,理解相关知识是解答关键.
10.(2022·湖南益阳·中考真题)如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.
(1)直接写出图中与△AFB相似的一个三角形;
(2)若四边形AFCC′是平行四边形,求CE的长;
(3)当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?
【答案】(1)答案不唯一,如△AFB∽△BCE
(2)CE=7.5
(3)当CE的长为长为或3时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形
【分析】(1)因为△AFB是直角三角形,所以和它相似的三角形都是直角三角形,有三个直角三角形和△AFB相似,解答时任意写出一个即可;
(2)根据△AFB∽△BGC,得,即,设AF=5x,BG=3x,根据△AFB∽△BCE∽△BGC,列比例式可得CE的长;
(3)分两种情况:①当C'F=BC'时,如图2,②当C'F=BF时,如图3,根据三角形相似列比例式可得结论.
(1)解:(任意回答一个即可);①如图1,△AFB∽△BCE,理由如下:∵四边形ABCD是矩形,∴DC∥AB,∠BCE=∠ABC=90°,∴∠BEC=∠ABF,∵AF⊥BE,∴∠AFB=90°,∴∠AFB=∠BCE=90°,∴△AFB∽△BCE;②△AFB∽△CGE,理由如下:∵CG⊥BE,∴∠CGE=90°,∴∠CGE=∠AFB,∵∠CEG=∠ABF,∴△AFB∽△CGE;③△AFB∽△BGC,理由如下:∵∠ABF+∠CBG=∠CBG+∠BCG=90°,∴∠ABF=∠BCG,∵∠AFB=∠CGB=90°,∴△AFB∽△BGC;
(2)∵四边形AFCC'是平行四边形,∴AF=CC',由(1)知:△AFB∽△BGC,∴ ,即,设AF=5x,BG=3x,∴CC'=AF=5x,∵CG=C'G,∴CG=C'G=2.5x,∵△AFB∽△BCE∽△BGC,∴ ,即,∴CE=7.5;
(3)分两种情况:①当C'F=BC'时,如图2,∵C'G⊥BE,∴BG=GF,∵CG=C'G,∴四边形BCFC'是菱形,∴CF=CB=9,由(2)知:设AF=5x,BG=3x,∴BF=6x,∵△AFB∽△BCE,∴ ,即,∴,∴CE=;②当C'F=BF时,如图3,由(1)知:△AFB∽△BGC,∴ ,设BF=5a,CG=3a,∴C'F=5a,∵CG=C'G,BE⊥CC',∴CF=C'F=5a,∴FG==4a,∵tan∠CBE=,∴,∴CE=3;综上,当CE的长为长为或3时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形.
【点睛】本题是四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,相似三角形的判定和性质,平行线的性质,等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
11.(2022·四川绵阳·中考真题)如图,平行四边形ABCD中,DB=,AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动.
(1)如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;
(2)如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?
(3)如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.
【答案】(1);
(2)y关于x的函数解析式为;当时,y的最大值为;
(3)当EF∥BD时,能使EM=HM.理由见解析
【分析】(1)延长DF交CB的延长线于点G,先证得,可得,根据题意可得AF=,AE=,可得到CG=3,再证明△PDE∽△PGC,即可求解;
(2)分三种情况讨论:当0≤x≤2时,E点在AD上,F点在AB上;当时,E点在BD上,F点在AB上;当时,点E、F均在BD上,即可求解;
(3)当EF∥BD时,能使EM=HM.理由:连接DH,根据直角三角形的性质,即可求解 .
(1)
解:如图,延长DF交CB的延长线于点G,
∵四边形ABCD是平行四边形,
∴,
∴,
∴,
∵点E的速度为1个单位每秒,点F的速度为4个单位每秒,运动时间为秒,
∴AF=,AE=,
∵AB=4,AD=2,
∴BF=, ED=,
∴,
∴BG=1,
∴CG=3,
∵,
∴△PDE∽△PGC,
∴,
∴;
(2)
解:根据题意得:当0≤x≤2时,E点在AD上,F点在AB上,此时AE=x,,
∵, AB=4,AD=2,
∴,
∴△ABD是直角三角形,
∵,
∴∠ABD=30°,
∴∠A=60°,
如图,过点E作交于H,
∴,
∴;
∴当x>0时,y随x的增大而增大,
此时当x=2时,y有最大值3;
当时,E点在BD上,F点在AB上,
如图, 过点E作交于N,过点D作交于M,则EN∥DM,
根据题意得:DE=x-2,
∴,
在Rt△ABD中,,AM=1,
∵EN∥DM,
∴△BEN∽△BDM,
∴,
∴
∴,
∴,
此时该函数图象的对称轴为直线 ,
∴当时,y随x的增大而增大,
此时当时,y有最大值;
当时,点E、F均在BD上,
过点E作交于Q,过点F作交于P,过点D作DM⊥AB于点M,
∴,DA+DE=x,
∵AB=4,AD=2,
∴,,
∵PF∥DM,
∴△BFP∽△BDM,
∴,即,
∴,
∵,
∴△BEQ∽△BDM,
∴,即,
∴,
∴,
此时y随x的增大而减小,
此时当时,y有最大值;
综上所述:y关于x的函数解析式为
当时,y最大值为;
(3)
解:当EF∥BD时,能使EM=HM.理由如下:
连接DH,如图,
∵,AB=4,
∴.AH=1,
由(2)得:此时,
∵M是DF的中点,
∴HM=DM=MF,
∵EF∥BD,BD⊥AD,
∴EF⊥AD,
∴EM=DM=FM,
∴EM=HM.
【点睛】本题是四边形的综合题,熟练掌握平行四边形的性质,平行线的性质,直角三角形的性质,分类讨论,数形结合是解题的关键.
12.(2022·山东济宁·中考真题)如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF.
(1)填空:若△AOD是等腰三角形,则点D的坐标为 ;
(2)当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.
①求m值最大时点D的坐标;
②是否存在这样的m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.
【答案】(1)或
(2)①点D坐标为;②存在,
【分析】(1)根据题意易得∠AOB=60°从而∠AOC=30°和∠CDA=60°,根据tan30°求得AC的长,再根据sin60°求得AD的长,当OA=AD和OD=OA时分情况讨论,即可得到OD的长,从而得到D点坐标;
(2)①设点D的坐标为(0,a),则OD=a,CD=-a,易证,从而得出,代入即可得到m与a的函数关系,化为顶点式即可得出答案;
②作FH⊥y轴于点H,得到AC∥PD∥FH∥x轴,易得,,易证得出,即,设,则,通过证得得出,代入即可得到n的值,进一步得到m的值.
(1)
∵△AOB是等边三角形,
∴∠AOB=60°,∴∠AOC=30°,
∵AC⊥y轴,点C的坐标为(0,),
∴OC=,
∴,
当△AOD是等腰三角形,OD=AD,∠DAO=∠DOA=30°,
∴∠CDA=60°,
∴,
∴,
∴D的坐标为,
当△AOD是等腰三角形,此时OA=OD时,,
∴OD=OA=2,
∴点D坐标为(0,2),
故答案为:或(0,2);
(2)
①解:设点D的坐标为(0,a),则OD=a,CD=-a,
∵△AOB是等边三角形,
∴,
∴,
在RtΔAOC中,,
∴,
∴,
∵,∴,
∵,∴,
∵,
∴,
∴,即:,
∴,
∴当时,m的最大值为;
∴m的最大值为时,点D坐标为;
②存在这样的m值,使BE=BF;
作FH⊥y轴于点H,
∴AC∥PD∥FH∥x轴,
∴,,
,
,
,,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
,
∵,,
∴,
∴,
∴,
解得: 或 ,
当时,点P与点A重合,不合题意,舍去,
当时, ,
存在这样的m值,使BE=BF.此时 .
【点睛】本题考查了等边三角形的性质、特殊角的三角函数,全等三角形的判定和性质、相似三角形的判定和性质以及二次函数的综合运用,解题的关键是得出二次函数的关系式,是对知识的综合考查.
13.(2022·山东烟台·中考真题)
(1)【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
(2)【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.
(3)【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且==.连接BD,CE.
①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
【答案】(1)见解析
(2)
(3)①;②
【分析】(1)证明△BAD≌△CAE,从而得出结论;
(2)证明△BAD∽△CAE,进而得出结果;
(3)①先证明△ABC∽△ADE,再证得△CAE∽△BAD,进而得出结果;
②在①的基础上得出∠ACE=∠ABD,进而∠BFC=∠BAC,进一步得出结果.
【详解】(1)证明:∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)解:∵△ABC和△ADE都是等腰直角三角形,
,∠DAE=∠BAC=45°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
;
(3)解:①,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,,
∴∠CAE=∠BAD,
∴△CAE∽△BAD,
;
②由①得:△CAE∽△BAD,
∴∠ACE=∠ABD,
∵∠AGC=∠BGF,
∴∠BFC=∠BAC,
∴sin∠BFC.
【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握“手拉手”模型及其变形.
14.(2022·吉林长春·中考真题)如图,在中,,,点M为边的中点,动点P从点A出发,沿折线以每秒个单位长度的速度向终点B运动,连结.作点A关于直线的对称点,连结、.设点P的运动时间为t秒.
(1)点D到边的距离为__________;
(2)用含t的代数式表示线段的长;
(3)连结,当线段最短时,求的面积;
(4)当M、、C三点共线时,直接写出t的值.
【答案】(1)3
(2)当0≤t≤1时,;当1<t≤2时,;
(3)
(4)或
【分析】(1)连接DM,根据等腰三角形的性质可得DM⊥AB,再由勾股定理,即可求解;
(2)分两种情况讨论:当0≤t≤1时,点P在AD边上;当1<t≤2时,点P在BD边上,即可求解;
(3)过点P作PE⊥DM于点E,根据题意可得点A的运动轨迹为以点M为圆心,AM长为半径的圆,可得到当点D、A′、M三点共线时,线段最短,此时点P在AD上,再证明△PDE∽△ADM,可得,从而得到,在中,由勾股定理可得,即可求解;
(4)分两种情况讨论:当点位于M、C之间时,此时点P在AD上;当点()位于C M的延长线上时,此时点P在BD上,即可求解.
(1)
解:如图,连接DM,
∵AB=4,,点M为边的中点,
∴AM=BM=2,DM⊥AB,
∴,
即点D到边的距离为3;
故答案为:3
(2)
解:根据题意得:当0≤t≤1时,点P在AD边上,
;
当1<t≤2时,点P在BD边上,;
综上所述,当0≤t≤1时,;当1<t≤2时,;
(3)
解:如图,过点P作PE⊥DM于点E,
∵作点A关于直线的对称点,
∴A′M=AM=2,
∴点A的运动轨迹为以点M为圆心,AM长为半径的圆,
∴当点D、A′、M三点共线时,线段最短,此时点P在AD上,
∴,
根据题意得:,,
由(1)得:DM⊥AB,
∵PE⊥DM,
∴PE∥AB,
∴△PDE∽△ADM,
∴,
∴,
解得:,
∴,
在中,,
∴,解得:,
∴,
∴;
(4)
解:如图,
当点M、、C三点共线时,且点位于M、C之间时,此时点P在AD上,
连接A A′, A′B,过点P作PF⊥AB于点F,过点A′作A′G⊥AB于点G,则A A′⊥PM,
∵AB为直径,
∴∠A =90°,即A A′⊥A′B,
∴PM∥A′B,
∴∠PMF=∠AB A′,
过点C作CN⊥AB交AB延长线于点N,
在中,AB∥DC,
∵DM⊥AB,
∴DM∥CN,
∴四边形CDMN为平行四边形,
∴CN=DM=3,MN=CD=4,
∴CM=5,
∴,
∵ M=2,
∴,
∴,
∴,
∴,
∴,
∴,即PF=3FM,
∵,,
∴,
∴,即AF=2FM,
∵AM=2,
∴,
∴,解得:;
如图,当点()位于C M的延长线上时,此时点P在BD上,,
过点作于点G′,则,取的中点H,则点M、P、H三点共线,过点H作HK⊥AB 于点K,过点P作PT⊥AB于点T,
同理:,
∵HK⊥AB,,
∴HK∥A′′G′,
∴,
∵点H是的中点,
∴,
∴,
∴,
∴,
∴,即MT=3PT,
∵,,
∴,
∴,
∵MT+BT=BM=2,
∴,
∴,解得:;
综上所述,t的值为或.
【点睛】本题主要考查了四边形的综合题,熟练掌握平行四边形的性质,圆的基本性质,相似三角形的判定和性质,解直角三角形,根据题意得到点的运动轨迹是解题的关键,是中考的压轴题.
15.(2022·内蒙古通辽·中考真题)已知点在正方形的对角线上,正方形与正方形有公共点.
(1)如图1,当点在上,在上,求的值为多少;
(2)将正方形绕点逆时针方向旋转,如图2,求:的值为多少;
(3),,将正方形绕逆时针方向旋转,当,,三点共线时,请直接写出的长度.
【答案】(1)2
(2)
(3)或
【分析】(1)根据题意可得,根据平行线分线段成比例即可求解;
(2)根据(1)的结论,可得,根据旋转的性质可得,进而证明,根据相似三角形的性质即可求解;
(3)分两种情况画出图形,证明△ADG∽△ACE,根据相似三角形的判定和性质以及勾股定理即可得出答案.
(1)
解:正方形与正方形有公共点,点在上,在上,
四边形是正方形
(2)
解:如图,连接,
正方形绕点逆时针方向旋转,
,
(3)
解:①如图,
,,
,,,
三点共线,
中,,
,
由(2)可知,
,
.
②如图:
由(2)知△ADG∽△ACE,
∴,
∴DG=CE,
∵四边形ABCD是正方形,
∴AD=BC=8,AC=,
∵AG=AD,
∴AG=AD=8,
∵四边形AFEG是正方形,
∴∠AGE=90°,GE=AG=8,
∵C,G,E三点共线.
∴∠AGC=90°
∴CG=,
∴CE=CG+EG=8+8,
∴DG=CE=.
综上,当C,G,E三点共线时,DG的长度为或.
【点睛】本题考查了平行线分线段成比例,相似三角形的性质与判定,正方形的性质,勾股定理,旋转的性质,综合运用以上知识是解题的关键.
16.(2022·湖南郴州·中考真题)如图1,在矩形ABCD中,,.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作,交AB于点F.
(1)求证:;
(2)如图2,连接CF,过点B作,垂足为G,连接AG.点M是线段BC的中点,连接GM.
①求的最小值;
②当取最小值时,求线段DE的长.
【答案】(1)见解析
(2)①5;②或
【分析】(1)证明出即可求解;
(2)①连接AM.先证明.确定出点G在以点M为圆心,3为半径的圆上.当A,G,M三点共线时,.此时,取最小值.在中利用勾股定理即可求出AM,则问题得解.②先求出AF,求AF的第一种方法:过点M作交FC于点N,即有,进而有.设,则,.再根据,得到,得到,则有,解方程即可求出AF;求AF的第二种方法:过点G作交BC于点H.即有.则有,根据,可得,进而求出,.由得,即可求出AF.求出AF之后,由(1)的结论可得.设,则,即有,解得解方程即可求出DE.
(1)
证明:如图1,
∵四边形ABCD是矩形,
∴,
∴.
∵,
∴,
∴,
∴;
(2)
①解:如图2-1,连接AM.
∵,
∴是直角二角形.
∴.
∴点G在以点M为圆心,3为半径的圆上.
当A,G,M三点不共线时,由三角形两边之和大于箒三边得:,
当A,G,M三点共线时,.
此时,取最小值.在中,.
∴的最小值为5.
②(求AF的方法一)如图2-2,过点M作交FC于点N,
∴.
∴.
设,则,
∴.
∵,
∴,
∴,
由①知的最小值为5、即,
又∵,
∴.
∴,解得,即.
(求AF的方法二)
如图2-3,过点G作交BC于点H.
∴.
∴,
由①知的最小值为5,即,
又∵,
∴.
∴,.
由得,
∴,即,
解得.
∴.
由(1)的结论可得.
设,则,
∴,
解得或.
∵,,
∴或.
【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识,掌握相似三角形的判定与性质是解答本题的关键.
17.(2022·广西贵港·中考真题)已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧,,与相交于点O.
(1)如图1,若连接,则的形状为______,的值为______;
(2)若将沿直线l平移,并以为一边在直线l的上方作等边.
①如图2,当与重合时,连接,若,求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
【答案】(1)等腰三角形,
(2)①;②见解析
【分析】(1)过点C作CH⊥BD于H,可得四边形ABHC是矩形,即可求得AC=BH,进而可判断△BCD的形状,AC、BD都垂直于l,可得△AOC∽△BOD,根据三角形相似的性质即可求解.
(2)①过点E作于点H,AC,BD均是直线l的垂线段,可得,根据等边三角形的性质可得,再利用勾股定理即可求解.
②连接,根据,得,即是等边三角形,把旋转得,根据30°角所对的直角边等于斜边的一般得到,则可得,根据三角形相似的性质即可求证结论.
(1)
解:过点C作CH⊥BD于H,如图所示:
∵AC⊥l,DB⊥l,CH⊥BD,
∴∠CAB=∠ABD=∠CHB=90°,
∴四边形ABHC是矩形,
∴AC=BH,
又∵BD=2AC,
∴AC=BH=DH,且CH⊥BD,
∴的形状为等腰三角形,
∵AC、BD都垂直于l,
∴,
∴△AOC∽△BOD,
,即,
,
故答案为:等腰三角形,.
(2)
①过点E作于点H,如图所示:
∵AC,BD均是直线l的垂线段,
∴,
∵是等边三角形,且与重合,
∴∠EAD=60°,
∴,
∴,
∴在中,,,
又∵,,
∴,
∴,AE=6
在中,,
又由(1)知,
∴,则,
∴在中,由勾股定理得:.
②连接,如图3所示:
∵,
∴,
∵由(1)知是等腰三角形,
∴是等边三角形,
又∵是等边三角形,
∴绕点D顺时针旋转后与重合,
∴,
又∵,
∴,
∴,
∴,
又,
∴,
∴,
∴.
【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用,熟练掌握三角形相似的判定及性质和勾股定理的应用,巧妙借助辅助线是解题的关键.
18.(2022·山东青岛·中考真题)如图,在中,,将绕点A按逆时针方向旋转得到,连接.点P从点B出发,沿方向匀速运动,速度为;同时,点Q从点A出发,沿方向匀速运动,速度为.交于点F,连接.设运动时间为.解答下列问题:
(1)当时,求t的值;
(2)设四边形的面积为,求S与t之间的函数关系式;
(3)是否存在某一时刻t,使?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)
(2)
(3)存在,
【分析】(1)利用得,即,进而求解;
(2)分别过点C,P作,垂足分别为M,N,证得,,求得,再证得,得出,根据即可求出表达式;
(3)当时,易证,得出,则,进而求出t值.
(1)
解:在中,由勾股定理得,
∵绕点A按逆时针方向旋转得到
∴
∵
∴
又
∴
∴
∴
∴
答:当时,t的值为.
(2)
解:分别过点C,P作,垂足分别为M,N
∵
∴
又
∴
∴
∴
∴
∵
∴
∴
∴
∴
∴
∴
∴
(3)
解:假设存在某一时刻t,使
∵
∴
∵
∴
又
∴
∴
∴
∴
∴存在时刻,使.
【点睛】本题考查了旋转与相似,利用勾股定理求线段长,平行线的性质,根据旋转的性质,找到相似图形是解决问题的关键,是中考中的常考题.
19.(2022·辽宁营口·中考真题)在平面直角坐标系中,抛物线经过点和点,与y轴交于点C,点P为抛物线上一动点.
(1)求抛物线和直线的解析式;
(2)如图,点P为第一象限内抛物线上的点,过点P作,垂足为D,作轴,垂足为E,交于点F,设的面积为,的面积为,当时,求点P坐标;
(3)点N为抛物线对称轴上的动点,是否存在点N,使得直线垂直平分线段?若存在,请直接写出点N坐标,若不存在,请说明理由.
【答案】(1)抛物线解析式为,直线的解析式为,
(2)
(3)存在
【分析】(1)待定系数法求解析式即可求解;
(2)设,则,中,,证明,根据相似三角形的性质以及建立方程,解方程即可求解;
(3)设直线交轴于点,设交于点,连接,,,证明是等腰直角三角形,则设,则,,根据列出方程,即可求解.
(1)
解:抛物线经过点和点,
,
解得,
抛物线解析式为,
设直线的解析式为,
,
解得,
直线的解析式为,
(2)
如图,设直线与轴交于点,
由,令,得,则,
,
,
设,则,
,
,
,
,
,
,
中,,
设的面积为,的面积为,
,
,
,
即,
设,则,
,
解得或(舍),
当时, ,
(3)
设直线交轴于点,设交于点,连接,,,如图,
由,令,得,则
设过直线的解析式为,
解得
过直线的解析式为,
是等腰直角三角形
是等腰直角三角形
直线垂直平分线段
是等腰直角三角形,
,
设,则,
,
解得(舍)
即
【点睛】本题考查了二次函数综合,解直角三角形,相似三角形的性质与判定,二次函数线段问题,掌握以上知识是解题的关键.
20.(2022·山东威海·中考真题)回顾:用数学的思维思考
(1)如图1,在△ABC中,AB=AC.
①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)猜想:用数学的眼光观察
经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
(3)探究:用数学的语言表达
如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
【答案】(1)见解析
(2)添加条件CD=BE,见解析
(3)能,0<CF<
【分析】(1)①利用ASA证明△ABD≌△ACE.
②利用SAS证明△ABD≌△ACE.
(2)添加条件CD=BE,证明AC+CD=AB+BE,从而利用SAS证明△ABD≌△ACE.
(3)在AC上取一点D,使得BD=CE,根据BF=CE,得到BD=BF,当BD=BF=BA时,可证△CBF∽△BAF,运用相似性质,求得CF的长即可.
(1)
①如图1,∵AB=AC,
∴∠ABC=∠ACB,
∵BD,CE是△ABC的角平分线,
∴∠ABD=∠ABC,∠ACE =∠ACB,
∴∠ABD=∠ACE,
∵AB=AC,∠A=∠A,
∴△ABD≌△ACE,
∴BD=CE.
②如图1,∵AB=AC,点D,E分别是边AC,AB的中点,
∴AE=AD,
∵AB=AC,∠A=∠A,
∴△ABD≌△ACE,
∴BD=CE.
(2)
添加条件CD=BE,证明如下:
∵AB=AC,CD=BE,
∴AC+CD=AB+BE,
∴AD=AE,
∵AB=AC,∠A=∠A,
∴△ABD≌△ACE,
∴BD=CE.
(3)
能
在AC上取一点D,使得BD=CE,根据BF=CE,得到BD=BF,
当BD=BF=BA时,E与A重合,
∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,∠A=∠BFA=36°,
∴∠ABF=∠BCF=108°,∠BFC=∠AFB,
∴△CBF∽△BAF,
∴,
∵AB=AC=2=BF, 设CF=x,
∴,
整理,得,
解得x=,x=(舍去),
故CF= x=,
∴0<CF<.
【点睛】本题考查了等腰三角形的性质,三角形全等的判定和性质,三角形相似的判定和性质,一元二次方程的解法,熟练掌握等腰三角形的性质,三角形全等的判定,三角形相似的判定性质是解题的关键.
相关试卷
这是一份中考数学二轮复习压轴题培优训练专题24以三角形为载体的几何综合问题(2份,原卷版+解析版),文件包含中考数学二轮复习压轴题培优训练专题24以三角形为载体的几何综合问题原卷版doc、中考数学二轮复习压轴题培优训练专题24以三角形为载体的几何综合问题解析版doc等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。
这是一份专题27以相似为载体的几何综合问题(教师版)-拔尖2023中考数学压轴题突破(全国通用),共70页。试卷主要包含了,连接DG等内容,欢迎下载使用。
这是一份专题27以相似为载体的几何综合问题-(学生版)-拔尖2023中考数学压轴题突破(全国通用),共12页。








