陕西省西安市西咸新区秦汉中学2023-2024学年九年级上学期月考数学试题（原卷版）-A4

这是一份陕西省西安市西咸新区秦汉中学2023-2024学年九年级上学期月考数学试题（原卷版）-A4，共6页。试卷主要包含了请将答案正确填写在答题纸上等内容，欢迎下载使用。
说明：
1．本卷共24道题，满分120分，考试时长120分钟；
2．请将答案正确填写在答题纸上。
第一部分(选择题 共 24分)
一． 选择题(共8小题，每小题3分，共24分)
1. 下列函数中， 是二次函数的是( )
A. B. C. D.
2. 在中，，，则（ ）
A. B. C. D.
3. 在平面直角坐标系中，将抛物线先向右平移2个单位，再向上平移2个单位，得到的抛物线的解析式是（ ）
A. B. C. D.
4. 已知0≤x≤，那么函数y=﹣2x2+8x﹣6的最大值是（ ）
A. ﹣10.5B. 2C. ﹣2.5D. ﹣6
5. 若点都在反比例函数的图象上，则a，b，c的大小关系用“＜”连接的结果为（ ）
A. B. C. D.
6. 如图，在同一坐标系中，二次函数与一次函数的图象大致是（ ）
A. B. C. D.
7. 若图中反比例函数的表达式均为，则阴影部分面积为2的是（ ）
A. B. C. D.
8. 如图，抛物线的对称轴是直线． 且过点，有下列结论：①；②；③；④；⑤；其中所有正确的结论是（ ）
A. ①②④B. ②③④C. ①③④D. ①③⑤
二． 填空题(共5小题)
9. 已知函数是反比例函数，则______．
10. 如果三点，和在抛物线的图象上，那，，之间的大小关系是______ ．
11. 如图，河堤的横断面迎水坡的坡比是，堤高，则坡面的长度是___________．

12. 抛物线向右平移2个单位长度，再向上平移3个单位长度，得到抛物线的顶点坐标是______．
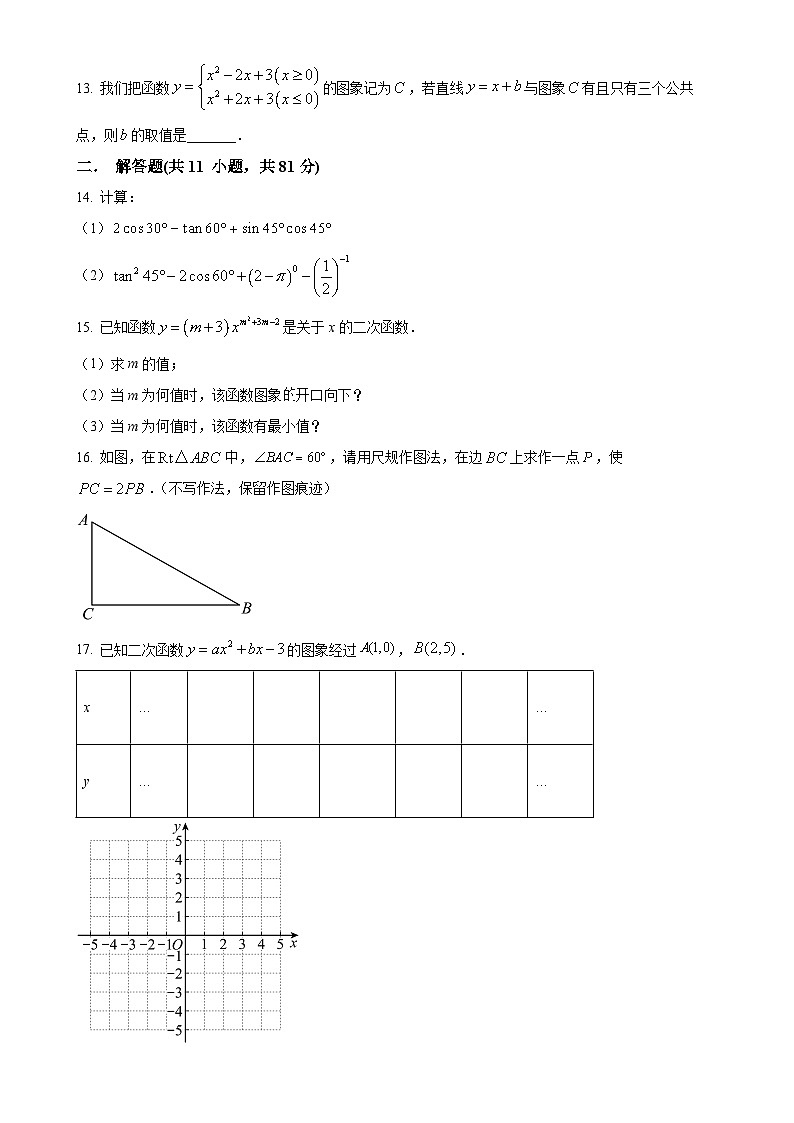
13. 我们把函数图象记为，若直线与图象有且只有三个公共点，则的取值是_______．
二． 解答题(共11 小题，共81分)
14. 计算：
（1）
（2）
15. 已知函数是关于x的二次函数．
（1）求m的值；
（2）当m为何值时，该函数图象开口向下？
（3）当m为何值时，该函数有最小值？
16. 如图，在中，，请用尺规作图法，在边上求作一点，使．（不写作法，保留作图痕迹）

17. 已知二次函数的图象经过，．
（1）求此二次函数表达式；
（2）求该函数图象的顶点坐标；
（3）画出该函数图象；
（4）结合图象，直接写出当时，y取值范围．
18. 如图， 在中，，点D在边上，若，求的值．
19. 已知抛物线L：过点和，与x轴的交点为A，B(点A在点B的左侧)，与y轴交于点C．
（1）求抛物线L的表达式；
（2）抛物线与L关于原点对称，求出表达式；
（3）点P在抛物线上，，的是A，B的对称点，若与的面积相等，求点P的坐标．
20. 某景区、两个景点位于湖泊两侧，游客从景点到景点必须经过处才能到达．观测得景点在景点的北偏东30°，从景点出发向正北方向步行到达处，测得景点在的北偏东75°方向，当地政府为了便捷游客游览，打算修建一条从景点到景点的笔直的跨湖大桥，求跨湖大桥的长度．（结果保留根号）

21. 已知，当时，函数的最小值为，求的值．
22. 如图，在平面直角坐标系中，二次函数的图像与轴交于，两点，与轴交于点，且．

（1）求直线的表达式；
（2）求该二次函数的解析式，并写出函数值随的增大而减小时的取值范围；
（3）点是抛物线上的一个动点，设点的横坐标为．当的面积取最大值时，求点的坐标．
23. 如图，已知抛物线与x轴交于A，B两点，与y轴交于C点，顶点为D，其中，．直线经过B，C两点．

（1）求直线和抛物线的解析式；
（2）在抛物线对称轴上找一点M，使最小，直接写出点M的坐标；
（3）连接，求的面积．
24. 我们不妨约定：在平面直角坐标系中，横、纵坐标互为倒数的点为“倒数点”.
（1）若点是“倒数点”，则_______；
（2）若一次函数图象上有两个“倒数点、，若的面积为，求的值；
（3）如图，已知顶点为的二次函数与轴交于、两点，且，交轴于点，过、两点的直线交轴于点，满足；
①求的值；
x
…
…
y
…
…