人教版（2024）八年级下册17.1 勾股定理精品教学课件ppt

这是一份人教版（2024）八年级下册17.1 勾股定理精品教学课件ppt，文件包含1712勾股定理pptx、1712《勾股定理》教学设计docx、《17章勾股定理》单元整体教学doc等3份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
1.会运用勾股定理求线段长及解决简单的实际问题.2.能从实际问题中抽象出直角三角形这一几何模型，利用勾股定理建立已知边与未知边长度之间的联系，并进一步求出未知边长.
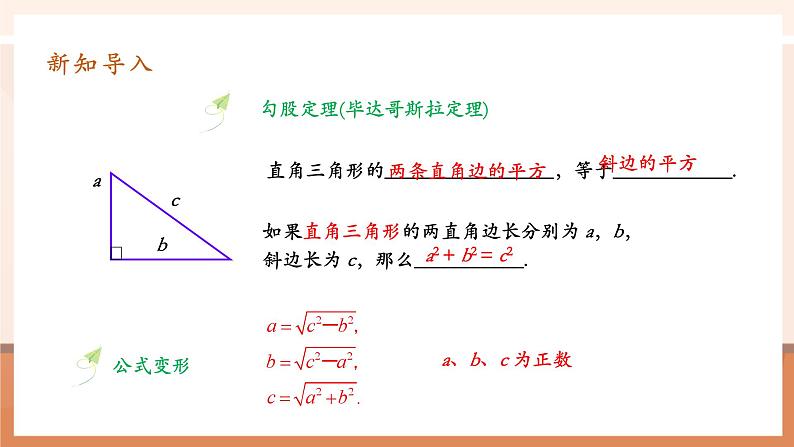
直角三角形的_________________，等于____________.
如果直角三角形的两直角边长分别为 a，b，斜边长为 c，那么___________.
a2 + b2 = c2
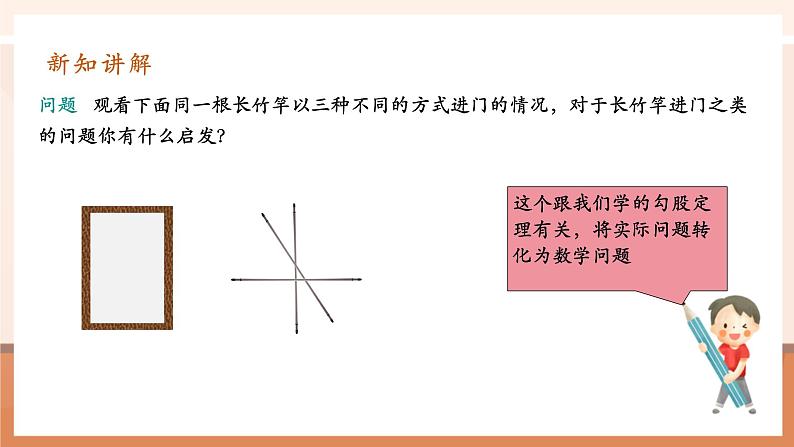
问题 观看下面同一根长竹竿以三种不同的方式进门的情况，对于长竹竿进门之类的问题你有什么启发？
这个跟我们学的勾股定理有关，将实际问题转化为数学问题
例1.一个门框的尺寸如图所示，一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
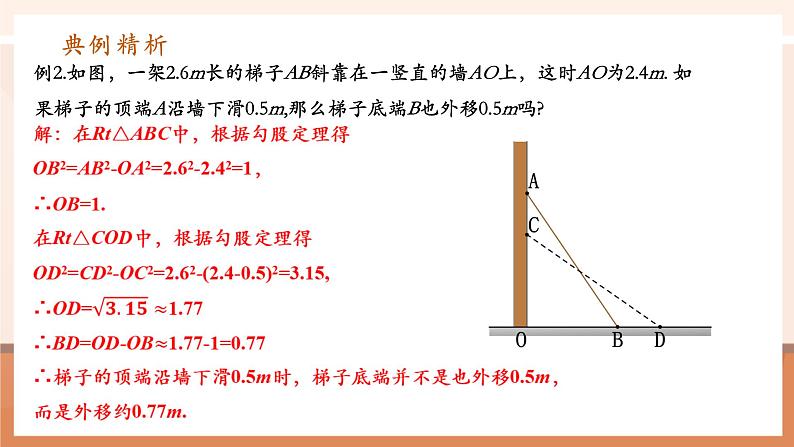
例2.如图，一架2.6m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
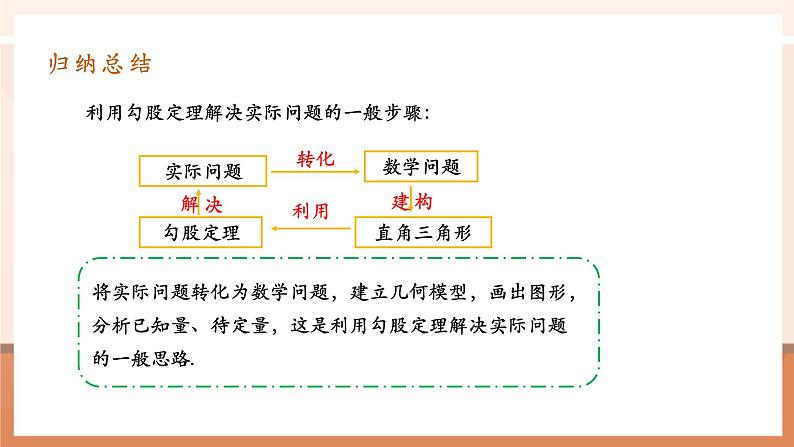
利用勾股定理解决实际问题的一般步骤：
将实际问题转化为数学问题，建立几何模型，画出图形，分析已知量、待定量，这是利用勾股定理解决实际问题的一般思路.
【知识技能类作业】必做题：
【知识技能类作业】选做题：
5．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一根到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( )A．12≤a≤13 B．12≤a≤15C．5≤a≤12 D．5≤a≤13
6．情景应用一辆卡车装满货物后，高为2.88 m，宽为1.88 m，请判断 该卡车能否通过如图所示的工厂厂门(上方为半圆)？说明你的理由.
用勾股定理解决实际问题
1．一架5 m长的梯子斜靠在建筑物上，如果梯子的底端离建筑物3 m 远，那么该梯子可以达到建筑物的高度是(　C　) A．2 m B．3 m C．4 m D．5 m2.小强量得家里新购置的液晶电视屏幕的长为93 cm，宽为52 cm，这台液晶电视的尺寸(屏幕的对角线长度为电视机的尺寸)最有可能是(　　)英寸(约81 cm) B.50英寸(127 cm)C.42英寸(约107 cm) D.60英寸(约152 cm)
3．如图是某地的长方形大理石广场示意图，如果小王从A角走到C 角，那么至少走 米．4．如图，根据图形中已知条件，可求得阴影部分(半圆)的面积是 cm2．
5．在平静的湖面上，有一枝红莲，高出水面1 m，一阵风吹来，红莲吹到一边，花朵齐及水面，已知红莲移动的水平距离为2 m，则这里的水深是多少？
解：设水深OC为x m，则OB＝(x＋1) m，由勾股定理，得22＋x2＝(x＋1)2，得2x＝3，∴x＝1.5，∴这里的水深是1.5 m
6．八年级11班松松同学学习了“勾股定理”之后，为了测量如图的 风筝的高度CE，测得如下数据：①测得BD的长度为8米；(注：BD⊥CE)②根据手中剩余线的长度计算出风筝线BC的长为17米；③牵线放风筝的松松身高1.6米．(1)求风筝的高度CE；(2)若松松同学想让风筝沿CD方向下降9米，则他应该往回收线多 少米？
答：风筝的高度CE为16.6米．