人教版（2024）八年级下册19.1.2 函数的图象精品教学课件ppt

这是一份人教版（2024）八年级下册19.1.2 函数的图象精品教学课件ppt，文件包含19122函数的图象pptx、《19122函数的图象》教学设计docx、《19章一次函数》单元教学doc等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
1.了解函数的三种表示方法及其优缺点；2.能用适当的方式表示简单实际问题中的变量之间的函数关系；3.能对函数关系进行分析，对变量的变化情况进行初步讨论.
1.函数的图象： 一般的，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.
2.函数图象的画法步骤
通过前面的学习，我们都可以用什么方法表示一些函数？
写出函数解析式，或者列表格，或者画函数图象，都可以表示具体的函数.这三种表示函数的方法，分别称为解析法、列表法和图象法.
y = x + 0.5
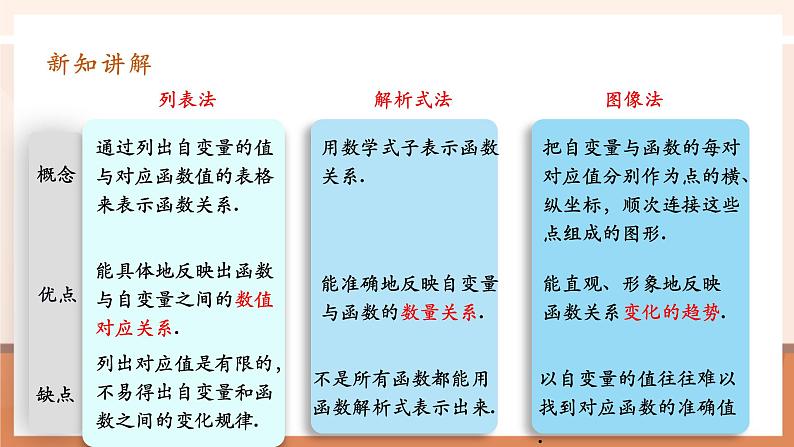
通过列出自变量的值与对应函数值的表格来表示函数关系.
能具体地反映出函数与自变量之间的数值对应关系.
列出对应值是有限的，不易得出自变量和函数之间的变化规律.
用数学式子表示函数关系.
能准确地反映自变量与函数的数量关系.
把自变量与函数的每对对应值分别作为点的横、纵坐标，顺次连接这些点组成的图形.
能直观、形象地反映函数关系变化的趋势.
不是所有函数都能用函数解析式表示出来.
以自变量的值往往难以找到对应函数的准确值.
例1.一水库的水位在最近5 h 内持续上涨，下表记录了这5 h 内6 个时间点的水位高度，其中 t 表示时间，y表示水位高度．　 （1）在平面直角坐标系中描出表中数据对应的点，这些点是否在一条直线上？由此你发现水位变化有什么规律？(2)水位高度 y 是否为时间 t 的函数？如果是，试写出一个符合表中数据的函数解析式，并画出这个函数的图象.这个函数能表示水位的变化规律吗？(3)据估计这种上涨规律还会持续2h，预测再过2h水位高度将为多少米.
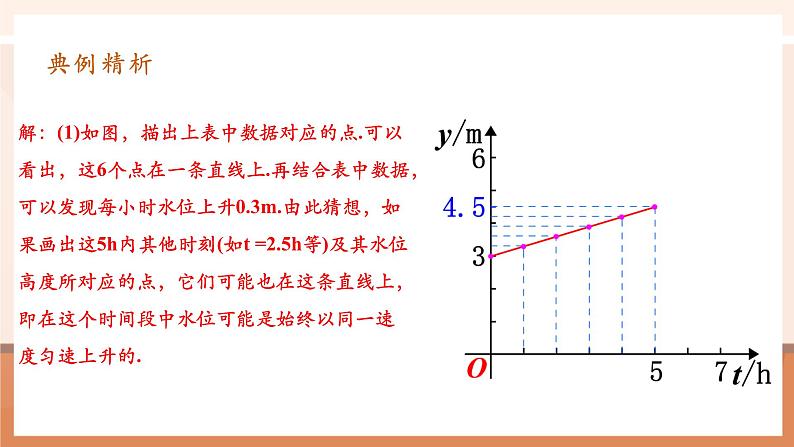
解：(1)如图，描出上表中数据对应的点.可以看出，这6个点在一条直线上.再结合表中数据，可以发现每小时水位上升0.3m.由此猜想，如果画出这5h内其他时刻(如t =2.5h等)及其水位高度所对应的点，它们可能也在这条直线上，即在这个时间段中水位可能是始终以同一速度匀速上升的.
(2)由于水位在最近5h内持续上涨，对于时间 t 的每一个确定的值，水位高度 y 都有唯一的值与其对应，所以 y 是 t 的函数.开始时水位高度为3m，以后每小时水位上升0.3m.函数y=0.3t+3 (0≤t≤5)是符合表中数据的一个函数，它表示经过 t h水位上升0.3t m，即水位y为(0.3t+3)m，其图象是右图中点A(0，3)和点B(5，4.5)之间的线段AB. 如果在这5h内，水位一直匀速上升，即升速为0.3m/h，那么函数y=0.3t+3 (0≤t≤5)就精确地表示了这种变化规律.即使在这5h内，水位的升速有些变化，而由于每小时水位上升0.3是确定的，因此这个函数可以近似地表示水位的变化规律.
(3)如果水位的变化规律不变，则可利用函数 y=0.3t +3 预测，再过2h，即t =5+2=7(h)时，水位高度 y =0.3×7+3=5.1(m)或把右图中的函数图象(线段AB)向右延伸到t =7所对应的位置，也能看出这时的水位高度约为5.1m.
【知识技能类作业】必做题：
A. B. C. D.
【知识技能类作业】选做题：
5.已知动点P以2cm/s的速度沿如图①所示的边框按B→C→D→E→F→A的路径匀速移动，相应的△ABP的面积S（单位：cm2）关于时间t（单位：s）的函数图象如图②所示.若AB=6 cm，试回答下列问题：（1）求出图①中BC的长和多边形ABCDEF的面积；（2）求出图②中a和b的值.
一目了然，对表格中已有自变量的每一个值，可直接找到与它对应的函数值.
直观、形象地反映出函数关系的变化趋势和某些性质.
能明显地表示自变量与函数的对应关系.
列表法、解析式法、图象法
1.小明因感冒发烧住院治疗，护士为了较直观地反映小明某天24小时的体温与时间的关系，比较好的方式是应该选择( )A.列表法 B.图象法 C.解析法 D.三种方法都可以2.在某次实验中，测得两个变量m和v之间的4组对应数据如下表，则m与v之间的关系最接近于下列各关系式中的( )A. v=2m-2 B. v=m2-1 C. v=3m-3 D. v=m+1
3．农用机械的油箱装油56千克，工作时平均每小时耗油6千克，则油箱中剩油量q(千克)与时间t(小时)之间的关系式是_________________，自变量的取值范围是___________________．4．某水库的水位在6 h内持续上涨，初始的水位高度为8 m，水位以0.2 m/h的速度匀速上升，则水库的水位高度y(m)与时间x(h)之间的函数解析式为_________________________．
y＝8＋0.2x(0≤x≤6)
5．某市居民用水实行阶梯收费，每户每月的用水量如果未超过20吨，按每吨2.5元收费；如果超过20吨，未超过的部分仍按每吨2.5元收费，超过的部分按每吨3.3元收费．设某户每月的用水量为x吨，应缴水费为y元．(1)请写出y与x之间的函数关系式；(2)若该市某户4月份的水费平均为每吨2.8元，则该户4月份用水多少吨？
(2) ∵2.8＞2.5，∴该户4月份用水超过20吨．设该户4月份用水a吨，则2.8a＝3.3a－16，解得a＝32，∴该户4月份用水32吨