八年级下册19.3 课题学习 选择方案优质课教学课件ppt

这是一份八年级下册19.3 课题学习 选择方案优质课教学课件ppt，文件包含193课题学习选择方案pptx、《193课题学习选择方案》教学设计docx、《19章一次函数》单元教学doc等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。
1．会用一次函数知识解决方案选择问题，体会函数模型思想；2．能从不同的角度思考问题，优化解决问题的方法；3．能进行解决问题过程的反思，总结解决问题的方法．
生活中遇到这样的问题该如何选择呢？
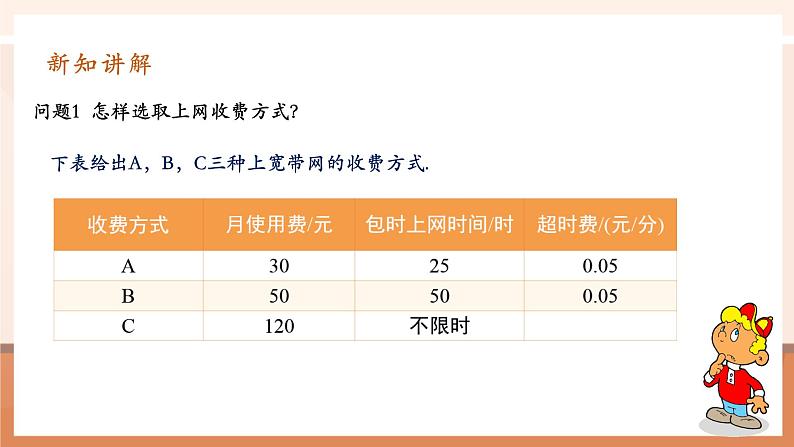
问题1 怎样选取上网收费方式？
下表给出A，B，C三种上宽带网的收费方式.
1.哪种方式上网费是会变化的，在A、B两种方式中，上网费由哪些部分组成？2.什么影响了上网费用，这三种方式中有一定最优惠的方式吗？
A、B两种方式上网费=月使用费+超时费
上网时间影响了上网费用，没有一定最优惠的方式
设月上网时间为 x h，方案A，B，C的收费金额分别为y1，y2，y3，写出它们的函数解析式.
y3=120 (x≥0)
当上网时__________ 时，选择方式A最省钱.
当上网时间__________ 时，选择方式B最省钱.
当上网时间________ _时，选择方式C最省钱.
在同一坐标系画出它们的图象：
答：当上网时间不超过31小时40分,选择方案A最省钱;当上网时间为31小时40分至73小时20分,选择方案B最省钱当上网时间超过73小时20分,选择方案C最省钱.
解决含有多个变量的问题时，可以分析这些变量之间的关系，从中选取一个取值能影响其他变量的值的变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数，以此作为解决问题的数学模型.
问题2. 怎样租车？某学校计划在总费用2300元限额内，租用汽车送234名学生和6名教师集体外出活动，每辆汽车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如下表所示.
(1)共需租多少辆汽车？(2)给出最节省费用的租车方案.
解：(1)要保证240名师生都有车坐，汽车总数不能小于6辆；要使每辆汽上至少要有1名教师，汽车总数不能大于6辆. 综合起来可知汽车总数为6辆.
(2)设租用x辆甲种客车，则租车费用y(单位：元)是x的函数，即 y=400x+280(6-x)  化简为：y=120x+1680  
方案一：当x=4时，即租用4辆甲种汽车，2辆乙种汽车. 租车费用y=120×4+1680=2160(元)方案二：当x=5时，即租用5辆甲种汽车，1辆乙种汽车. 租车费用y=120×5+1680=2280(元)因此，为节省费用应选择方案一.
还有其它选择方案的方法吗？
∵120>0，∴y随着x的增大而增大,∴当x=4时,y最小,y的最小值为：120×4+1680=2160．
答：租用4辆甲种客车,租用2辆乙种客车时租车费用最少，最少租车费用为2160元.
上网多少分钟费用相等：y1=y2;怎样租车最省钱：x取什么值时y最小？
【知识技能类作业】必做题：
1. 某市体育馆将举办明星足球赛，为此体育馆推出两种团体购票方案(设购票张数为x张，购票总价为y元). 方案一：购票总价由图中的折线OAB所表示的函数关系确定；方案二：提供8 000元赞助后，每张票的票价为50元. 则两种方案购票总价相同时，x的值为(　　)A. 80 B. 120 C. 160 D. 200
2.如图，某通信公司提供了A，B两种方案的通信费用y(单位：元)与通话时间x(单位：min)之间的关系图，则下列说法错误的是(　　).
A.若通话时间少于120 min，则方案A比方案B便宜20元B.若通话时间超过200 min，则方案B比方案A便宜12元C.若两种方案通信费用相差10元，则通话时间是145 min或185 minD.若通信费用为60元，则方案B比方案A的通话时间多
【知识技能类作业】选做题：
3.某旅行团有10名成人和x名儿童，他们准备去北京旅游，甲旅行社说：“若成人买全票，儿童全部半价优惠.”乙旅行社说：“所有人按全票价的六折优惠.”已知全票价为2 400元.设甲旅行社的收费为y甲元，乙旅行社的收费为y乙元，则两家旅行社的收费关于儿童人数x的函数解析式分别为_______________________________________________________________.4.某公司因业务发展需要，准备与汽车租赁公司签订租车合同.甲租赁公司的收费标准是每千米收1元租车费，另收3 000元月租；乙租赁公司的收费标准是每千米收 4 元租车费，不收月租.该公司计划花费5 000元用于汽车租赁，选择________(填“甲”或“乙”)汽车租赁公司比较合算. 
y甲＝1 200x＋24 000，y乙＝1 440x＋14 400　
5.某商店出售普通练习本和精装练习本，150本普通练习本和100精装练习本销售总额为1 450元；200本普通练习本和50精装练习本销售总额为1 100元. (1)求普通练习本和精装练习本的销售单价分别是多少？
(2)该商店计划再次购进500本练习本，普通练习本的数量不低于精装练习本数量的3倍，已知普通练习本的进价为2元/个，精装练习本的进价为7元/个，设购买普通练习本x个，获得的利润为W元；①求W关于x的函数解析式；解：①设购买普通练习本x个，则购买精装练习本(500－x)个. 由题意，得W＝(3－2)x＋(10－7)(500－x)＝－2x＋1 500. ∵普通练习本的数量不低于精装练习本数量的3倍，∴x≥3(500－x)，解得x≥375. ∴W关于x的函数解析式是W＝－2x＋1 500(375≤x≤500).
②该商店应如何进货才能使销售总利润最大？并求出最大利润. 解：②∵W＝－2x＋1 500，∴W随x的增大而减小，∵375≤x≤500，∴当x＝375时，W取得最大值，此时W＝750，500－x＝125. 答：当购买375个普通练习本，125个精装练习，销售总利润最大，最大总利润为750元.
用一次函数解决实际问题的方法与策略
一、怎样选取上网收费方式
1.某单位需要用车，准备和一个体车主或一国有出租车公司其中的一家签订合同.设汽车每月行驶xkm，应付给个体车主的月租费是y1元，付给出租车公司的月租费是y2元，y1，y2分别与x之间的函数关系图象是如下图的两条直线.观察图象,回答下列问题:(1)每月行驶的路程等于_____km时，租两家出租车的费用相同; (2)每月行驶的路程x_______时，y1租个体车主的出租车合算;(3)如果这个单位估计每月行驶的路程为1300km，那么这个单位租______________ 的出租车合算.
2．如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x（件）之间的函数图象．下列说法, 其中正确的说法有             ．（填序号） ①售2件时甲、乙两家售价一样； ②买1件时买乙家的合算； ③买3件时买甲家的合算； ④买1件时，售价约为3元.
3．某通信公司就手机流量套餐推出三种方案，如下表：
A，B，C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示．
(1)填空：m＝ _______，n＝ ______；(2)在A方案中，当每月使用的流量不少于1024兆时，则每月所需的费用y(元)与每月使用的流量x(兆)之间的函数解析式为 __________________________；(写出自变量的取值范围)(3)在这三种方案中，当每月使用的流量超过多少兆时，选择C方案最划算？
y＝0.3x－287.2(x≥1024)
解：(3)3072＋(266－56)÷0.3＝3772(兆)，由图象得，当每月使用的流量超过3772兆时，选择C方案最划算
4.某校实行学案式教学，需印制若干份数学学案.印刷厂有甲、乙两种收费方式，除按份数收取印刷费外，甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:(1)填空:甲种收费方式的解析式为_____________，乙种收费方式的函数解析式为___________;(2)该校某年级每次需印制100~450 (含100和450)份学案，选择哪种印制方式较合算?
解: (2)由0.1x+6>0.12x，得x