中职数学苏教版（中职）第一册第5章 三角函数评课课件ppt

这是一份中职数学苏教版（中职）第一册第5章 三角函数评课课件ppt，共40页。PPT课件主要包含了角的概念，象限角，弧度制，半径长，任意角的三角函数，sinα，cosα，tanα，象限角与轴线角，同角三角函数关系等内容，欢迎下载使用。
第四章三角函数与解三角形
1.定义：角可以看成一条射线绕着它的　　　旋转所成的图形.2.分类
按旋转方向不同分为　　　、　　　、　　　.按终边位置不同分为　　　　和轴线角.
3.相反角：我们把射线OA绕端点O按不同方向旋转　　　的量所成的两个角叫做互为相反角.角α的相反角记为　　　.4.终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S＝　　　　　　　　　　　　.
{β|β＝α＋k·360°，k∈Z}
1.定义：把长度等于　　　　的圆弧所对的圆心角叫做1弧度的角，弧度单位用符号rad表示.
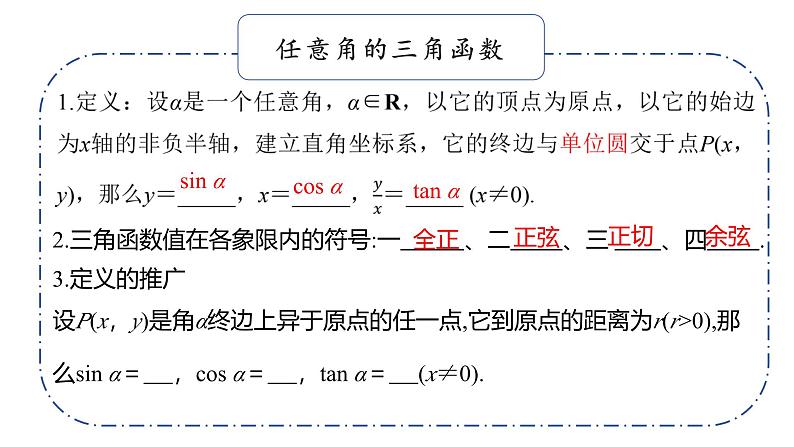
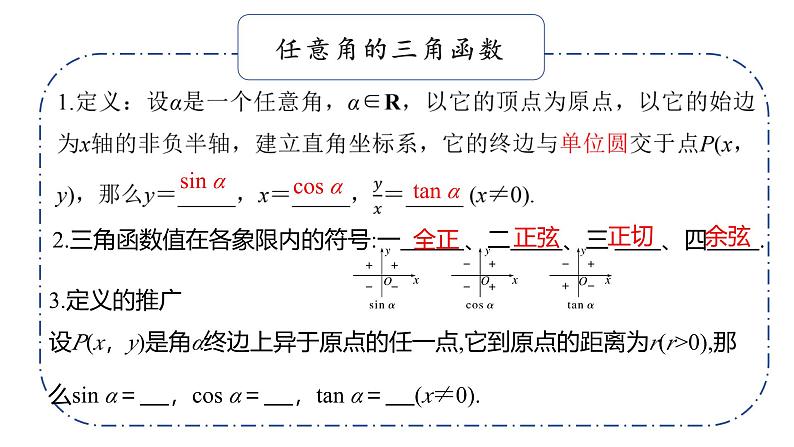
2.三角函数值在各象限内的符号:一 、二 、三 、四 .
3.定义的推广设P(x，y)是角α终边上异于原点的任一点,它到原点的距离为r(r>0),那么sin α＝ ，cs α＝ ，tan α＝ (x≠0).
1.同角三角函数的基本关系(1)平方关系： .(2)商数关系： .
2.同角三角函数的基本关系式的常见变形(1)sin2α＝1－cs2α ＝ ； cs2α＝ ＝(1＋sin α)(1－sin α)； (sin α±cs α)2＝ .
sin2α＋cs2α＝1
(1＋cs α)(1－cs α)
1±2sin αcs α
奇变偶不变，符号看象限
1.两角和与差的余弦、正弦、正切公式(1)公式C(α－β)：cs(α－β)＝ ；(2)公式C(α＋β)：cs(α＋β)＝ ；(3)公式S(α－β)：sin(α－β)＝ ；(4)公式S(α＋β)：sin(α＋β)＝ ；(5)公式T(α－β)：tan(α－β)＝ ；(6)公式T(α＋β)：tan(α＋β)＝ .
cs αcs β＋sin αsin β
cs αcs β－sin αsin β
sin αcs β－cs αsin β
sin αcs β＋cs αsin β
3.两角和与差的公式的常用变形：(1)sin αsin β＋cs(α＋β)＝ .(2)cs αsin β＋sin(α－β)＝ .(3)tan α±tan β＝ .
tan(α±β)(1∓tan αtan β)
1.二倍角的正弦、余弦、正切公式(1)sin 2α＝ .(2)cs 2α＝ ＝ ＝ .(3)tan 2α＝ .
2.二倍角公式的变形公式
*3.半角正切公式的有理化
cs2α－sin 2α
三角函数的图像与性质1
______________
三角函数的图像与性质2
[2kπ－π，2kπ]
[2kπ，2kπ＋π]
1.对称性与周期性(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是 个周期，相邻的对称中心与对称轴之间的距离是 个周期.(2)正切曲线相邻两对称中心之间的距离是 个周期.
2.与三角函数的奇偶性相关的结论(k∈Z)
(1)若y＝Asin(ωx＋φ)为偶函数,则φ＝ ;若为奇函数，则φ＝ .(2)若y＝Acs(ωx＋φ)为偶函数,则φ＝ ;若为奇函数，则φ＝ .(3)若y＝Atan(ωx＋φ)为奇函数,则φ＝ .
函数y＝Asin(ωx＋φ) (A>0，ω>0)
1.简谐运动的有关概念已知函数y＝Asin(ωx＋φ)(A>0，ω>0)，x≥0
2.用“五点法”画y＝Asin(ωx＋φ)一个周期内的简图时,要找五个特殊点
3.函数y＝sin x的图象经变换得到y＝Asin(ωx＋φ)的图象的两种途径
平移的规律：“ ， ”
平移的规律：“左加右减，上加下减”.
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
b2＋c2－2bccs A
c2＋a2－2cacs B
a2＋b2－2abcs C
sin A∶sin B∶sin C
(2)S＝ ＝ ＝ ；
(3)S＝ (r为三角形的内切圆半径).
2.在△ABC中，常有以下结论：(1)∠A＋∠B＋∠C＝ .(2)任意两边之和 第三边，任意两边之差 第三边.(3)a>b⇔A B⇔sin A sin B，cs A cs B.
4.在三角形中，若sinA=sinB,或csA=csB,则 必有 。（任意角中不一定成立）