数学第二册第7章 平面向量背景图ppt课件

这是一份数学第二册第7章 平面向量背景图ppt课件，共31页。PPT课件主要包含了第五章平面向量与复数，向量的有关概念，个单位长度，向量的线性运算1，b＋a，a＋b＋c，向量的线性运算2，λμa，λa＋μa，λa＋λb等内容，欢迎下载使用。
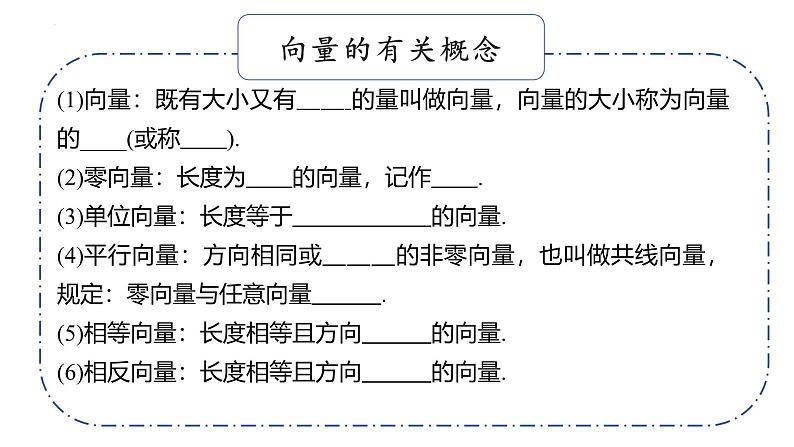
(1)向量：既有大小又有　　 的量叫做向量，向量的大小称为向量的____(或称　　).(2)零向量：长度为　　的向量，记作　　.(3)单位向量：长度等于　　　　　　的向量.(4)平行向量：方向相同或　　　的非零向量，也叫做共线向量，规定：零向量与任意向量　　　.(5)相等向量：长度相等且方向　　　的向量.(6)相反向量：长度相等且方向　　　的向量.
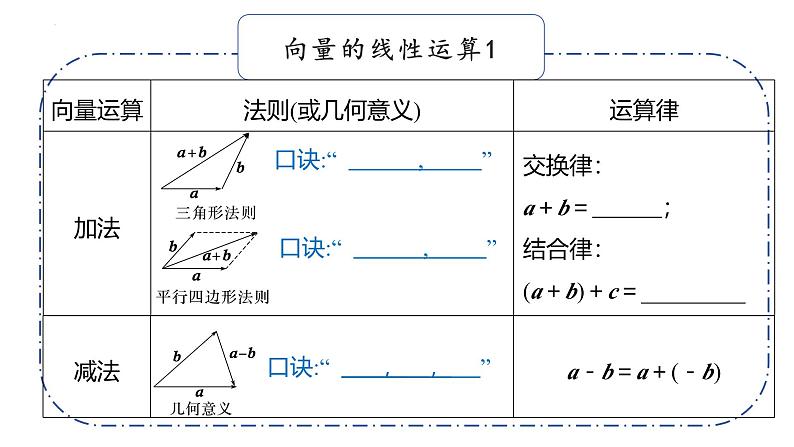
口诀:“ , ”
口诀:“ ， ， ”
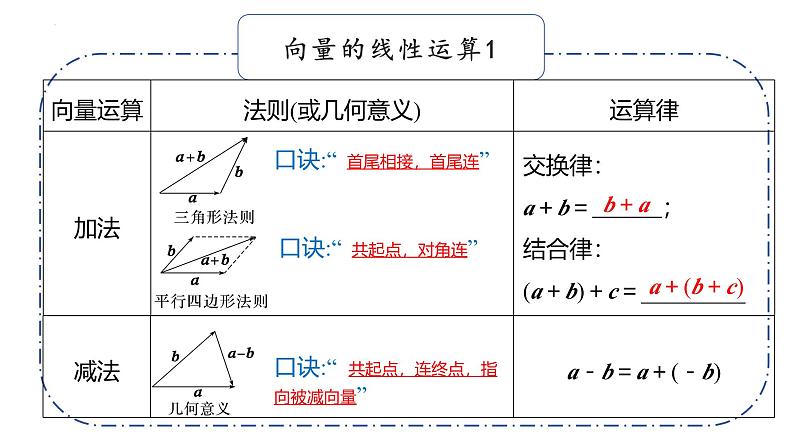
口诀:“ 首尾相接，首尾连”
口诀:“ 共起点，对角连”
口诀:“ 共起点，连终点，指向被减向量”
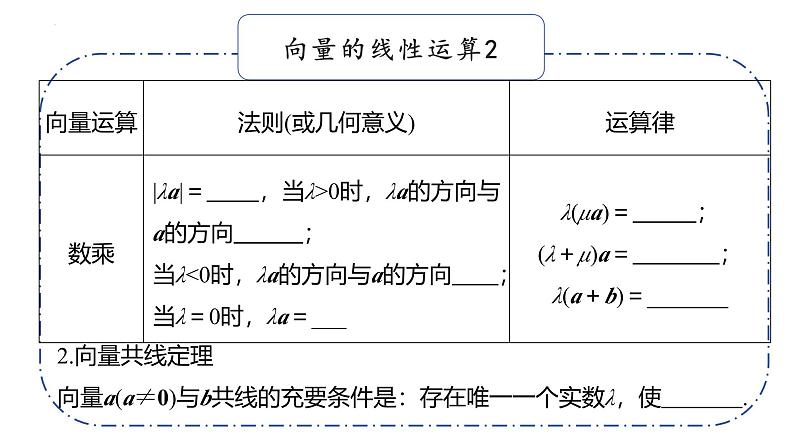
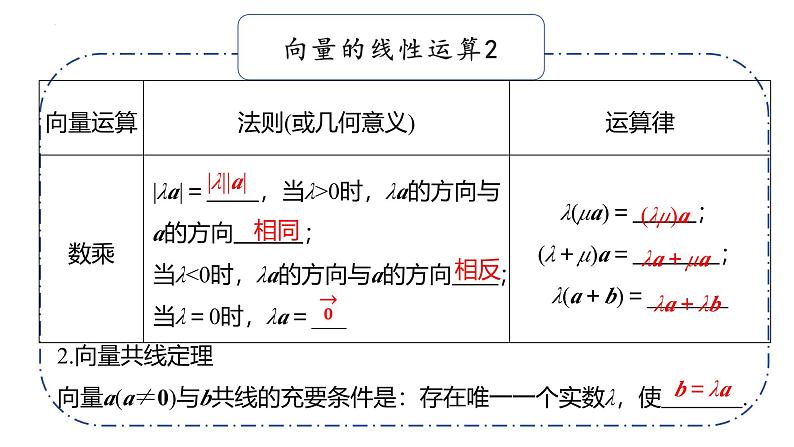
2.向量共线定理向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ，使 .
4.对于任意两个向量a，b，都有 ≤|a±b|≤ .
平面向量基本定理及坐标表示1
1.平面向量基本定理如果e1，e2是同一平面内的两个　　　　向量，那么对于这一平面内的任一向量a，　　　　　一对实数λ1，λ2，使a＝ .若e1，e2不共线,我们把{e1，e2}叫做表示这一平面内所有向量的一个　　 .2.平面向量的正交分解把一个向量分解为两个　　　　　的向量，叫做把向量作正交分解.
3.平面向量的坐标运算(1)设a＝(x1，y1)，b＝(x2，y2)，则a＋b＝　　　　　　　　，a－b＝　　　　　　　　，λa＝　　　　　，|a|＝　　　　　.
平面向量基本定理及坐标表示2
(2)向量坐标的求法①若向量的起点是坐标原点，则　　　坐标即为向量的坐标.
4.平面向量共线的坐标表示设a＝(x1，y1)，b＝(x2，y2)，其中b≠0，则a∥b⇔　　　　　　　.
5.已知△ABC,A(x1，y1)，B(x2，y2)，C(x3，y3)，P为线段AB的中点,则P( , )，△ABC重心为G，则G( , ).
(x1＋x2，y1＋y2)
(x1－x2，y1－y2)
(x2－x1，y2－y1)
x1y2－x2y1＝0
2.平面向量的数量积已知两个非零向量a与b，它们的夹角为θ，我们把数量 叫做向量a与b的数量积，记作 .
4.向量数量积的运算律(1)a·b＝ .(2)(λa)·b＝ ＝ .(3)(a＋b)·c＝ .
5.已知非零向量a＝(x1，y1)，b＝(x2，y2)，a与b的夹角为θ.
x1x2＋y1y2＝0
|a·b|≤|a||b|
|x1x2＋y1y2|≤
1.平面向量数量积运算的常用公式(1)(a＋b)·(a－b)＝ ； (2)(a±b)2＝ .2.有关向量夹角的两个结论(a与b为非零向量)(1)若a与b的夹角为锐角，则 ；若a·b>0，则a与b的夹角为 .(2)若a与b的夹角为钝角，则 ；若a·b0)表示 .
以(a，b)为圆心，r为半径的圆