






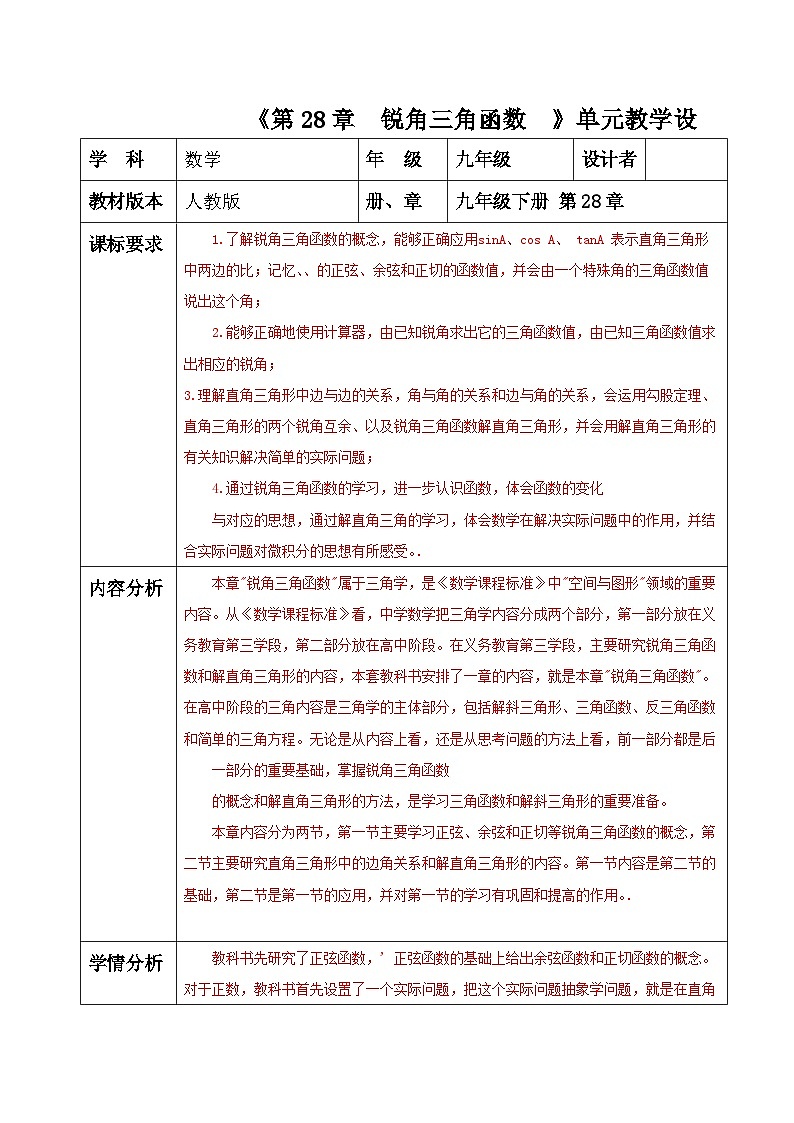
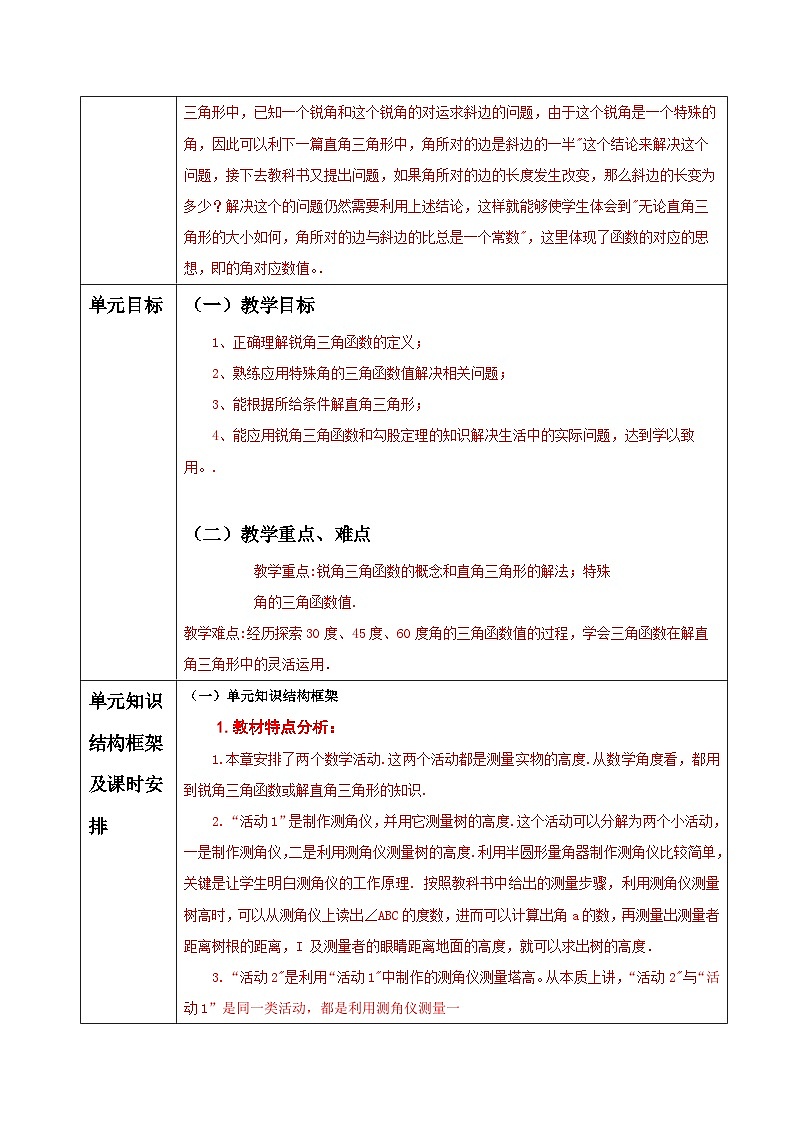

所属成套资源:【大单元核心素养】人教版数学九年级下册课件+教案+大单元整体教学设计
初中数学人教版(2024)九年级下册28.1 锐角三角函数试讲课教学ppt课件
展开
这是一份初中数学人教版(2024)九年级下册28.1 锐角三角函数试讲课教学ppt课件,文件包含281锐角三角函数1课件pptx、281锐角三角函数1教案docx、28章锐角三角函数单元整理分析教案docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
通过对30°和45°与其所对的直角边与斜边的比值之间关系的探讨,可以获得“直角三角形中,当锐角一定时,这个锐角的对边与斜边的比是固定值”这一重要结论,发展学生的演绎推理能力.在探索正弦函数概念的过程中,可进一步培养学生的创新意识,发展学生的形象思维,增强由特殊到一般逻辑推理能力.
1.理解锐角正弦的定义,掌握当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变). 2.能利用正弦概念解决相关问题.
比萨斜塔位于意大利中部比萨古城内的教堂广场上,该塔于1350年成时就已倾斜,其塔顶中心点偏离垂线中心线2.1米,1972年比萨地区发生地震,这座高AB=54.5米的斜塔大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2米.仔细看下图,你能用塔身中心线与垂直中心线所成的角度来描述比萨斜塔的倾斜程度吗?
从数学角度看,上述问题就是:已知直角三角形的某些边长,求其锐角的度数。对于直角三角形,我们已经知道三边之间、两个锐角之间的关系,它的边角之间有什么关系呢?下面我们一起来探究一下!
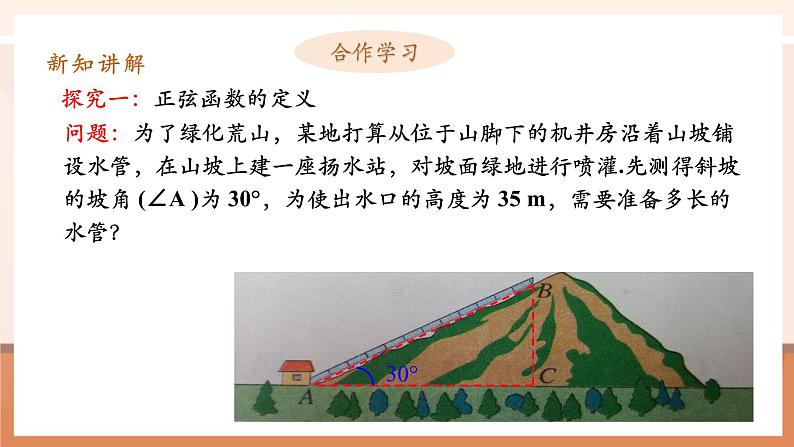
问题:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌.先测得斜坡的坡角 (∠A )为 30°,为使出水口的高度为 35 m,需要准备多长的水管?
探究一:正弦函数的定义
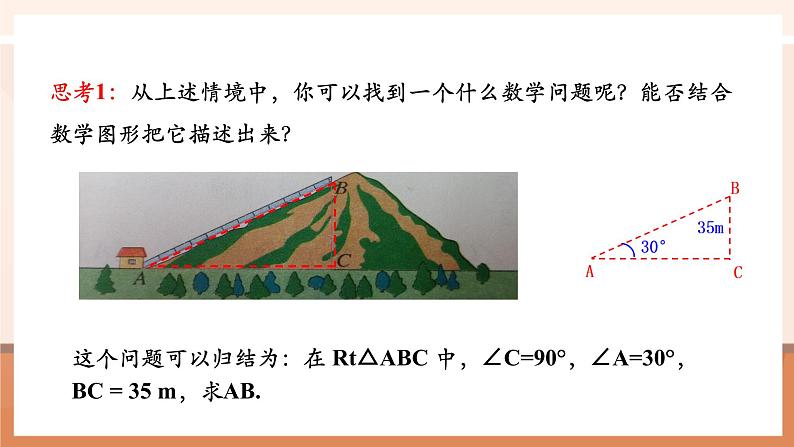
思考1:从上述情境中,你可以找到一个什么数学问题呢?能否结合数学图形把它描述出来?
这个问题可以归结为:在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
如图,在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
根据“在直角三角形中,30°角所对的边等于斜边的一半”, 即可得 AB = 2BC =2×35=70 (m). 也就是说,需要准备 70 m 长的水管.
思考2:如果出水口的高度为50 m,那么需要准备多长的水管?60米呢?
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
思考3:如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A的对边与斜边的比 由此你能得出什么结论?
解:因为∠A=45°,∠C=90°, 所以AC=BC,由勾股定理得: AB2=AC2+BC2=2BC2,
在直角三角形中,如果一个锐角等于45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
思考4:任意画 Rt△ABC 和 Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A’,那么 与 有什么关系?你能解释一下吗?
因为 所以Rt△ABC∽Rt△ 因此即 这就是说,在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个固定值.
注意:1.sinA不是sin与A的乘积,而是一个整体.2.正弦的三种表示方式:sinA,sin 56°,sin∠DEF.3.sinA是线段之间的一个比值,sinA没有单位.
sin∠DEF、 sin∠1 (不能省去角的符号)
sinA 、 sin39 °、 sinβ (省去角的符号)
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sin A,即 例如,当∠A=30°时,我们有 sin A=sin 30°= 当∠A=45°时,我们有 sin A=sin 45°=
∠A的正弦sin A随着∠A的变化而变化.
例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
解:如图(1),在Rt△ABC中,由勾股定理得
如图(2),在 Rt△ABC 中,由勾股定理得
计算一个锐角的正弦值要注意哪些问题?
要注意两个方面的问题:一是确定这个锐角所在的直角三角形;二是要注意正弦等于这个锐角的对边与斜边的比.
2. 在Rt△ABC中,∠C=90°,BC=2,sinA= 则边AC的长是( )A. B.3 C. D.
解析:如图, 而BC=2,
3. 如图,在 △ABC 中,∠ACB=90°,CD⊥AB. (1) sinB 可以由哪两条线段之比表示?
解:∵ CD⊥AB,∴∠ADC =∠ACB = 90°, ∴∠ACD = ∠B=90°-∠A,
(2) 若 AC = 5,CD = 3,求 sinB 的值.
解: 由 (1)知,
2. 如图,在 △ABC 中, AB = BC = 5,sinA = ,求△ABC 的面积.
解:作BD⊥AC于点D, ∵ sinA = ,
又∵ AB=AC ,BD⊥AC,∴ AC=2AD=6, ∴S△ABC=AC×BD÷2=12.
3.如图,在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4,求CD的长和sinC的值.
解:∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
∵AB=5,AD=4,∠ADB=90°,
∴CD=BC-BD=10.
∵AD=4,∠ADC=90°,
已知直角三角形的边长,求锐角的正弦值
已知锐角的正弦值,求直角三角形的边长
相关课件
这是一份初中人教版(2024)27.1 图形的相似优质教学课件ppt,文件包含271图形的相似1课件pptx、27章相似单元整理分析教案docx、271图形的相似1教案docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
这是一份人教版(2024)九年级下册29.2 三视图一等奖教学ppt课件,文件包含292三视图1课件pptx、292三视图1教案docx、29章投影与视图单元整理分析教案docx等3份课件配套教学资源,其中PPT共34页, 欢迎下载使用。
这是一份人教版(2024)九年级下册29.1 投影优秀教学课件ppt,文件包含291投影1课件pptx、291投影1教案docx、29章投影与视图单元整理分析教案docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。












