初中数学人教版（2024）七年级下册5.4 平移精品一课一练

这是一份初中数学人教版（2024）七年级下册5.4 平移精品一课一练，文件包含人教版数学七下培优提升训练专题54平移原卷版doc、人教版数学七下培优提升训练专题54平移解析版doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
注意事项：
本试卷满分120分，试题共24题，其中选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2022春•启东市期中）下列生活现象中，属于平移的是（ ）
A．升降电梯的上下移动B．荡秋千运动
C．把打开的课本合上D．钟摆的摆动
【分析】根据平移的性质，即可解答．
【解答】解：A、升降电梯的运动，属于平移现象，故A符合题意；
B、荡秋千运动，不属于平移现象，故B不符合题意；
C、把打开的课本合上，不属于平移现象，故B不符合题意；
D、钟摆的摆动，不属于平移现象，故D不符合题意；
故选：A．
2．（2022春•东莞市期中）下列选项中，由如图所示的“笑脸”平移得到的是（ ）
A．B．C．D．
【分析】根据平移的性质，结合图形，对选项进行一一分析，排除错误答案．
【解答】解：A．图案属于旋转所得到，故此选项不合题意；
B．图案属于旋转所得到，故此选项不合题意；
C．图案属于旋转所得到，故此选项不合题意；
D．图案形状与大小没有改变，符合平移性质，故此选项符合题意；
故选：D．
3．（2022春•增城区期中）如图，已知△ABC的周长为20cm，现将△ABC沿AB方向平移2cm至△A′B′C′的位置，连接CC′，则四边形AB′C′C的周长为（ ）
A．20cmB．22cmC．24cmD．26cm
【分析】根据平移的性质，经过平移，对应点所连的线段相等，对应线段相等，找出对应线段和对应点所连的线段，结合四边形的周长公式求解即可．
【解答】解：根据题意，得A的对应点为A′，B的对应点为B′，C的对应点为C′，
所以BC＝B′C′，BB′＝CC′，
则四边形AB′C′C的周长＝CA+AB+BB′+B′C′+C′C＝△ABC的周长+2BB′＝20+4＝24（cm）．
故选：C．
4．（2022春•白云区期中）如图，△ABC中，∠ABC＝90°，沿BC所在的直线向右平移得到△DEF，下列结论中，错误的（ ）
A．EC＝CFB．∠A＝∠DC．AC∥DFD．∠DEF＝90°
【分析】由平移的性质得出△ABC≌△DEF，得出对应边相等，对应角相等，即可得出结论．
【解答】解：∵Rt△ABC沿直角边BC所在的直线向右平移得到△DEF，
∴AC∥DF，△ABC≌△DEF，
∴∠ACB＝∠DFE，∠DEF＝∠ABC＝90°，AC＝DF，BC＝EF，∠A＝∠D，
∴AC∥DF，
∴BC﹣CE＝EF﹣CE，即BE＝CF，
∴选项B、C、D正确，不符合题意，
但BE不一定与EC相等，故选项A错误，符合题意；
故选：A．
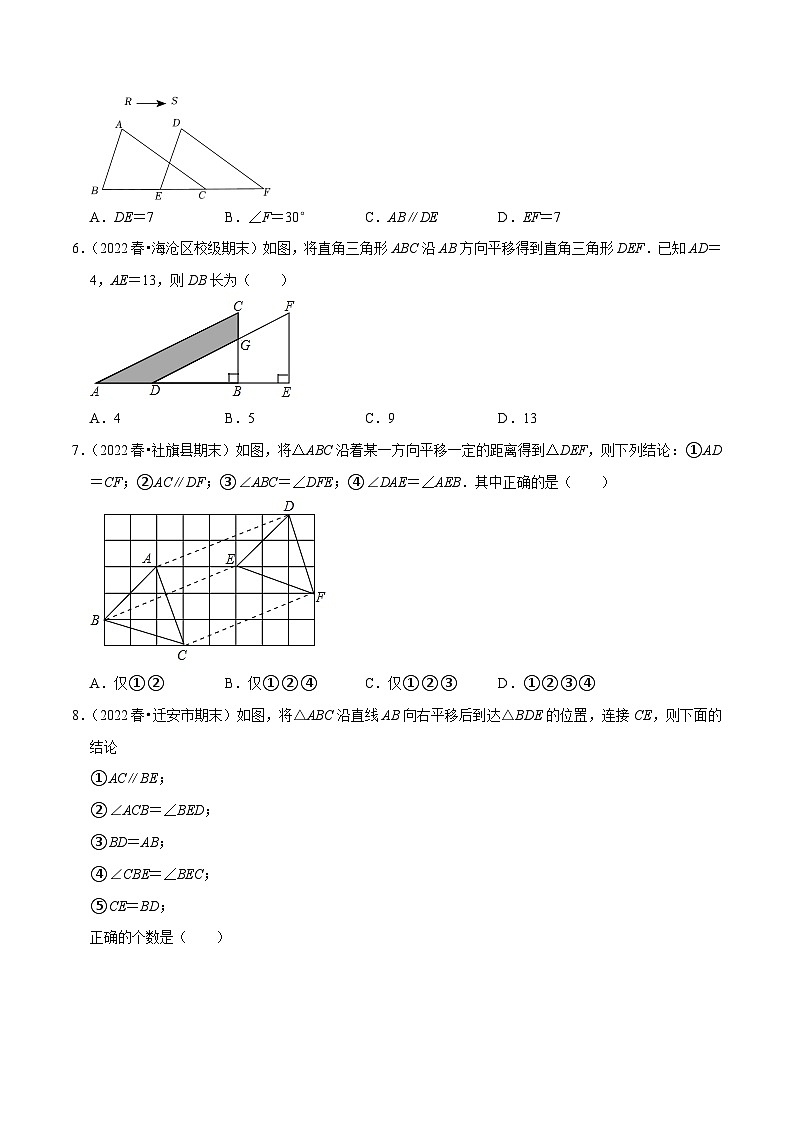
5．（2022春•海州区校级期末）如图，在△ABC中，BC＝7，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF的位置，若CF＝4，则下列结论中错误的是（ ）
A．DE＝7B．∠F＝30°C．AB∥DED．EF＝7
【分析】先根据三角形内角和定理计算出∠ACB＝30°，然后根据平移的性质对各选项进行判断．
【解答】解：∵∠A＝80°，∠B＝70°，
∴∠ACB＝30°，
∵△ABC沿RS的方向平移到△DEF的位置，
∴BE＝CF＝4，∠F＝∠ACB＝30°，所以B选项的结论正确；
DE＝AB，AB∥DE，EF＝BC＝7，所以A选项的结论错误，C选项的结论正确，D选项的结论错误．
故选：A．
6．（2022春•海沧区校级期末）如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知AD＝4，AE＝13，则DB长为（ ）
A．4B．5C．9D．13
【分析】证明AD＝BE，可得结论．
【解答】解：∵AB＝DE，
∴AD＝BE＝4，
∵AE＝13，
∴BD＝13﹣4﹣4＝5，
故选：B．
7．（2022春•社旗县期末）如图，将△ABC沿着某一方向平移一定的距离得到△DEF，则下列结论：①AD＝CF；②AC∥DF；③∠ABC＝∠DFE；④∠DAE＝∠AEB．其中正确的是（ ）
A．仅①②B．仅①②④C．仅①②③D．①②③④
【分析】根据平移的性质，对应点的连线互相平行且相等，平移变换只改变图形的位置不改变图形的形状与大小对各小题分析判断即可得解．
【解答】解：∵△ABC沿着某一方向平移一定的距离得到△DEF，
∴①AD∥CF，正确；
②AC＝DF，正确；
③∠ABC＝∠DEF，故原命题错误；
④∠DAE＝∠AEB，正确．
所以，正确的有①②④．
故选：B．
8．（2022春•迁安市期末）如图，将△ABC沿直线AB向右平移后到达△BDE的位置，连接CE，则下面的结论
①AC∥BE；
②∠ACB＝∠BED；
③BD＝AB；
④∠CBE＝∠BEC；
⑤CE＝BD；
正确的个数是（ ）
A．2B．3C．4D．5
【分析】根据平移的性质得到结论．
【解答】解：∵将△ABC沿直线AB向右平移后到达△BDE的位置，
∴AC∥BE，故①正确；△ACB≌△BED，AB＝CE＝BD，故③⑤正确；
∴∠ACB＝∠BED，度②正确；
∵将△ABC沿直线AB向右平移后到达△BDE的位置，
∴BC∥DE，
∴∠CBE＝∠BED，故④错误；
故选：C．
9．（2022秋•二道区校级月考）如图，将直角三角形ABC沿BC方向平移得到直角三角形DEF．若AB＝8cm，BE＝4cm，DH＝2cm，则图中阴影部分面积为（ ）
A．28cm2B．29cm2C．30cm2D．32cm2
【分析】根据平移性质利用梯形面积公式计算．
【解答】解：由平移可得△ABC≌△DEF，
∴S△ABC＝S△DEF，
∴S△ABC﹣S△HEC＝S△DEF﹣S△HEC，即S阴影＝S梯形ABEH，
又S梯形ABEH＝BE（HE+AB）＝×4×（8+8﹣2）＝28cm2．
故选：A．
10．（2022•南京模拟）如图，若四个完全相同的小直角三角形按如图方式全部放置在大直角三角形ABC的内部，这四个小三角形的斜边刚好相接在斜边BC上，AB+AC＝21，BC＝15，则这四个小直角三角形的直角边之和为（ ）
A．6B．15C．21D．36
【分析】利用平移的知识可得四个小直角三角形的直角边之和正好等于大直角三角形的两条直角边的和．
【解答】解：如图，将小直角三角形的直角边分别平移到大直角三角形的直角边上，
∴四个小直角三角形的直角边之和等于大直角三角形的两直角边之和21，
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2022春•如皋市期中）如图，将△ABC沿BC所在直线向右平移得到△DEF，若EC＝2，BF＝10，则平移的距离为 4 ．
【分析】利用平移的性质解决问题即可．
【解答】解：由平移的性质可知，BE＝CF，
∵BF＝10，EC＝2，
∴BE+CF＝10﹣2＝8，
∴BE＝CF＝4，
∴平移的距离为4，
故答案为：4．
12．（2022•南京模拟）如图，将△ABC沿着射线AC的方向平移到达△CDE的位置，若AE＝12cm，则线段BD的长是 6 cm．
【分析】根据平移的性质得到AC＝CE＝BD，然后利用AE＝AC+CE＝14cm求出CE即可．
【解答】解：∵△ABC沿着射线AC的方向平移到达△CDE的位置，
∴AC＝CE＝BD，
∵AE＝AC+CE＝12cm，
∴CE＝6cm，
∴BD＝6cm，
故答案为：6．
13．（2022春•榆次区期中）如图，将周长为18的△ABC沿BC方向平移3个单位长度得到△DEF，则四边形ABFD的周长为 24 ．
【分析】根据平移的性质可得AD＝CF＝3，AC＝DF，然后根据四边形的周长的定义列式计算即可得解．
【解答】解：∵△ABC沿BC方向平移3个单位得到△DEF，
∴AD＝CF＝3，AC＝DF，
∴四边形ABFD的周长＝AB+（BC+CF）+DF+AD＝AB+BC+AC+AD+CF，
∵△ABC的周长＝18，
∴AB+BC+AC＝18，
∴四边形ABFD的周长＝18+3+3＝24．
故答案为：24．
14．（2022春•息县期中）如图，将直角三角形ABC沿BC方向平移得到直角三角形DEF，其中AB＝6，BE＝3，DM＝2，则阴影部分的面积是 15 ．
【分析】根据平移的性质得到DE＝AB＝6，△DEF≌△ABC，根据梯形面积公式计算，得到答案．
【解答】解：由平移的性质可知：DE＝AB＝6，△DEF≌△ABC，
∴ME＝DE﹣DM＝6﹣2＝4，S△DEF＝S△ABC，
∴S阴影部分＝S△DEF﹣S△MEC
＝S△ABC﹣S△MEC
＝S梯形ABEM
＝×（4+6）×3
＝15，
故答案为：15．
15．（2022春•景谷县期末）如图，校园里长为10米，宽为8米的长方形草地内修建了宽为1米的道路，则草地面积是 56 平方米．
【分析】根据平移的性质可得，草地可看作是长为（10﹣2）米，宽为（8﹣1）米的矩形，然后进行计算即可解答．
【解答】解：由题意得：
（10﹣2）×（8﹣1）
＝8×7
＝56（平方米），
∴草地面积是56平方米，
故答案为：56．
16．（2022春•武江区校级期末）如图，某住宅小区有一长方形地块，若要在长方形地块内修筑同样宽的两条道路，道路宽为2m，余下部分绿化，则绿化的面积为 540m2 ．
【分析】根据平移的性质可得：绿化部分可看作是长为（32﹣2）米．宽为（20﹣2）米的矩形，然后进行计算即可解答．
【解答】解：由题意得：
（32﹣2）×（20﹣2）
＝30×18
＝540（m2），
∴绿化的面积为540m2，
故答案为：540m2．
17．（2022春•耒阳市期末）要在台阶上铺设某种红地毯，已知这种红地毯每平方米的售价是20元，台阶宽为3米，侧面如图所示，购买这种红地毯至少需要 600 元．
【分析】根据题意，结合图形，先把楼梯的横竖向上向右平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
【解答】解：利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为5.2米，4.8米，
∴地毯的长度为5.2+4.8＝10（米），
地毯的面积为10×3＝30（平方米），
∴购买这种红地毯至少需要30×20＝600（元）．
故答案为：600．
18．（2022春•庆云县期末）如图，两个直角三角形重叠在一起，将△ABC沿AB方向平移2cm得到△DEF，CH＝2cm，EF＝4cm，下列结论：①BH∥EF；②AD＝BE；③BD＝HF；④∠C＝∠BHD，以上结论正确的有 ①②④ （填序号）．
【分析】根据平移的性质、平行线的性质判断即可．
【解答】解：由平移的性质可知，BH∥EF，AB＝DE，AC∥DF，故①结论正确；
∵AB＝DE，
∴AB﹣BD＝DE﹣BD，即AD＝BE，故②结论正确；
∵BE＜HF，
∴AD＜HF，故③结论错误；
∵AC∥DF，
∴∠C＝∠BHD，故④结论正确；
故答案为：①②④．
三、解答题（本大题共6小题，共66分．解答时应写出文字说明、证明过程或演算步骤）
19．（2022春•盱眙县期中）如图，在边长为1个单位的正方形网格中，△ABC经过平移后得到△A'B'C'，图中标出了点B的对应点B'．根据下列条件，利用网格点和无刻度的直尺画图并解答相关的问题保留画图痕迹：
（1）画出△A'B'C'；
（2）连接AA'、CC'，那么AA'与CC'的关系是 AA'∥CC'，AA'＝CC' ，线段AC扫过的图形的面积为 10 ；
【分析】（1）根据平移的性质即可画出图形；
（2）根据平移的性质可得AA'∥CC'，AA'＝CC'，再根据四边形ACC'A'的面积为△ACA'面积的2倍可得线段AC扫过的图形面积．
【解答】解：（1）如图，△A'B'C'即为所求；
（2）根据平移的性质知，AA'∥CC'，AA'＝CC'，
线段AC扫过的图形为四边形CAA'C'，
∴四边形CAA'C'的面积为10，
故答案为：AA'∥CC'，AA'＝CC'，10．
20．（2022春•玄武区校级期中）如图，△ABC的顶点都在方格纸的格点上．
（1）在△ABC中画出BC边上的中线AM，AB边上的高CN；
（2）平移△ABC，使点B移动到点B'的位置，
①画出平移后的△A′B′C′；
②若连接AA′、BB′，则这两条线段之间的关系是 AA'＝BB'且AA'∥BB' ；
③平移过程中，AC边扫过的面积是 32 ．
【分析】（1）取BC的中点M，连接AM即可；根据三角形的高的定义，延长AB，过点C作AB的垂线即可．
（2）①根据平移的性质作图即可．
②由平移的性质可得出答案．
③连接CC'，由图可知，平移过程中，AC边扫过的面积即为四边形AA'C'C的面积，利用割补法求解即可．
【解答】解：（1）如图，AM，CN即为所求．
（2）①如图，△A′B′C′即为所求．
②由平移的性质可知，AA'＝BB'且AA'∥BB'．
故答案为：AA'＝BB'且AA'∥BB'．
③连接CC'，
平移过程中，AC边扫过的面积即为四边形AA'C'C的面积，
四边形AA'C'C的面积＝＝32．
故答案为：32．
21．（2022春•富阳区期中）在所给网格图（每个小格均为边长是1的正方形）中完成下列各题：
（1）作出△ABC向右平移4格，向下3格后所得的△A1B1C1；
（2）连接AA1，BB1，判断AA1，BB1的关系，并求△A1B1C1的面积．
【分析】（1）分别作出A，B，C的对应点A1，B1，C1即可．
（2）利用分割法求面积即可．
【解答】解：（1）如图△A1B1C1即为所求．
（2）AA1∥BB1，AA1＝BB1，四边形AA1B1B的面积＝7×5﹣2××3×4﹣2××2×3＝17．
22．（2022春•高淳区校级期中）如图，每个小正方形的边长均为1，每个小方格的顶点叫格点．
（1）画出△ABC中AB边上的高线CD，D为垂足；
（2）画出△ABC向右平移3个单位后得到的△A1B1C1；
（3）图中AB与A1B1的关系是 平行且相等 ；
（4）S△ABC的面积是 5 ．
【分析】（1）根据三角形高线的定义画出图形即可；
（2）利用平移变换的性质分别求出A，B，C的对应点即可解决问题；
（3）利用平移变换的性质判断即可；
（4）利用割补法求解即可．
【解答】解：（1）如图所示：
（2）如图所示：
（3）AB与A1B1的关系是平行且相等；
故答案为：平行且相等；
（4）S△ABC的面积＝，
故答案为：5．
23．（2022春•吴江区校级期中）如图，直线AB∥CD，MN⊥AB分别交AB，CD于点M、N，射线MP、MQ分别从MA、MN同时开始绕点M顺时针旋转，分别与直线CD交于点E、F，射线MP每秒转10°，射线MQ每秒转5°，ER，FR分别平分∠PED，∠QFC，设旋转时间为t秒（0＜t＜18）．
（1）①用含t的代数式表示：∠AMP＝ 10t °，∠QMB＝ （90﹣5t） °；
②当t＝4时，∠REF＝ 70 °．
（2）当∠MEN+∠MFN＝130°时，求出t的值；
（3）试探索∠EFR与∠ERF之间的数量关系，并说明理由；
（4）若∠PMN的角平分线与直线ER交于点K，∠EKM的度数是 45°或135° ．
【分析】（1）①根据题意可难得出∠AMP的度数为10t°，∠QMB＝90°﹣5t°；
②根据平行线的性质，可得∠MEF＝∠AME，再结合ER是∠PED的平分线，即可求解；
（2）由平行线的性质可得∠MEF＝∠AME＝10t°，再由MN⊥AB可得MN⊥CD，从而可得∠MFN＝90°﹣5t°，结合所给的条件∠MEN+∠MFN＝130°即可求解；
（3）∠EFR＝∠ERF，分别用含t的代数式表示出∠REF和∠EFR的度数，再结合三角形的内角和，可表示出∠ERF，进行比较即可求解；
（4）可分K在MN的左边与K在MN的右边两种情况进行讨论，再把△EKM的∠MEK和∠EMK的度数用含t的代数式表示出来，再利用三角形的内角和求∠EKM的度数即可．
【解答】解：（1）①由题意得：∠AMP＝10t°，∠NMF＝5t°，
∵AB∥CD，MN⊥AB，
∴∠QMB＝90°﹣∠NMF＝90°﹣5t°＝（90﹣5t）°；
故答案为：10t，（90﹣5t）；
②∵AB∥CD，
∴∠MEF＝∠AMP＝10t°，
∵ER是∠PED的平分线，
∴∠REF＝（180°﹣∠MEF）＝（180°﹣10t°）＝90°﹣5t°，
∴当t＝4时，∠REF＝90°﹣5×4°＝70°；
故答案为：70；
（2）①当点E在N左侧时，
∵AB∥CD，
∴∠MEN＝∠AMP＝10t°，
∵MN⊥AB，
∴MN⊥CD，
∵∠NMF＝5t°，
∴∠MFN＝90°﹣5t°，
∵∠MEN+∠MFN＝130°，
∴10t°+90°﹣5t°＝130°，
解得：t＝8；
②当点E在N右侧时，如图，
∵AB∥CD，∠AMP＝10t°，
∴∠MEN+∠AMP＝180°，
∴∠MEN＝180°﹣10t°，
∵MN⊥AB，
∴MN⊥CD，
∵∠NMF＝5t°，
∴∠MFN＝90°﹣5t°，
∵∠MEN+∠MFN＝130°，
∴180°﹣10t°+90°﹣5t°＝130°，
解得：t＝；
（3）∠EFR＝∠ERF，
理由：∵FR平分∠QFC，由（2）得∠MFN＝90°﹣5t°，
∴∠EFR＝（180°﹣∠MFN）＝（180°﹣90°+5t°）＝45°+t°，
∵由（1）得∠REF＝90°﹣5t°，
在△REF中，∠ERF＝180°﹣∠REF﹣∠EFR＝180°﹣（90°﹣5t°）﹣（45°+t°）＝45°+t°，
∴∠EFR＝∠ERF；
（4）①当K点在MN的左边时，如图所示：
由（2）得∠MEN＝10t°，
∴∠EMN＝90°﹣10t°，
∵MK是∠EMF的平分线，
∴∠EMK＝∠EMN＝45°﹣5t°，
由（1）得：∠REF＝90°﹣5t°，
∴∠MER＝∠REF+∠MEN＝90°﹣5t°+10t°＝90°+5t°，
在△MEK中，∠EKM＝180°﹣∠MER﹣∠EMK＝180°﹣（90°+5t°）﹣（45°﹣5t°）＝45°．
②当K点在MN的右边时，如图所示：
由题意可知：∠AMP＝10t°，则有∠MEN＝180°﹣∠AMP＝180°﹣10t°，
∠PMN＝10t°﹣90°，
∵MK平分∠PMN，ER平分∠PEF，∠PED＝∠MEN，
∴∠EMK＝∠PMN＝5t°﹣45°，∠MEK＝∠MEN＝∠PED＝90°﹣5t°，
在△MEK中，∠EKM＝180°﹣∠MEK﹣∠EMK＝180°﹣（90°﹣5t°）﹣（5t°﹣45°）＝135°．
故答案为：45°或135°．
24．（2022春•仓山区校级期中）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分∠AEF交CD于点M，且∠FEM＝∠FME．
（1）若2∠AEF＝∠MFE，求∠AEF的度数；
（2）如图2，点G是射线MD上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN＝α，∠EGF＝β．
①当点G在点F的右侧时，若β＝50°，求α的度数；
②当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．
【分析】（1）根据角平分线的定义结合题意推出AB∥CD，根据平行线的性质求解即可；
（2）①依据平行线的性质可得∠AEG＝130°，再根据EH平分∠FEG，EM平分∠AEF，即可得到∠HEN＝∠AEG＝65°，再根据HN⊥ME，即可得到Rt△EHN中，∠EHN＝90°﹣65°＝25°；
②分两种情况进行讨论：当点G在点F的右侧时，α＝β，当点G在FM上时，可得α＝90°﹣β．
【解答】解：（1）∵EM平分∠AEF，
∴∠AEM＝∠FEM，
∵∠FEM＝∠FME，
∴∠AEM＝∠FME，
∴AB∥CD，
∴∠AEF+∠MFE＝180°，
∵2∠AEF＝∠MFE，
∴3∠AEF＝180°，
∴∠AEF＝60°；
（2）①如图2中，
∵AB∥CD，
∴∠BEG＝∠EGF＝β＝50°，
∴∠AEG＝130°，
∵∠AEM＝∠MEF，∠HEF＝∠HEG，
∴∠HEN＝∠MEF+∠HEF＝∠AEG＝65°，
∵HN⊥EM，
∴∠HNE＝90°，
∴α＝∠EHN＝90°﹣∠HEN＝25°；
②结论：α＝β或α＝90°﹣β．
理由：当点G在F的右侧时，可得α＝β．
∵AB∥CD，
∴∠BEG＝∠EGF＝β，
∴∠AEG＝180°﹣β，
∵∠AEM＝∠MEF，∠HEF＝∠HEG，
∴∠HEN＝∠MEF+∠HEF＝∠AEG＝90°﹣β，
∵HN⊥EM，
∴∠HNE＝90°，
∴α＝∠EHN＝90°﹣∠HEN＝β．
当点G在FM上时，可得α＝90°﹣β．
理由：∵AB∥CD，
∴∠AEG＝∠EGF＝β，
又∵EH平分∠FEG，EM平分∠AEF，
∴∠HEF＝∠FEG，∠MEF＝∠AEF，
∴∠MEH＝∠MEF﹣∠HEF
＝（∠AEF﹣∠FEG）
＝∠AEG
＝β，
又∵HN⊥ME，
∴Rt△EHN中，∠EHN＝90°﹣∠MEH，
即α＝90°﹣β，