六年级上册数学培优奥数讲义-第26讲 数与形

这是一份六年级上册数学培优奥数讲义-第26讲 数与形，共8页。学案主要包含了三十年，还吃不到吗？”悟空说等内容，欢迎下载使用。
数与形是数学中的两个最古老、也是最基本的研究对象，它们在一定条件下可以相互转化。数与形是有联系的，这个联系称之为数形结合，或形数结合。数形结合的思想，其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，几何问题代数化。
数形结合的思想可以使某些抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷。
初级挑战1
根据上面图形与数的规律，接着这样排列下去，如果不画，你知道第10个数是多少吗？第n个数呢？
思路：第1个数是1，图形有1个；第2个数是4，图形有2×2＝4（个）；第3个数是9，图形有3×3＝9（个）……,这说明每个数与对应图形的个数相同，而第n个数可通过（ ）得到。
答案：10×10＝100，n×n＝n2
能力探索1
一些小圆形如下排列：
照这样画下去，第5个图形最外圈有（ ）个小圆形；第8个图形最外圈有（ ）个小圆形。
答案：第5个图形：62－42＝20，第8个图形：92－72＝32。
初级挑战2
如下图，摆1个正方形需4根火柴棒，摆2个正方形需7根火柴棒，摆3个正方形需10根火柴棒……
照这样摆下去，摆4个正方形需（ ）根火柴棒；摆10个正方形需（ ）根火柴棒；摆n个正方形需要（ ）根火柴棒。
摆一个正方形需要（ ）根火柴棒，后面每多摆一个正方形，就多需要（ ）根火柴棒，如果摆n个正方形，一共就要（ ）根火柴棒。
答案：摆4个正方形需13根火柴棒；摆10个正方形需31根火柴棒；摆n个正方形需要（3n＋1）根火柴棒。
能力探索2
1、按下列规律摆放☆，则第⑤堆☆有多少个？第⑨堆☆有多少个？
答案：第⑤堆☆有17个；第⑨堆☆有29个。
2、明明用小棒搭了3间房子(如下图所示)，像这样搭下去，搭5间房子要用_____根小棒；搭n间房子要用_________根小棒。
答案：搭5间房子要用26根小棒；搭n间房子要用（5n＋1）根小棒。
中级挑战1

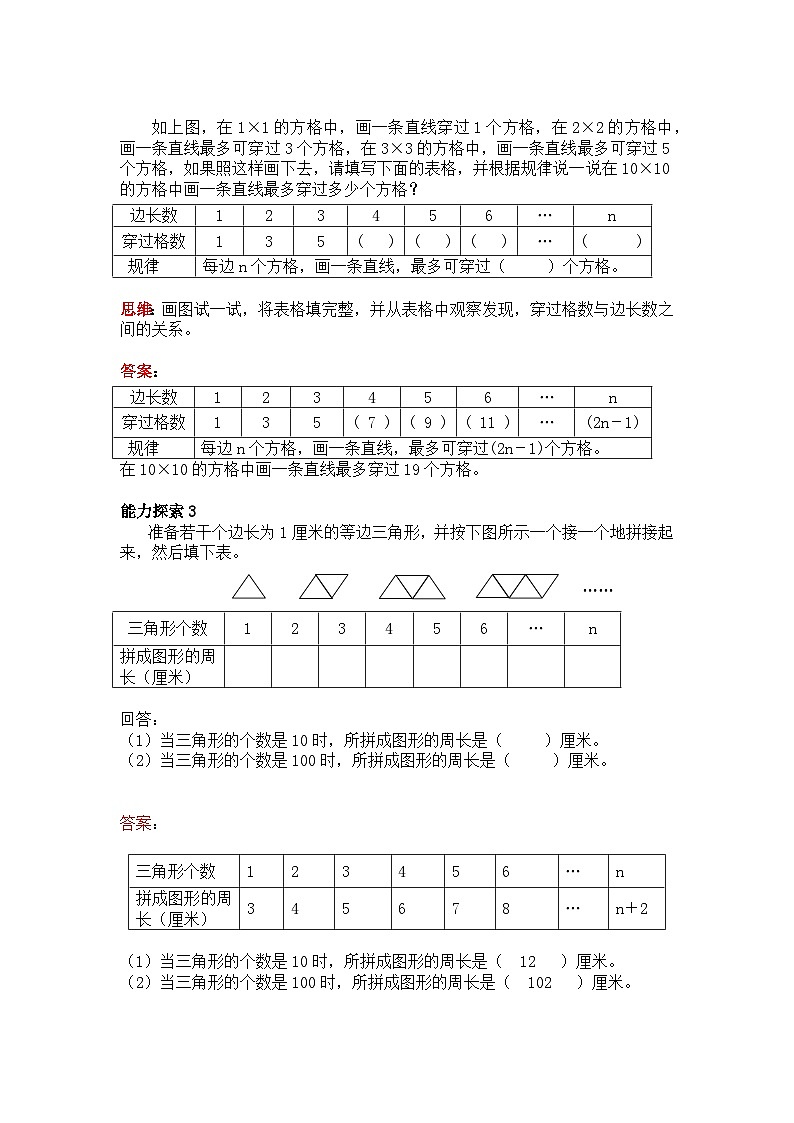
如上图，在1×1的方格中，画一条直线穿过1个方格，在2×2的方格中，画一条直线最多可穿过3个方格，在3×3的方格中，画一条直线最多可穿过5个方格，如果照这样画下去，请填写下面的表格，并根据规律说一说在10×10的方格中画一条直线最多穿过多少个方格？
思维：画图试一试，将表格填完整，并从表格中观察发现，穿过格数与边长数之间的关系。
答案：
在10×10的方格中画一条直线最多穿过19个方格。
能力探索3
准备若干个边长为1厘米的等边三角形，并按下图所示一个接一个地拼接起来，然后填下表。
回答：
（1）当三角形的个数是10时，所拼成图形的周长是（ ）厘米。
（2）当三角形的个数是100时，所拼成图形的周长是（ ）厘米。
答案：
（1）当三角形的个数是10时，所拼成图形的周长是（ 12 ）厘米。
（2）当三角形的个数是100时，所拼成图形的周长是（ 102 ）厘米。
中级挑战2
如下图①，在直角三角形ABC中，a、b、c分别是三角形三条边的长。用8个完全相同的直角三角形ABC，再做三个边长分别为a、b、c的正方形，把它们像图②和图③那样拼成两个大正方形。试根据图②和图③，说明：a2＋b2＝c2。

从图中可以看到，图②的面积是a2＋b2＋ab÷2×4＝a2＋b2＋2ab，图③的面积是ab÷2×4＋c2＝2ab＋c2，而这两个大正方形的边长都是a＋b，所以图②和图③面积相等。即a2＋b2＋2ab＝2ab＋c2，整理得a2＋b2＝c2。

能力探索4
如图，以直角三角形ABC的三条边为边，分别向外作正方形，那么三个正方形的面积有什么关系？试说明。
答案：S1＋S2＝S3。设△ABC的三边分别是a、b、c，因为△ABC是直角三角形，那么有a2＋b2＝c2，而S1＝ b2，S2＝ a2，S3＝c2，所以S1＋S2＝S3。
聪明泉
智斗猪八戒
话说唐僧师徒西天取经归来，来到郭家村，受到村民的热烈欢迎，大家都把他们当作除魔降妖的大英雄，不仅与他们合影留念，还拉他们到家里作客。
面对村民的盛情款待，师徒们觉得过意不去，一有机会就帮助他们收割庄稼，耕田耙地。开始几天猪八戒还挺卖力气，可过不了几天，好吃懒做的坏毛病又犯了。他觉得这样干活太辛苦了，师傅多舒服，只管坐着讲经念佛就什么都有了。其实师傅也没什么了不起的，要不是猴哥凭着他的火眼金睛和一身的本领，师傅恐怕连西天都去不了，更别说取经了。要是我也有这么一个徒弟，也能有一番作为，到那时，哈哈，我就可以享清福了。于是八戒就开始张落起这件事来，没几天就召收了9个徒弟，他给他们取名：小一戒、小二戒……小九戒。按理说，现在八戒应该潜心修炼，专心教导徒弟了。可是他仍然恶习不改，经常带着徒弟出去蹭吃蹭喝，吃得老百姓叫苦不迭。老百姓想着他们曾经为大家做的好事，谁也不好意思到悟空那里告状。就这样，八戒们更是有恃无恐，大开吃戒，一顿要吃掉五、六百个馒头，老百姓被他们吃得快揭不开锅了。
邻村有个叫灵芝的姑娘，她聪明伶俐，为人善良，经常用自己的智慧巧斗恶人。她听了这件事后，决定惩治一下八戒们。她来到郭家村，开了一个饭铺，八戒们闻讯赶来，灵芝姑娘假装惊喜地说：“悟能师傅，你能到我的饭铺，真是太荣幸了。以后你们就到我这儿来吃饭，不要到别的地方去了。”她停了一下说：“这儿有张圆桌，专门为你们准备的，你们十位每次都按不同的次序入座，等你们把所有的次序都坐完了，我就免费提供你们饭菜。但在此之前，你们每吃一顿饭，都必须为村里的一户村民做一件好事，你们看怎么样？”八戒们一听这诱人的建议，兴奋得不得了，连声说好。于是他们每次都按约定的条件来吃饭，并记下入座次序。这样过了几年，新的次序仍然层出不穷，八戒百思不得其解，只好去向悟空请教。悟空听了不禁哈哈大笑起来，说：“你这呆子，这么简单的帐都算不过来，还想去沾便宜，你们是永远也吃不到这顿免费饭菜的。”“难道我们吃二、三十年，还吃不到吗？”悟空说：“那我就给你算算这笔帐吧。我们先从简单的数算起。假设是三个人吃饭，我们先给他们编上1、2、3的序号，排列的次序就有6种，即123，132，213，231，312，321。如果是四个人吃饭，第一个人坐着不动，其他三个人的座位就要变换六次，当四个人都轮流作为第一个人坐着不动时，总的排列次序就是6×4＝24种。按就样的方法，可以推算出：五个人去吃饭，排列的次序就有24×5＝120种……10个人去吃饭就会有3628800种不同的排列次序。因为每天要吃3顿饭，用3628800÷3就可以算出要吃的天数：1209600天，也就是将近3320年。你们想想，你们能吃到这顿免费饭菜吗？”经悟空这么一算，八戒顿时明白了灵芝姑娘的用意，不禁羞愧万分。
从此以后，八戒经常带着徙弟们帮村民们干活，他们又重新赢得了人们的喜欢。
拓展挑战
你能利用下面的图发现a2－b2＝（a＋b）（a－b）这一公式吗？利用你所学的面积计算的知识，探索一下。
根据上图可知，a、b分别是两个正方形的边长，要求a2－b2，也就是求两个正方形的面积差，即左下图中阴影部分的面积。将图形如右下图所示转换，即可得出阴影部分面积是（a＋b）（a－b），所以a2－b2＝（a＋b）（a－b）。

能力探索5
如图，边长为（m＋3）厘米的正方形纸片，剪出一个边长为m厘米的正方形之后，剩下的部分可以剪拼成一个长方形（不重叠无缝隙），已知长方形的宽为3厘米，则它的长是（ ）厘米。
答案：2m＋3。剩下部分的面积是（m＋3）2－m2，利用上面公式有（m＋3）2－m2＝（m＋3＋m）（m＋3－m）＝（2m＋3）×3，所以长是2m＋3。
课堂小测
1、下面每个三角形图都是由一些相同的小三角形组成的。如果小三角形的边长是1，每个三角形的周长分别是多少？如果摆成一个n层的大三角形，它的周长又是多少？
答案：每个三角形的周长分别是3、6、9和12；如果摆成一个n层的大三角形，它的周长是3n。
2、我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》，他在这本著作中画了一个由数构成的三角形图，我们把它称为“杨辉三角”。
根据 “杨辉三角”每行的和与所在行的关系列表如下，请将表格填写完整。
答案：
3、观察如图的点子图，找一找有什么规律，想一想，第8个图里有_____个点，第n个图有__________个点。
答案：第8个图里有29个点，第n个图有4n－3个点。
※4、图中，S1～S7是各正方形的面积，你能说一说S7与其它几个正方形的面积关系吗？
答案：S7＝S3＋S6；而S3＝S1＋S2，S6＝S4＋S5，所以S7＝S1＋S2＋S4＋S5。边长数
1
2
3
4
5
6
…
n
穿过格数
1
3
5
( )
( )
( )
…
( )
规律
每边n个方格，画一条直线，最多可穿过（ ）个方格。
边长数
1
2
3
4
5
6
…
n
穿过格数
1
3
5
( 7 )
( 9 )
( 11 )
…
(2n－1)
规律
每边n个方格，画一条直线，最多可穿过(2n－1)个方格。
三角形个数
1
2
3
4
5
6
…
n
拼成图形的周长（厘米）
三角形个数
1
2
3
4
5
6
…
n
拼成图形的周长（厘米）
3
4
5
6
7
8
…
n＋2
行数
第1行
第2行
第3行
第4行
第5行
第6行
……
和
1
2
（ ）
（ ）
（ ）
（ ）
……
规律
后一行的和是前一行和的（ ）倍。
行数
第1行
第2行
第3行
第4行
第5行
第6行
……
和
1
2
（ 4 ）
（ 8 ）
（16）
（32）
……
规律
后一行的和是前一行和的（ 2 ）倍。