人教版数学九下同步讲义课件第二十八章 锐角三角函数（章末小结）

这是一份人教版数学九下同步讲义课件第二十八章 锐角三角函数（章末小结），共44页。
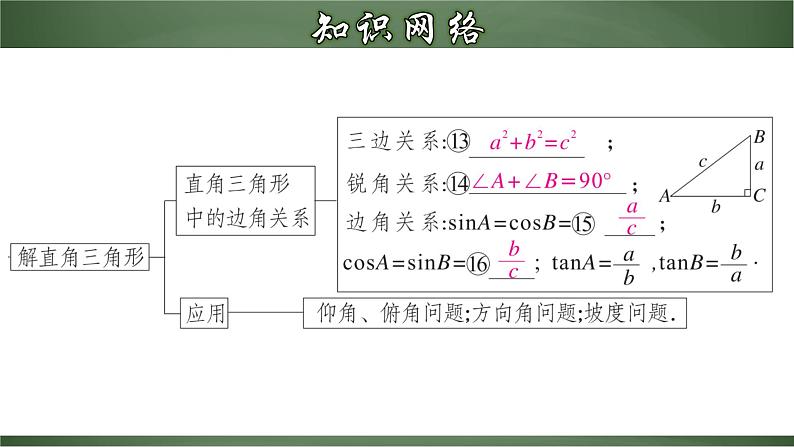
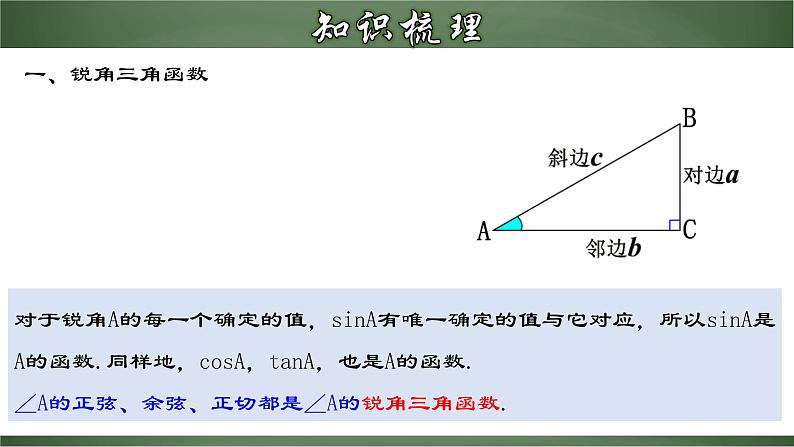
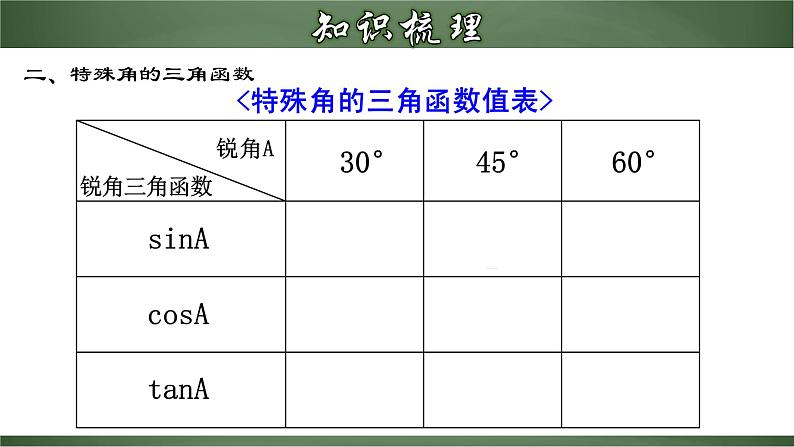
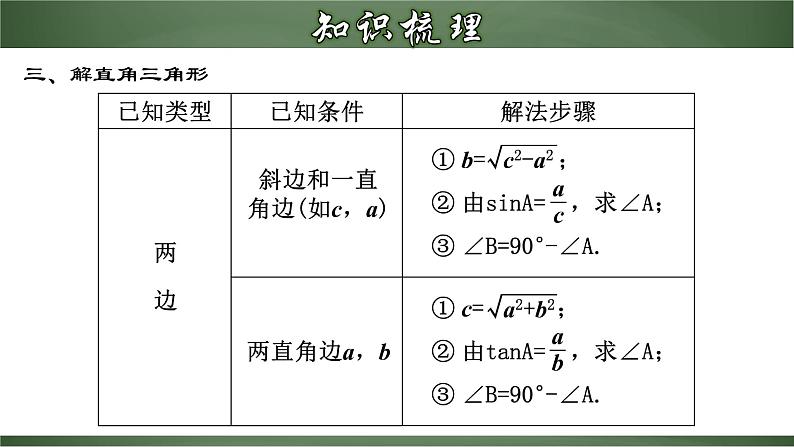
锐角三角函数章末小结1.准确掌握锐角三角函数定义能应用锐角三角函数定义进行有关边、角的计算.2.熟记特殊角的三角函数值能进行与特殊角的三角函数值有关的代数式的计算.3.会解直角三角形能通过添加辅助线构造直角三角形来解非直角三角形.4.运用解直角三角形的知识，灵活恰当地选择关系式解决实际问题.对于锐角A的每一个确定的值，sinA有唯一确定的值与它对应，所以sinA是A的函数.同样地，cosA，tanA，也是A的函数.∠A的正弦、余弦、正切都是∠A的锐角三角函数.一、锐角三角函数二、特殊角的三角函数三、解直角三角形 一般地，直角三角形中，除直角外，共有五个元素，即三条边和两个锐角. 由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形.(1)三边之间的关系 (2)两锐角之间的关系 (3)边角之间的关系∠A+∠B=90°a2+b2=c2(勾股定理) 三、解直角三角形三、解直角三角形四、解直角三角形的应用1.仰角和俯角在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.四、解直角三角形的应用以正南或正北方向为准，正南或正北方向线与目标方向线构成的小于90°的角，叫做方位角. 如图所示：2.方位角(1)坡度：如图，坡面的垂直高度h与水平宽度a的比叫做坡度(坡比)，即i= . (2)坡角：斜坡面与水平面的夹角α叫做坡角，l的长叫做坡面长.坡度与坡角的关系：tanα=i= .四、解直角三角形的应用3.坡度，坡角利用解直角三角形解决实际问题的一般过程：1.将实际问题抽象为数学问题；2.根据条件的特点，适当选用锐角三角函数去解直角三角形；画出平面图形，转化为解直角三角形的问题3.得到数学问题的答案；4.得到实际问题的答案.四、解直角三角形的应用例1.如图，在平面直角坐标系内有一点P(3，4)，连接OP，求OP与x轴正方向所夹锐角α的正弦值.解：过点P作PA⊥x轴，P(3，4)，∴A(3，0)A (0，3)在△APO中，由勾股定理得α【点睛】在直角三角形中，如果已知一边长及一个锐角的某个三角函数值，即可求出其它的所有锐角三角函数值  A   C【1-2】如图，在四边形ABCD中，∠DAB=90°,AD∥BC，AD=2BC,AC与BD交于点E,AC⊥BD，则tan∠BAC的值等于______.   例5.求下列各式的值：(1) (2)解：(1)原式 (2)原式    【2-1】求下列各式的值：(1)1-2sin30°cos30° (2)3tan30°-tan45°+2sin60°(3)(cos230°+sin230°)×tan60° a=60° β=45° B.a=30° β=45°C. a=30° β=60° D.a=60° β=60°DC D      C【3-2】如图，△ABC中，AB=12，BC=15，∠ABC=60°．求tanC的值．D   解:如图，过点E作EF⊥AC于F，则四边形CDEF为矩形.∴EF=CD，CF=DE=1Om由题意得∠DAC=∠ADC=45°，∠BEF=30°设AC=xm,则CD=EF=xm,BF=AC-CF-AB=(x-16)m在Rt△BEF中，tan∠BEF= 即 ，解得x≈37.8(m)答:乙楼AC的高度约为37.8m 例10.如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80nmile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处距离灯塔P有多远（精确到0.01nmile）？解：如图，在Rt△APC中，PC=PA•cos(90°-65°)=80×cos25°≈72.505 在Rt△BPC中，∠B=34°， ∵ sinB= ∴ PB= = ≈130(nmile) 因此，当海轮到达位于灯塔P的南偏东34°方向时，它距离灯塔P大约130nmile. (1)坡顶A到地面PQ的距离； H  HD 【4-1】如图，海中有一个小岛A，它的周围8nmile内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12nmile到达D点，这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行，有没有触礁的危险？