2023-2024学年上海市杨浦区七年级（上）期末数学试卷

这是一份2023-2024学年上海市杨浦区七年级（上）期末数学试卷，共16页。试卷主要包含了填空题，选择题，简答题，解答题等内容，欢迎下载使用。
1．（2分）用代数式表示：“a的平方的倒数减去b的差”是 ．
2．（2分）如果单项式﹣xm﹣2y2与4xyn是同类项，那么m﹣n＝ ．
3．（2分）用科学记数法表示：﹣0.0003025＝ ．
4．（2分）分解因式：x2+xy﹣2y2＝ ．
5．（2分）若分式的值为零，则x的值为 ．
6．（2分）如果3x2+px+q＝（3x+4）（x﹣2），那么p＝
7．（2分）计算：
8．（2分）计算： ．
9．（2分）一小包盐，加入245克热水化开后，变成一杯浓度为2%的盐水，这包盐有 克．
10．（2分）若关于x的方程有增根，那么k＝ ．
11．（2分）当2时，的值是 ．
12．（2分）如果存在一条直线把一个图形分割成两部分，使其中一部分沿某个方向平移后能与另一部分完全重合，那么我们把这个图形叫做平移重合图形．在①等腰梯形，②平行四边形，③圆这三个图形中， 是平移重合图形．（填序号）
13．（2分）如图，是由五个形状、大小都相同的正方形组成的图形，如果去掉其中一个正方形，使得剩下的图形是一个中心对称图形，那么不同的去法有 种．
14．（2分）如图，已知长方形纸片ABCD，AB＝10，AD＝x，AD＜AB．先将长方形纸片ABCD折叠，使点D落在AB边上，记作点D′，折痕为AE，再将△AED′沿D′E向右翻折，使点A落在射线D′B上，记作点A′．若翻折后的图形中，线段BD′＝3BA′，则x的值为 ．
二、选择题（本大题共4小题，每小题3分，共12分）
15．（3分）下列叙述中，正确的是（ ）
A．0是单项式
B．单项式23xy的次数是5
C．单项式的系数为﹣2
D．多项式3a3b+2a2是六次二项式
16．（3分）下列分式中，不是最简分式的是（ ）
A．B．
C．D．
17．（3分）下列说法中，正确的是（ ）
A．旋转对称图形一定是中心对称图形
B．角是轴对称图形，它的对称轴就是它的角平分线
C．轴对称图形可能有无数条对称轴
D．等边三角形既是中心对称图形，又是轴对称图形
18．（3分）在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是（ ）
A．点AB．点BC．点CD．点D
三、简答题（本大题共6小题，每小题6分，共36分）
19．（6分）计算：（﹣2a3）3÷a2+（a6﹣a3）•a．
20．（6分）计算：（结果不含负整数指数幂）．
21．（6分）因式分解：2a2﹣6bc+4ab﹣3ac．
22．（6分）因式分解：﹣2mnx2+m2x2+n2x2﹣4（m﹣n）2．
23．（6分）解方程：．
24．（6分）化简并求值：（x+1），其中x＝2﹣1．
四、解答题（本大题共4小题，每小题6分，共24分）
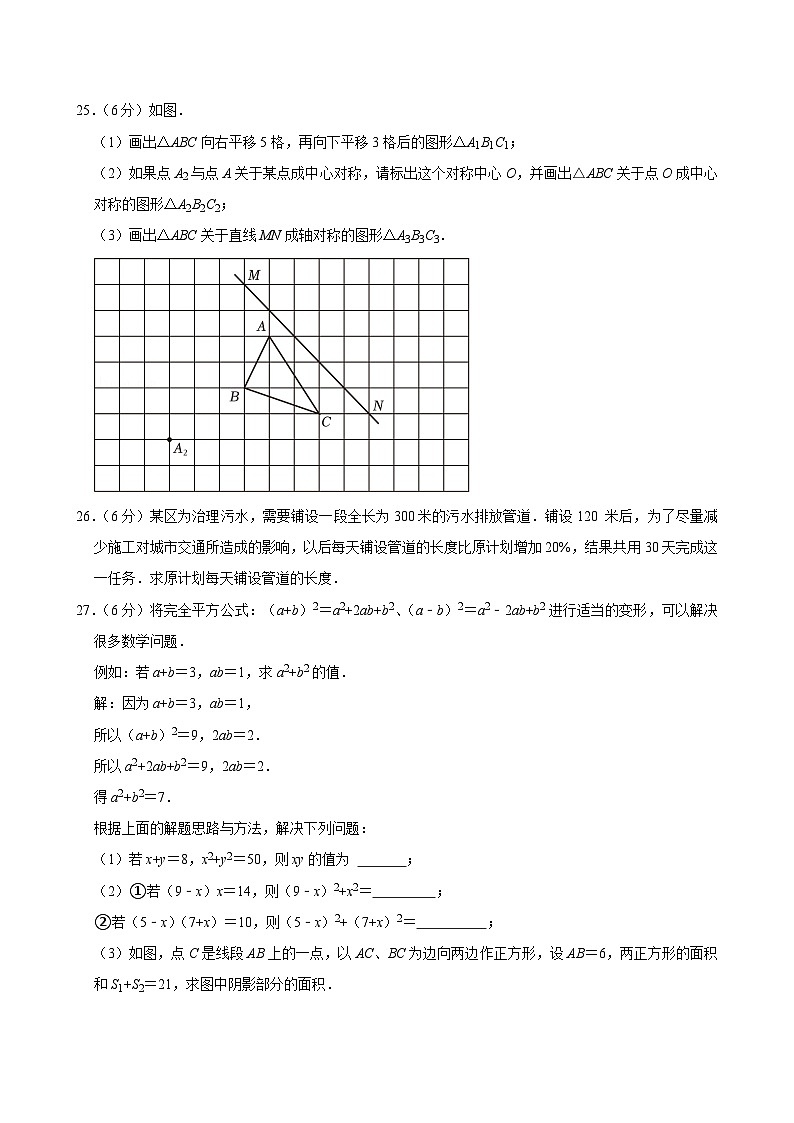
25．（6分）如图．
（1）画出△ABC向右平移5格，再向下平移3格后的图形△A1B1C1；
（2）如果点A2与点A关于某点成中心对称，请标出这个对称中心O，并画出△ABC关于点O成中心对称的图形△A2B2C2；
（3）画出△ABC关于直线MN成轴对称的图形△A3B3C3．
26．（6分）某区为治理污水，需要铺设一段全长为300米的污水排放管道．铺设120 米后，为了尽量减少施工对城市交通所造成的影响，以后每天铺设管道的长度比原计划增加20%，结果共用30天完成这一任务．求原计划每天铺设管道的长度．
27．（6分）将完全平方公式：（a+b）2＝a2+2ab+b2、（a﹣b）2＝a2﹣2ab+b2进行适当的变形，可以解决很多数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：因为a+b＝3，ab＝1，
所以（a+b）2＝9，2ab＝2．
所以a2+2ab+b2＝9，2ab＝2．
得a2+b2＝7．
根据上面的解题思路与方法，解决下列问题：
（1）若x+y＝8，x2+y2＝50，则xy的值为 ；
（2）①若（9﹣x）x＝14，则（9﹣x）2+x2＝ ；
②若（5﹣x）（7+x）＝10，则（5﹣x）2+（7+x）2＝ ；
（3）如图，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝6，两正方形的面积和S1+S2＝21，求图中阴影部分的面积．
28．（6分）如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°，将一把含45°角的直角三角尺的直角顶点放在点O处，一直角边OM与直线AB重合，另一直角边ON、斜边MN都在直线AB的下方．
（1）将图1中的三角尺绕点O按逆时针方向旋转60°，如图2所示，此时∠CON＝ ；
（2）将图1中的三角尺绕点O按逆时针方向旋转一个角度α（0°＜α＜360°），
①当旋转的角度α为何值时，射线OC所在的直线是△OMN的对称轴；
②是否存在相应的旋转角度α使得∠COM与∠CON互补？若存在，请直接写出α的值；若不存在，请说明理由．
2023-2024学年上海市杨浦区七年级（上）期末数学试卷
参考答案与试题解析
一、填空题（本大题共14小题，每小题2分，共28分）
1．（2分）用代数式表示：“a的平方的倒数减去b的差”是 b ．
【解答】解：“a的平方的倒数减去b的差”用代数式表示为：b，
故答案为：b．
2．（2分）如果单项式﹣xm﹣2y2与4xyn是同类项，那么m﹣n＝ 1 ．
【解答】解：∵单项式﹣xm﹣2y2与4xyn是同类项，
∴m﹣2＝1，n＝2，
∴m＝3，
∴m﹣n＝3﹣2＝1．
故答案为：1．
3．（2分）用科学记数法表示：﹣0.0003025＝ ﹣3.025×10﹣4 ．
【解答】解：﹣0.0003025＝﹣3.025×10﹣4；
故答案为：﹣3.025×10﹣4．
4．（2分）分解因式：x2+xy﹣2y2＝ （x+2y）（x﹣y） ．
【解答】解：x2+xy﹣2y2＝（x+2y）（x﹣y）．
故答案为：（x+2y）（x﹣y）．
5．（2分）若分式的值为零，则x的值为 ﹣1 ．
【解答】解：由题意，得
x2﹣1＝0且1﹣x≠0，
解得x＝﹣1．
故答案为：﹣1．
6．（2分）如果3x2+px+q＝（3x+4）（x﹣2），那么p＝ ﹣2
【解答】解：∵（3x+4）（x﹣2）＝3x2﹣2x﹣8，3x2+px+q＝（3x+4）（x﹣2），
∴p＝﹣2．
故答案为：﹣2．
7．（2分）计算： ﹣8
【解答】解：原式＝﹣22023×（）2020
＝﹣22020×（）2020×23
＝﹣1×8
＝﹣8．
故答案为：﹣8．
8．（2分）计算： 4m3+3m﹣2 ．
【解答】解：

＝4m3+3m﹣2，
故答案为：4m3+3m﹣2．
9．（2分）一小包盐，加入245克热水化开后，变成一杯浓度为2%的盐水，这包盐有 5 克．
【解答】解：设这包盐有x克，
100%＝2%，
解得x＝5，
故答案为：5．
10．（2分）若关于x的方程有增根，那么k＝ 6 ．
【解答】解：方程两边同时乘以x﹣3得：
2x﹣k＝x﹣3，
x＝k﹣3，
∵分式方程的增根是x＝3，
∴k﹣3＝3，
即k＝6．
故答案为：6．
11．（2分）当2时，的值是 ．
【解答】解：当2时，
，
故的值是．
故答案为．
12．（2分）如果存在一条直线把一个图形分割成两部分，使其中一部分沿某个方向平移后能与另一部分完全重合，那么我们把这个图形叫做平移重合图形．在①等腰梯形，②平行四边形，③圆这三个图形中， ② 是平移重合图形．（填序号）
【解答】解：如图，平行四边形ABCD中，取BC，AD的中点E，F，连接EF．
∵四边形ABEF向右平移可以与四边形EFDC重合，
∴平行四边形ABCD是平移重合图形，
故答案为：②．
13．（2分）如图，是由五个形状、大小都相同的正方形组成的图形，如果去掉其中一个正方形，使得剩下的图形是一个中心对称图形，那么不同的去法有 2 种．
【解答】解：去掉一个正方形，得到中心对称图形，如图所示：
，
共2种方法．
故答案为：2．
14．（2分）如图，已知长方形纸片ABCD，AB＝10，AD＝x，AD＜AB．先将长方形纸片ABCD折叠，使点D落在AB边上，记作点D′，折痕为AE，再将△AED′沿D′E向右翻折，使点A落在射线D′B上，记作点A′．若翻折后的图形中，线段BD′＝3BA′，则x的值为 或 ．
【解答】解：①当点A′在D′B上时，BD′＝3BA′，
∴AD′＝D′B＝BA′＝x cm，
∴2.5x＝10，
∴x＝4．
②如图所示，当点A′在AB的延长线上时，
由题意知，AD＝AD′＝A′D′＝x，
∵AB＝10，
∴BD′＝10﹣x，A′B＝2x﹣10，
由BD′＝3BA′得10﹣x＝3（2x﹣10），
解得：x．
综上所述，满足条件的x的值为或．
故答案为：4或．
二、选择题（本大题共4小题，每小题3分，共12分）
15．（3分）下列叙述中，正确的是（ ）
A．0是单项式
B．单项式23xy的次数是5
C．单项式的系数为﹣2
D．多项式3a3b+2a2是六次二项式
【解答】解：0是单项式，则A符合题意；
单项式23xy的次数是2，则B不符合题意；
单项式的系数为，则C不符合题意；
多项式3a3b+2a2是四次二项式，则D不符合题意；
故选：A．
16．（3分）下列分式中，不是最简分式的是（ ）
A．B．
C．D．
【解答】解：A、是最简分式，不符合题意；
B、不是最简分式，符合题意；
C、是最简分式，不符合题意；
D、是最简分式，不符合题意；
故选：B．
17．（3分）下列说法中，正确的是（ ）
A．旋转对称图形一定是中心对称图形
B．角是轴对称图形，它的对称轴就是它的角平分线
C．轴对称图形可能有无数条对称轴
D．等边三角形既是中心对称图形，又是轴对称图形
【解答】解：A．旋转对称图形不一定是中心对称图形，原说法错误，故本选项不符合题意；
B．角是轴对称图形，角的对称轴就是它的角平分线所在直线，原说法错误，故本选项不符合题意；
C．轴对称图形可能有无数条对称轴，如圆是轴对称图形，有无数条对称轴，原说法左起，故本选项符合题意；
D．等边三角形是轴对称图形，但不是中心对称图形，原说法错误，故本选项不符合题意．
故选：C．
18．（3分）在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是（ ）
A．点AB．点BC．点CD．点D
【解答】解：∵△MNP绕某点旋转一定的角度，得到△M1N1P1，
∴连接PP1、NN1、MM1，
作PP1的垂直平分线过B、D、C，
作NN1的垂直平分线过B、A，
作MM1的垂直平分线过B，
∴三条线段的垂直平分线正好都过B，
即旋转中心是B．
故选：B．
三、简答题（本大题共6小题，每小题6分，共36分）
19．（6分）计算：（﹣2a3）3÷a2+（a6﹣a3）•a．
【解答】解：（﹣2a3）3÷a2+（a6﹣a3）•a
＝﹣8a3×3﹣2+a6+1﹣a3+1
＝﹣8a7+a7﹣a4
＝﹣7a7﹣a4．
20．（6分）计算：（结果不含负整数指数幂）．
【解答】解：






＝y．
21．（6分）因式分解：2a2﹣6bc+4ab﹣3ac．
【解答】解：2a2﹣6bc+4ab﹣3ac
＝（2a2+4ab）﹣（6bc+3ac）
＝2a（a+2b）﹣3c（2b+a）
＝（a+2b）（2a﹣3c）．
22．（6分）因式分解：﹣2mnx2+m2x2+n2x2﹣4（m﹣n）2．
【解答】解：﹣2mnx2+m2x2+n2x2﹣4（m﹣n）2
＝（﹣2mnx2+m2x2+n2x2）﹣4（m﹣n）2
＝x2（﹣2mn+m2+n2）﹣4（m﹣n）2
＝x2（m﹣n）2﹣4（m﹣n）2
＝（m﹣n）2（x2﹣4）
＝（m﹣n）2（x﹣2）（x+2）．
23．（6分）解方程：．
【解答】解：方程的两边同乘x（x﹣1），
得：x+5＝5x﹣3（x﹣1），
解得：x＝2．
检验：把x＝2代入x（x﹣1）＝2≠0，即x＝2是原分式方程的解．
则原方程的解为：x＝2．
24．（6分）化简并求值：（x+1），其中x＝2﹣1．
【解答】解：原式•
•
•
，
当x＝2﹣1时，原式．
四、解答题（本大题共4小题，每小题6分，共24分）
25．（6分）如图．
（1）画出△ABC向右平移5格，再向下平移3格后的图形△A1B1C1；
（2）如果点A2与点A关于某点成中心对称，请标出这个对称中心O，并画出△ABC关于点O成中心对称的图形△A2B2C2；
（3）画出△ABC关于直线MN成轴对称的图形△A3B3C3．
【解答】解：（1）如图，△A1B1C1即为所求．
（2）如图，点O和△A2B2C2即为所求．
（3）如图，△A3B3C3即为所求．
26．（6分）某区为治理污水，需要铺设一段全长为300米的污水排放管道．铺设120 米后，为了尽量减少施工对城市交通所造成的影响，以后每天铺设管道的长度比原计划增加20%，结果共用30天完成这一任务．求原计划每天铺设管道的长度．
【解答】解：原计划每天铺设管道x米；
列方程：，
解得 x＝9，
经检验 x＝9是原方程的解且符合题意；
答：原计划每天铺设管道9 米．
27．（6分）将完全平方公式：（a+b）2＝a2+2ab+b2、（a﹣b）2＝a2﹣2ab+b2进行适当的变形，可以解决很多数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：因为a+b＝3，ab＝1，
所以（a+b）2＝9，2ab＝2．
所以a2+2ab+b2＝9，2ab＝2．
得a2+b2＝7．
根据上面的解题思路与方法，解决下列问题：
（1）若x+y＝8，x2+y2＝50，则xy的值为 7 ；
（2）①若（9﹣x）x＝14，则（9﹣x）2+x2＝ 53 ；
②若（5﹣x）（7+x）＝10，则（5﹣x）2+（7+x）2＝ 124 ；
（3）如图，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝6，两正方形的面积和S1+S2＝21，求图中阴影部分的面积．
【解答】解：（1）∵x+y＝8，x2+y2＝50，
∴（x+y）2＝64，
x2+y2+2xy＝64，
2xy＝64﹣50，
2xy＝14，
xy＝7，
故答案为：7；
（2）①∵（9﹣x）x＝14，
∴2x（9﹣x）＝28，
∵[（9﹣x）+x]2
＝（9﹣x+x）2
＝92
＝81，
∴（9﹣x）2+x2+2x（9﹣x）＝81，
（9﹣x）2+x2＝81﹣2x（9﹣x），
（9﹣x）2+x2＝81﹣28＝53，
故答案为：53；
②∵（5﹣x）（7﹣x）＝10，
∴2（5﹣x）（7﹣x）＝20，
∵[（5﹣x）+（7+x）]2
＝（5﹣x+7+x）2
＝122
＝144，
∴（5﹣x）2+（7+x）2+2（5﹣x）（7+x）＝144，
（5﹣x）2+（7+x）2＝144﹣20，
（5﹣x）2+（7+x）2＝124，
（3）设AC＝x，BC＝y，
∵，
∴x2+y2＝21，
∵AB＝AC+BC＝6，
∴x+y＝6，
∴（x+y）2＝36，
x2+y2+2xy＝36，
21+2xy＝36，
2xy＝36﹣21，
2xy＝15，
，
∴阴影部分的面积为：．
28．（6分）如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°，将一把含45°角的直角三角尺的直角顶点放在点O处，一直角边OM与直线AB重合，另一直角边ON、斜边MN都在直线AB的下方．
（1）将图1中的三角尺绕点O按逆时针方向旋转60°，如图2所示，此时∠CON＝ 150° ；
（2）将图1中的三角尺绕点O按逆时针方向旋转一个角度α（0°＜α＜360°），
①当旋转的角度α为何值时，射线OC所在的直线是△OMN的对称轴；
②是否存在相应的旋转角度α使得∠COM与∠CON互补？若存在，请直接写出α的值；若不存在，请说明理由．
【解答】解：（1）∵∠BOC＝120°，
∴直角三角尺绕点O按逆时针方向旋转60°后，∠BON＝30°，
∴∠CON＝∠BOC+∠BON＝150°，
故答案为：150°；
（2）①当直角三角尺绕点O按逆时针方向旋转到如下（一）位置时
∵∠MON＝90°，△OMN关于直线OC对称轴，
∴∠MOC＝45°，
∴此时α＝120°+45°＝165°，
②当直角三角尺绕点O按逆时针方向旋转到如下（二）位置时
∵∠BOC＝120°，
∴∠BOM＝180°﹣120°﹣45°＝15°，
∴此时α＝360°﹣15°＝345°，
答：当旋转165°或者345°时，射线OC所在的直线是△OMN的对称轴；
（3）存在旋转角度α使得∠COM与∠CON互补，
证明：∵∠COM＝120°，∠CON＝210°，
∴120°﹣α+210°﹣α＝180°，
∴α＝75°．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/12/6 16:00:47；用户：刘亚君；邮箱：99197645@qq.cm；学号：2798877题号
15
16
17
18
答案
A
B
C
B