江苏无锡市东林中学2024-2025学年八上数学第14周阶段性训练模拟练习【含答案】

这是一份江苏无锡市东林中学2024-2025学年八上数学第14周阶段性训练模拟练习【含答案】，共20页。试卷主要包含了已知点P在直线l等内容，欢迎下载使用。
1．在△ABC中，AB＝AC，∠BAC＝45°，边AC、BC上的高BE、AD交点F．若BD=2，则AF的长为（ ）
A．1B．2C．3D．22
2．如图，∠ABC＝∠ADC＝90°，∠BAD＝70°，点E是AC的中点．则∠EBD的度数为（ ）
A．20°B．35°C．40°D．55°
3．A、B两地相距20千米，甲、乙两人都从A地去B地，图中l1和l2分别表示甲、乙两人所走路程s（千米）与时间t（小时）之间的关系．下列说法错误的是（ ）
A．乙晚出发1小时B．乙出发3小时后追上甲
C．甲的速度是4千米/小时D．乙先到达B地
4．如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）
A．54B．1C．2D．52
5．如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（ ）
A．2B．2+1C．1−2D．−2
二．填空题（共5小题）
6．如图，直线y＝kx+b与直线y＝﹣x相交于点A，则关于x的不等式﹣x＜kx+b的解集为 ．
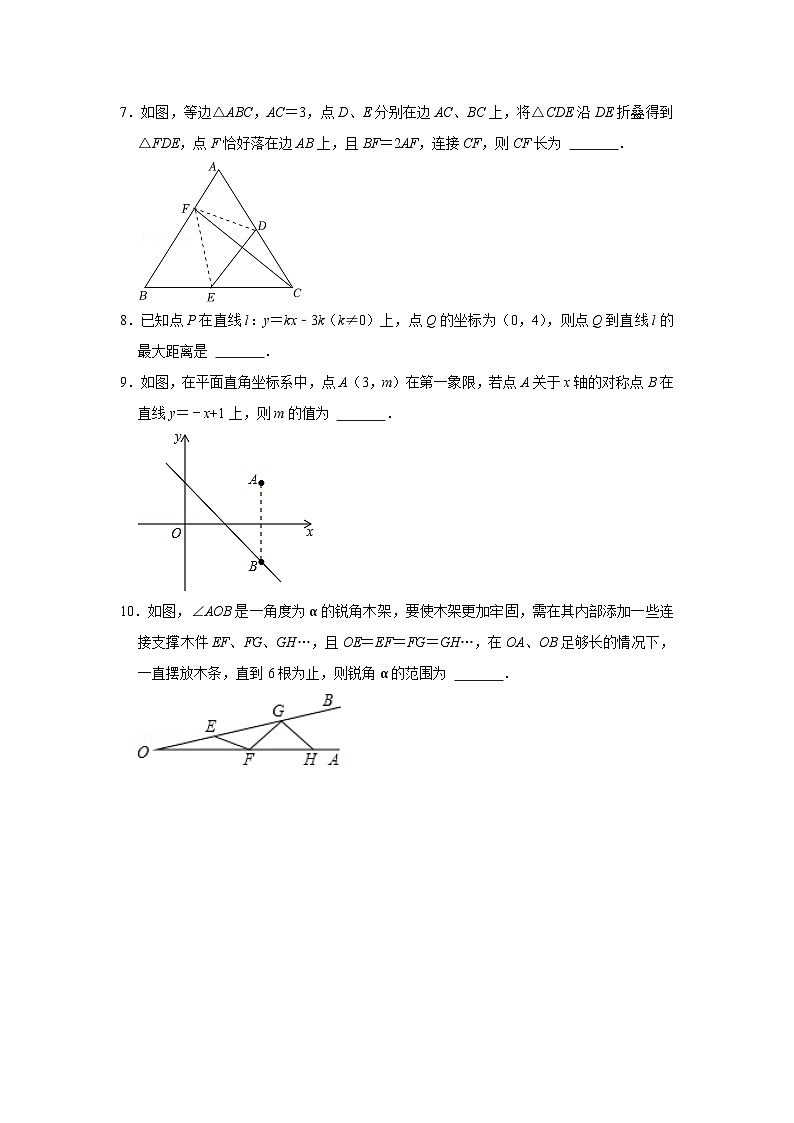
7．如图，等边△ABC，AC＝3，点D、E分别在边AC、BC上，将△CDE沿DE折叠得到△FDE，点F恰好落在边AB上，且BF＝2AF，连接CF，则CF长为 ．
8．已知点P在直线l：y＝kx﹣3k（k≠0）上，点Q的坐标为（0，4），则点Q到直线l的最大距离是 ．
9．如图，在平面直角坐标系中，点A（3，m）在第一象限，若点A关于x轴的对称点B在直线y＝﹣x+1上，则m的值为 ．
10．如图，∠AOB是一角度为α的锐角木架，要使木架更加牢固，需在其内部添加一些连接支撑木件EF、FG、GH…，且OE＝EF＝FG＝GH…，在OA、OB足够长的情况下，一直摆放木条，直到6根为止，则锐角α的范围为 ．
三．解答题（共4小题）
11．如图，直线l1的函数表达式为y1＝﹣3x+3，l1与x轴交于点B，直线l2：y2＝kx+b经过点A（4，0），l1与l2交点C（a，﹣3）．
（1）求直线l2的函数表达式；
（2）观察图象，当x满足 时，y1＞y2；
（3）点M为y轴上一点，若MB+MC的值最小，则点M的纵坐标为 ；
（4）点P在直线l2上，若满足S△ABP＝2S△ABC，求点P的坐标．
12．某容器有一个进水管和一个出水管，从某时刻开始的前4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水．已知进水管进水的速度与出水管出水的速度是两个常数，容器内水量y（升）与时间x（分钟）之间的关系如图所示．
（1）求进水管的进水速度；
（2）当4＜x≤12时，求y关于x的函数关系式；
（3）关闭进水管后，再经过 分钟能放空容器中的水．
13．四边形ABCD若满足∠A+∠C＝180°，则我们称该四边形为“对角互补四边形”．
（1）四边形ABCD为对角互补四边形，且∠B：∠C：∠D＝2：3：4，则∠A的度数为 ；
（2）如图1，四边形ABCD为对角互补四边形，∠BAD＝∠BCD＝90°，AB＝AD．
求证：AC平分∠BCD．
小云同学是这么做的：延长CD至M，使得DM＝BC，连AM，可证明△ABC≌△ADM，得到△ACM是等腰直角三角形，由此证明出AC平分∠BCD，还可以知道CB、CD、CA三者关系为： ；
（3）如图2，四边形ABCD为对角互补四边形，且满足∠BAD＝60°，AB＝AD，试证明：
①AC平分∠BCD；
②CA＝CB+CD；
（4）如图3，四边形ABCD为对角互补四边形，且满足∠ABC＝60°，AD＝CD，则BA、BC、BD三者关系为： ．
14．对于平面直角坐标系xOy中的点A和点P，若将点P绕点A顺时针旋转90°后得到点Q，则称点Q为点P关于点A的“顺转点”，图1为点P关于点A的“顺转点”Q的示意图．
【知识理解】
（1）已知点A的坐标为（0，0），点P关于点A的“顺转点”为点Q．
①若点P的坐标为（1，0），则点Q的坐标为 ；
②当点P的坐标为 时，点Q的坐标为（2，﹣1）；
③△PAQ是 三角形；
【知识运用】
（2）如图2，已知直线y=12x+1与x轴交于点A．
①点B的坐标为（1，0），点C在直线y=12x+1上，若点C关于点B的“顺转点”在坐标轴上，则点C的坐标为 ；
②点E在直线y=12x+1上，点E关于点A的“顺转点”为点F，则直线AF的表达式为 ；
【知识迁移】
（3）如图3，已知直线l1：y＝﹣2x+2与y轴交于点A，直线l2经过点A，l1与l2在A点相交所形成的夹角为45°，则直线l2的函数表达式为 ；
（4）点A是平面直角坐标系内一点，点P（2，0）关于点A的“顺转点”为点B，点B恰好落在直线y＝﹣x上．当线段AP最短时，点A的坐标为 ．
参考答案与试题解析
一．选择题（共5小题）
1．【解答】解：∵AB＝AC，AD⊥BC，
∴BD＝DC=12BC，
∵BD=2，
∴BC＝22，
∵BE⊥AC，∠BAC＝45°，
∴BE＝AE，
∵∠C+∠EAF＝90°，∠C+∠EBC＝90°，
∴∠EAF＝∠EBC，
在△EAF和△EBC中，
∠AEF=∠BEC=90°AE=BE∠EAF=∠EBC，
∴△EAF≌△EBC（ASA），
∴AF＝BC＝22，
故选：D．
2．【解答】解：连接DE，
∵∠ABC＝∠ADC＝90°，点E是AC的中点，
∴点A，B，C，D在以E为圆心，AC为直径的同一个圆上，
∵∠BAD＝70°，
∴∠DEB＝2∠BAD＝140°，
∵DE＝BE=12AC，
∴∠EBD＝∠EDB=180°−140°2=20°，
故选：A．
3．【解答】解：由图象可得，
乙晚出发1小时，故选项A正确；
乙出发3﹣1＝2小时追上甲，故选项B错误；
甲的速度是12÷3＝4（千米/小时），故选项C正确；
乙先到达B地，故选项D正确；
故选：B．
4．【解答】解：如图，取BC的中点G，连接MG，
∵旋转角为60°，
∴∠MBH+∠HBN＝60°，
又∵∠MBH+∠MBC＝∠ABC＝60°，
∴∠HBN＝∠GBM，
∵CH是等边△ABC的对称轴，
∴HB=12AB，
∴HB＝BG，
又∵MB旋转到BN，
∴BM＝BN，
在△MBG和△NBH中，
BG=BH∠MBG=∠NBHMB=NB，
∴△MBG≌△NBH（SAS），
∴MG＝NH，
根据垂线段最短，MG⊥CH时，MG最短，即HN最短，
此时∵∠BCH=12×60°＝30°，CG=12AB=12×5=52，
∴MG=12CG=54，
∴HN=54，
故选：A．
5．【解答】解：由勾股定理得正方形的对角线BC长度为2．
∴BM＝BC=2，
∴点M表示的数为：1−2．
故选：C．
二．填空题（共5小题）
6．【解答】解：把y＝1代入y＝﹣x得，x＝﹣1，
根据图象可得：关于x的不等式﹣x＜kx+b的解集为：x＞﹣1，
故答案为：x＞﹣1．
7．【解答】解：过F作FH⊥BC于H，如图：
∵△ABC是等边三角形，
∴∠B＝60°，AB＝BC＝AC＝3，
∵BF＝2AF，
∴BF=23AB＝2，
在Rt△BFH中，∠BFH＝90°﹣∠FBH＝30°，
∴BH=12BF＝1，FH=3BH=3，
∴CH＝BC﹣BH＝3﹣1＝2，
在Rt△CFH中，CF=FH2+CH2=(3)2+22=7，
故答案为：7．
8．【解答】解：∵直线l：y＝kx﹣3k＝k（x﹣3），
∴直线l一定过点（3，0），
∵点P在直线l：y＝kx﹣3k（k≠0）上，
∴P（3，0），
过点Q作直线l的所有垂线中，PQ是点Q到直线l的最大距离，
∵点Q的坐标为（0，4），
∴PQ=32+42=5，
∴点Q到直线l的最大距离是5，
故答案为：5．
9．【解答】解：∵点A（3，m），
∴点A关于x轴的对称点B（3，﹣m），
∵B在直线y＝﹣x+1上，
∴﹣m＝﹣3+1＝﹣2，
∴m＝2，
故答案为：2．
10．【解答】解：∵OE＝EF，∠AOB＝α，
∴∠EFO＝α，
∵∠GEF是△OEF的外角，
∴∠GEF＝2α，
∵EF＝FG，
∴∠EGF＝∠GEF＝2α，
∵∠GFH是△OGF的外角，
∴∠GFH＝∠O+∠EGF＝3α，
综上所述，添加一根木件，三角形的外角为2α；
添加两根木件，三角形的外角为3α；
……
∴添加6根木件，三角形的外角为7α，
∵等腰三角形的底角必须是锐角，
∴7α≥90°6α＜90°，
∴（907）°≤α＜15°．
故答案为：（907）°≤α＜15°．
三．解答题（共4小题）
11．【解答】解：（1）∵直线l1：y1＝﹣3x+3过点C（a，﹣3），
∴﹣3＝﹣3a+3，
∴a＝2，
∴C（2，﹣3），
∵直线l2：y2＝kx+b经过点A（4，0），C，
∴4k+b=02k+b=−3，解得k=32b=−6，
∴直线l2的函数表达式为y=32x﹣6；
（2）观察图象，当x满足x＜2时，y1＞y2；
故答案为：x＜2；
（3）在直线l1：y1＝﹣3x+3中，令y＝0，则﹣3x+3＝0，
∴x＝1，
∴B（1，0），
∴B关于y轴的对称点B′（﹣1，0），
连接B′C，交y轴于点M，此时，MB+MC的值最小，
设直线B′C的解析式为y＝mx+n，
则−m+n=02m+n=−3，解得m=−1n=−1，
∴直线B′C的解析式为y＝﹣x﹣1，
当x＝0时，y＝﹣1，
∴M（0，﹣1）；
故答案为：（0，﹣1）；
（4）∵点A（4，0），B（1，0），C（2，﹣3），
∴AB＝4﹣1＝3，
∴S△ABC=12×3×3=92，
∵S△ABP＝2S△ABC，
∴S△ABP=12×3×|yP|=9，
∴|yP|＝6，
∴yP＝±6，
当y＝6时，代入y=32x﹣6得，6=32x﹣6，
解得x＝8，
∴P（8，6）；
当y＝﹣6时，代入y=32x﹣6得，﹣6=32x﹣6，
解得x＝0，
∴P（0，﹣6），
综上，点P的坐标为（8，6）或（0，﹣6）．
12．【解答】解：（1）根据图象得：每分钟进水20÷4＝5（升）；
答：进水管的进水速是每分钟5升；
（2）当4＜x≤12时，设y关于x的函数关系式为y＝kx+b，
∵图象过（4，20）、（12，30），
∴4k+b=2012k+b=30，解得k=54b=15，
∴y=54x+15；
（3）由图象可得，每分钟的出水量为20+(12−4)×5−3012−4=154（升），
∴关闭进水管后，再经过30÷154=8分钟能放空容器中的水，
故答案为：8．
13．【解答】解：（1）∵四边形ABCD为对角互补四边形，
∴∠B+∠D＝180°，
∵∠B：∠C：∠D＝2：3：4，
∴∠B＝180°×13=60°，
∴∠C＝90°，
∴∠A＝90°，
故答案为：90°；
（2）∵△ABC≌△ADM，
∴AC＝AM，BC＝DM，
∵△ACM是等腰直角三角形，
∴CM=2AC，
∵CM＝CD+DM，
∴CM＝CD+BC=2AC，
故答案为：CD+BC=2AC；
（3）①延长CD至M，使DM＝BC，连接AM，
∵四边形ABCD为对角互补四边形，
∴∠B+∠ADC＝180°，
∴∠ADM＝∠B，
∵AB＝AD，
∴△ABC≌△ADM（SAS），
∴AC＝AM，∠BAC＝∠CAM，
∵∠BAD＝60°，
∴∠CAM＝60°，
∴△ACM是等边三角形，
∴∠ACM＝∠M＝60°，
∵∠ACB＝∠M，
∴∠ACB＝60°，
∴∠ACB＝∠ACM，
∴AC平分∠BCD；
②∵AC＝CM，BC＝DM，
∴CM＝CD+DM＝CD+BC，
∴AC＝CD+BC；
（4）延长BC至M，使CM＝AB，连接DM，
∵四边形ABCD为对角互补四边形，
∴∠A+∠BCD＝∠BCD+∠DCM＝180°，
∴∠A＝∠DCM，
∵AD＝CD，
∴△ADB≌△CDM（SAS），
∴BD＝MD，∠ADB＝∠CDM，
∵∠ABC＝60°，
∴∠ADC＝120°，
∴∠BDM＝120°，
∴∠M＝∠DBM＝30°，
过点D作DN⊥BM交于点N，
∴N为BM的中点，
∴BM＝2MN，
在Rt△DNM中，MN=32DM=32BD，
∴BM=3BD，
∵BM＝BC+CM＝BC+AB=3BD，
故答案为：BC+AB=3BD．
14．【解答】解：（1）①∵A（0，0），P（1，0），点P关于点A的“顺转点”为点Q，
∴AP＝AQ，∠PAQ＝90°，
∴Q（0，﹣1），
故答案为：（0，﹣1）；
②如图1，过点P作PE⊥y轴交于点E，过点Q作QF⊥y轴交于点F，
∵∠PAQ＝90°，
∴∠EPA+∠FAQ＝90°，
∵∠EPA+∠EAP＝90°，
∴∠FAQ＝∠EAP，
∵AP＝AQ，
∴△APE≌△QAF（AAS），
∴AF＝EP，AE＝FQ，
∵Q（2，﹣1），
∴AF＝1，FQ＝2，
∴EP＝1，AE＝2，
∴P（1，2），
故答案为：（1，2）；
③∵AP＝AQ，∠PAQ＝90°，
∴△PAQ是等腰直角三角形，
故答案为：等腰直角；
（2）①设点C关于点B的“顺转点”为D，
当D点在x轴坐标轴时，BC⊥x轴，
∵B（1，0），点C在直线y=12x+1上，
∴C（1，32）；
如图2，当D点在y轴正半轴时，
过点B作HG⊥x轴，过点D作DG⊥y轴交GH于点G，过点C作CH⊥y轴交GH于点H，
∵∠DBC＝90°，
∴∠DBG+∠CBH＝90°，
∵∠DBG+∠GDB＝90°，
∴∠CBH＝∠GDB，
∵BD＝BC，
∴△BDG≌△CBH（AAS），
∴DG＝BH，BG＝CH，
∵B（1，0），
∴DG＝BH＝1，
∴C点纵坐标为﹣1，
∵点C在直线y=12x+1上，
∴C（﹣4，﹣1）；
综上所述：C点坐标为（1，32）或（﹣4，﹣1）；
故答案为：（1，32）或（﹣4，﹣1）；
②如图3，设E（t，12t+1），
过点A作GH⊥x轴，过点E作EG⊥GH交于点G，过点F作FH⊥GH交于点H，
∵∠EAF＝90°，
∴∠EAG+∠HAF＝90°，
∵∠GAE+∠GEA＝90°，
∴∠HAF＝∠GEA，
∵AE＝AF，
∴△AGE≌△FHA（AAS），
∴AG＝HF，GE＝AH，
∵A（﹣2，0），
∴GE＝t+2＝AH，AG=12t+1＝HF，
∴F（12t﹣1，﹣t﹣2），
设直线AF的解析式为y＝kx+b，
∴−2k+b=0(12t−1)k+b=−t−2，
∴k=−2b=−4，
∴y＝﹣2x﹣4，
故答案为：y＝2x﹣4；
（3）令x＝0，则y＝2，
∴A（0，2），
如图4，设l1与x轴的交点为B，l2与x轴的交点为C，过点C作CD⊥l1交于点D，
∴B（1，0），
∵∠BAC＝45°，
∴∠ACD＝45°，
∴AD＝CD，
在Rt△AOC中，∠OAB+∠ACO＝45°，
∴∠BCD＝∠AOB，
∵tan∠BAO=12，
∴BDCD=12，
∴CD＝2BD，
∵AB=5，
∴5+BD＝2BD，
∴BD=5，
∴CD＝25，
∴BC＝5，
∴OC＝6，
∴C（6，0），
设直线AC的解析式为y＝kx+b，
∴6k+b=0b=2，
∴k=−13b=2，
∴y=−13x+2，
故答案为：y=−13x+2；
（4）设点A（x，y），B（m，﹣m），
如图5，过点A作MN∥x轴，过点P作PN⊥x轴交MN于点N，过点B作MB⊥x轴交MN于点M，
∵∠PAB＝90°，
∴∠MAB+∠NAP＝90°，
∵∠MAB+∠MBA＝90°，
∴∠NAP＝∠MBA，
∵AB＝AP，
∴△ABM≌△PAN（AAS），
∴AN＝MB，AM＝PN，
∴y＝x﹣m，2﹣x＝y+m，
∴x＝1，
∴A（1，y），
∴AP=1+y2≥1，
∴当y＝0时，AP最短，
∴A（1，0），
故答案为：（1，0）．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/11/28 16:33:23