备战2025年高考数学二轮复习课件专题4立体几何培优拓展（11）截面与交线问题

这是一份备战2025年高考数学二轮复习课件专题4立体几何培优拓展（11）截面与交线问题，共28页。PPT课件主要包含了解析如图所示等内容，欢迎下载使用。
立体几何中,截面是指用一个平面去截几何体得到的平面图形,确定截面的形状及内含的数量关系,首先要确定交线.“截面、交线”问题是高考中对立体几何知识考查的最具创新性的题型之一,它渗透了一些动态的线、面等元素,给静态的立体几何题赋予了活力.求截面、交线问题常与解三角形、多边形面积、扇形弧长及面积、平面的基本性质等结合,有些问题还要借助于空间向量坐标运算求解.
角度一 多面体中的截面问题
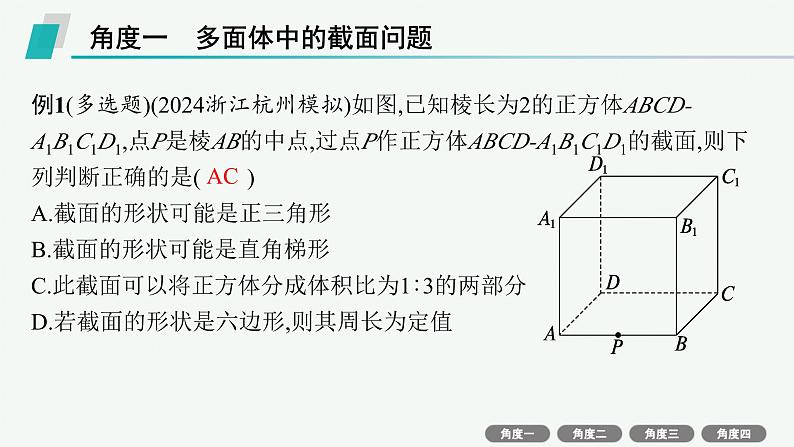
例1(多选题)(2024浙江杭州模拟)如图,已知棱长为2的正方体ABCD-A1B1C1D1,点P是棱AB的中点,过点P作正方体ABCD-A1B1C1D1的截面,则下列判断正确的是(　　)A.截面的形状可能是正三角形B.截面的形状可能是直角梯形C.此截面可以将正方体分成体积比为1∶3的两部分D.若截面的形状是六边形,则其周长为定值
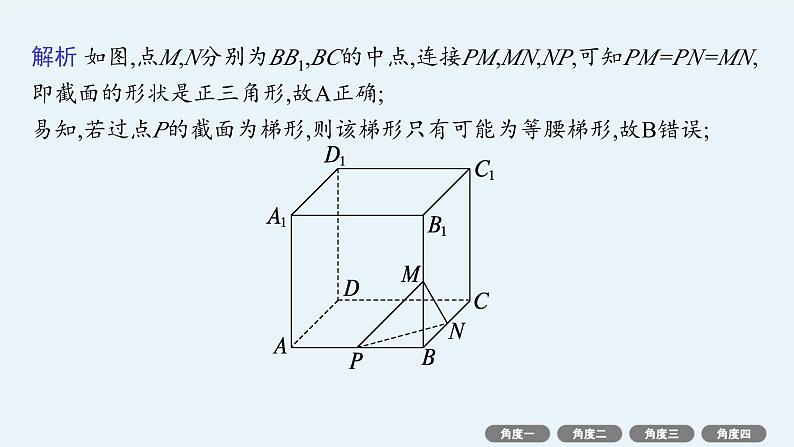
解析 如图,点M,N分别为BB1,BC的中点,连接PM,MN,NP,可知PM=PN=MN,即截面的形状是正三角形,故A正确;易知,若过点P的截面为梯形,则该梯形只有可能为等腰梯形,故B错误;
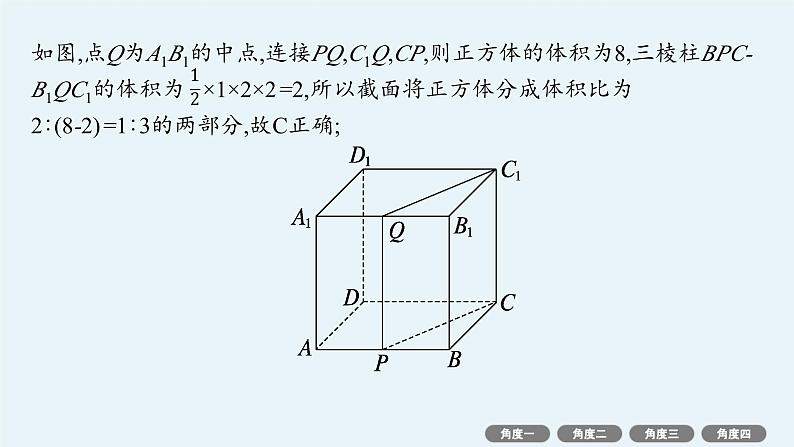
如图,点Q为A1B1的中点,连接PQ,C1Q,CP,则正方体的体积为8,三棱柱BPC-B1QC1的体积为 ×1×2×2=2,所以截面将正方体分成体积比为2∶(8-2)=1∶3的两部分,故C正确;
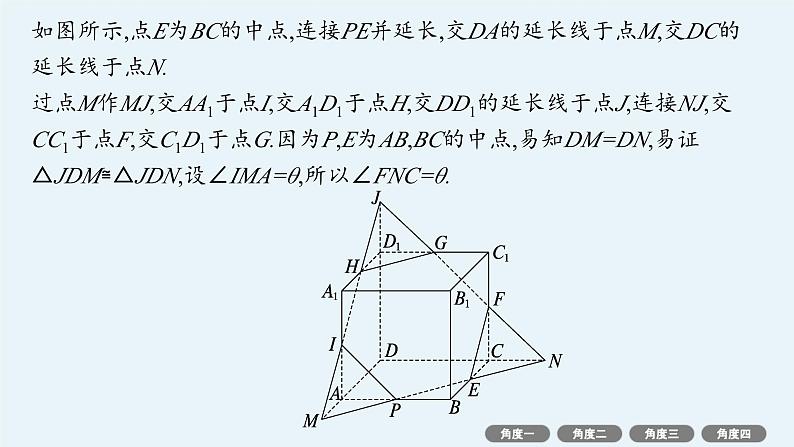
如图所示,点E为BC的中点,连接PE并延长,交DA的延长线于点M,交DC的延长线于点N.过点M作MJ,交AA1于点I,交A1D1于点H,交DD1的延长线于点J,连接NJ,交CC1于点F,交C1D1于点G.因为P,E为AB,BC的中点,易知DM=DN,易证△JDM≌△JDN,设∠IMA=θ,所以∠FNC=θ.
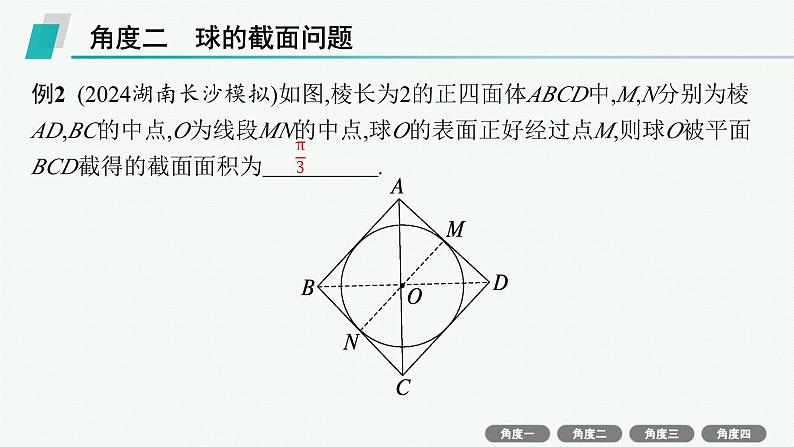
角度二 球的截面问题
例2 (2024湖南长沙模拟)如图,棱长为2的正四面体ABCD中,M,N分别为棱AD,BC的中点,O为线段MN的中点,球O的表面正好经过点M,则球O被平面BCD截得的截面面积为　　　　　. 
解析 如图,在棱长为2的正四面体ABCD中,连接AN,DN,过O作OE⊥DN于点E.因为点M,N分别为棱AD,BC的中点,所以AN⊥BC,DN⊥BC.又AN∩DN=N,AN,DN⊂平面AND,所以BC⊥平面AND.又BC⊂平面BCD,于是平面AND⊥平面BCD.又平面AND∩平面BCD=DN,OE⊥DN,所以OE⊥平面BCD.由题可知AN=DN= ,DM=1,MN⊥AD,所以MN= ,
角度三 多面体中的交线问题
例3在正三棱台A1B1C1-ABC中,A1B1=1,AB=AA1=2,点E,F分别为棱BB1,A1C1的中点,若过点A,E,F作截面,则截面与上底面A1B1C1的交线长为　　　　. 
解析 连接AF并延长交CC1的延长线于点M,连接ME交B1C1于点N,连接FN,如图,则线段FN即为截面AEF与上底面ABC的交线.
角度四 与球有关的交线问题
例4已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心, 为半径的球面与侧面BCC1B1的交线长为　　　　　. 
解析 如图所示,∵∠B1C1D1=∠B1A1D1=∠BAD=60°且B1C1=C1D1,∴△B1C1D1为等边三角形.∴B1D1=2.设点O1是B1C1的中点,则O1D1= ,易证D1O1⊥平面BCC1B1,设P是球面与侧面BCC1B1交线上任意一点,连接O1P,则O1D1⊥O1P,取BB1,CC1的中点分别为E,F,则B1E=C1F=O1B1=O1C1=1,EF=2,∴O1E=O1F= ,O1E2+O1F2=EF2=4,∴∠EO1F=90°,
针对训练1.(2024河北廊坊模拟)如图所示,在正四棱台ABCD-A1B1C1D1中,上底面边长为3,下底面边长为6,体积为 ,点E在AD上且满足DE=2AE,过点E的平面α与平面D1AC平行,且与正四棱台各面相交得到截面多边形,则该截面多边形的周长为(　　)
又ME∩MN=M,ME,MN⊂平面EMN,AD1∩CD1=D1,AD1,CD1⊂平面D1AC,所以平面EMN∥平面D1AC,所以△EMN即为所求截面多边形,所以截面多边形的周长为 故选D.
2.已知正三棱柱ABC-A1B1C1的各棱长均为2,D为棱AB的中点,则过点D的平面截该三棱柱外接球所得截面面积的取值范围为　　　　　. 
解析 如图,正三棱柱ABC-A1B1C1的外接球的球心O为上、下底面的外接圆圆心的连线O1O2的中点,连接AO2,AO,OD.设外接球的半径为R,下底面外接圆的半径为r.
3.(2024湖南长沙模拟)如图,已知在正三棱柱ABC-A1B1C1中,AA1=AB=2,且点E,F分别为棱BB1,A1C1的中点.过点A,E,F作三棱柱截面交C1B1于点P,则线段B1P的长度为　　　　　. 
解析 如图,延长AF,交CC1的延长线于点M,连接EM,交B1C1于点P,则四边形AFPE即为所求截面多边形.因为三棱柱ABC-A1B1C1为正三棱柱,AA1=AB=2,点F为棱A1C1的中点,所以△AFA1≌△MFC1,所以MC1=AA1=2.
4.(2024江苏南京模拟)在正三棱锥A-BCD中,底面△BCD的边长为4,E为AD的中点,AB⊥CE,则以D为球心,AD为半径的球截该棱锥各面所得交线长为　　　　. 
解析 如图,取CD中点F,连接BF,过点A作AO⊥平面BCD,垂足为O.由正三棱锥性质可知,点O为正三角形BCD的中心,所以点O在BF上.因为CD⊂平面BCD,所以AO⊥CD.又BF⊥CD,BF∩AO=O,BF,AO⊂平面ABO,所以CD⊥平面ABO.又AB⊂平面ABO,所以AB⊥CD.又CE⊥AB,CE∩CD=C,CE,CD⊂平面ACD,所以AB⊥平面ACD.又AC⊂平面ACD,所以AC⊥AB.由正三棱锥性质可知,AC,AB,AD两两垂直,且AB=AC=AD,则