九年级下册29.3 课题学习 制作立体模型完整版教学课件ppt

这是一份九年级下册29.3 课题学习 制作立体模型完整版教学课件ppt，文件包含293课题学习制作立体模型课件pptx、293课题学习制作立体模型教案docx、29章投影与视图单元整理分析教案docx等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
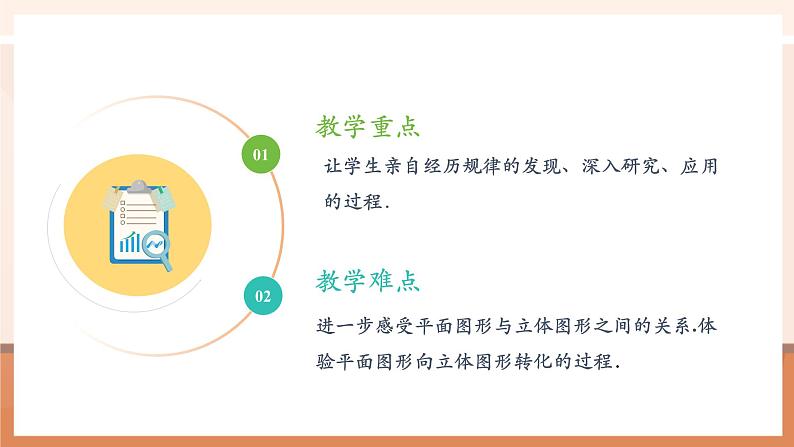
让学生亲自经历规律的发现、深入研究、应用的过程．学生通过手工制作实现理论与实践的结合；在探索解决实际问题的过程中，养成科学的研究态度．进一步感受平面图形与立体图形之间的关系.体验平面图形向立体图形转化的过程．
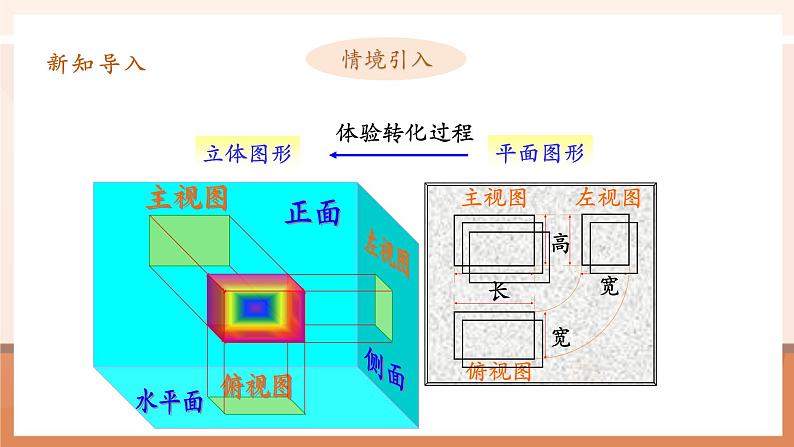
1、体验平面图形向立体图形转化的过程.2、体会用三视图表示立体图形的作用.3、进一步感受平面图形与立体图形之间的关系.
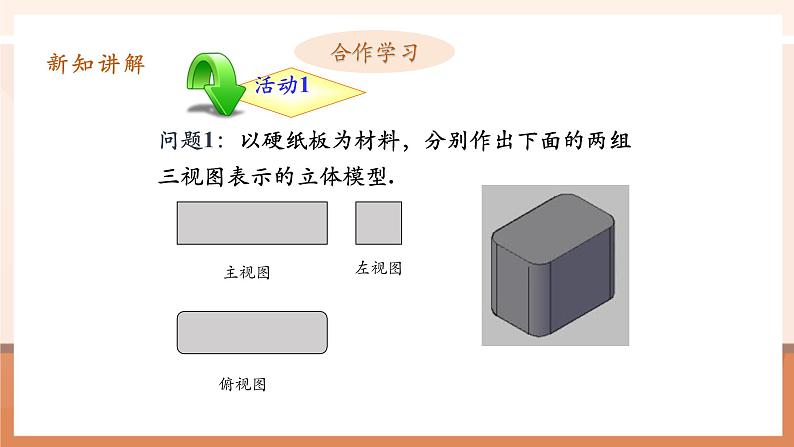
问题1：以硬纸板为材料，分别作出下面的两组三视图表示的立体模型.
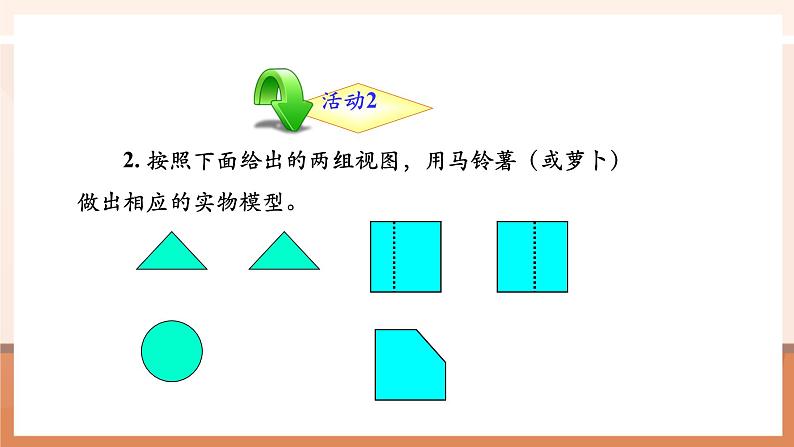
2. 按照下面给出的两组视图，用马铃薯（或萝卜）做出相应的实物模型。
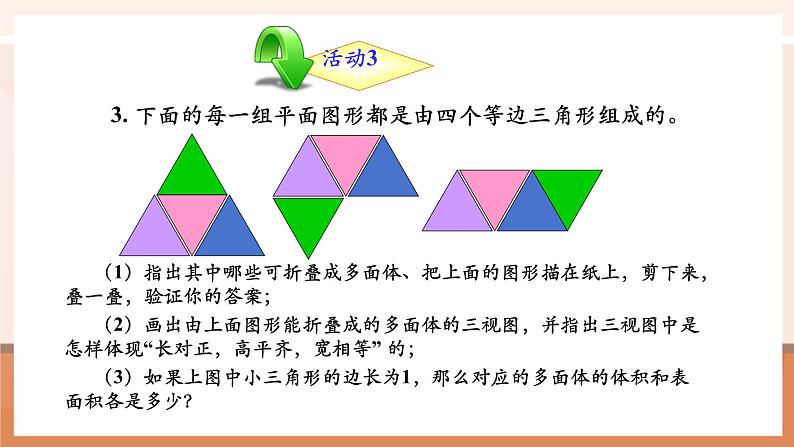
3. 下面的每一组平面图形都是由四个等边三角形组成的。
（1）指出其中哪些可折叠成多面体、把上面的图形描在纸上，剪下来，叠一叠，验证你的答案； （2）画出由上面图形能折叠成的多面体的三视图，并指出三视图中是怎样体现“长对正，高平齐，宽相等” 的； （3）如果上图中小三角形的边长为1，那么对应的多面体的体积和表面积各是多少？
1. 数学是以数量关系和空间形式为主要研究对象的科学，数量关系和空间形式是从现实世界中抽象出来的。 很明显，关于投影和视图的知识是从实际需要（建筑、制造等）中产生的，它们与实际模型联系得非常紧密。 2. 感性认识需要上升为理性认识，理论指导下的实践会更明确有效。
例：下面的图形是由一个扇形和一个圆组成.(1)把下面的图形描在纸上，剪下来，组成一个圆锥，画出这个圆锥的三视图.
(2)如果图中扇形半径为13，圆的半径为5，那么对应圆锥的体积是多少？
1.下列四组图中，每组左边的平面图形能够折叠成右边的立体图形的是（ ）A.①② B.①④C.② D.③
2.由6个大小相同的正方体搭成的几何体如图1所示，则关于它的视图说法正确的是（ ） A．正视图的面积最大 B．左视图的面积最大C．俯视图的面积最大 D．三个视图的面积一样大
3．如图 是一个几何体的三视图，画出这个几何体的形状.
4.某工厂要加工一批密封罐，设计者给出了密封罐的三视图(如图).请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位：mm).
由三视图可知，密封罐的形状是正六棱柱(如图1).密封罐的高为50 mm，底面正六边形的直径为100mm，边长为50 mm， 图2是它的展开图.
由展开图可知，制作一个密封罐所需钢板的面积为
1.如图是某工件的三视图，则此工件的表面积为(　　)A．15π cm2　　　B．51π cm2C．66π cm2　　　D．24π cm2
2.某工厂加工一批无底帐篷，设计者给出了帐篷的三视图请你按照三视图确定每顶帐篷的表面积(图中尺寸单位：cm).
S锥侧＝π·150·240＝36 000π(cm2),S柱侧＝2π·150·200＝60 000π(cm2)，∴S表＝S锥侧＋S柱侧＝36 000π＋60 000π ＝96 000π(cm2)＝9.6π m2.
3.如图是某个几何体的展开图，（1）请根据展开图选择纸板、小剪刀、透明胶等制作例题模型。（2）若中间的矩形长为20 cm，宽为20cm,上面扇形的中心角为2400.试求该几何体的表面积及体积。
解：(1)立体模型如图所示：　
先根据三视图判断几何体的形状和基本的数据、特征再进行制止