2024-2025学年上学期初中数学人教版（2024）七年级期末必刷常考题之解一元一次方程练习

这是一份2024-2025学年上学期初中数学人教版（2024）七年级期末必刷常考题之解一元一次方程练习，共15页。试卷主要包含了定义运算等内容，欢迎下载使用。
1．（2024秋•琼山区校级期中）若代数式x+1的值为3，则x等于（ ）
A．4B．﹣4C．2D．﹣2
2．（2024秋•越秀区校级期中）如果a、b是定值，且关于x的方程2kx+a3=2+x+bk6，无论k为何值时，它的解总是x＝1，那么2a+b的值是（ ）
A．15B．16C．17D．18
3．（2024秋•长沙期中）下列方程的变形正确的是（ ）
A．由4x+3＝8x+7，得4x﹣8x＝3﹣7
B．由﹣8x+3＝﹣13x﹣7，得﹣8x+13x＝﹣7﹣3
C．由3x﹣2＝2x﹣1，得3x﹣2x＝1+2
D．由﹣5x﹣7＝2x﹣11，得11﹣7＝2x﹣5x
4．（2023秋•通榆县期末）已知x＝2是方程3x﹣5＝2x+m的解，则m的值是（ ）
A．1B．﹣1C．3D．﹣3
5．（2024春•射洪市期末）解方程x+12−2x−36=1去分母正确的是（ ）
A．3（x+1）﹣2x﹣3＝6B．3（x+1）﹣2x﹣3＝1
C．3（x+1）﹣（2x﹣3）＝12D．3（x+1）﹣（2x﹣3）＝6
二．填空题（共5小题）
6．（2024秋•昆明期中）已知关于x的方程2x+m＝0的解是x＝﹣3，则m的值为 ．
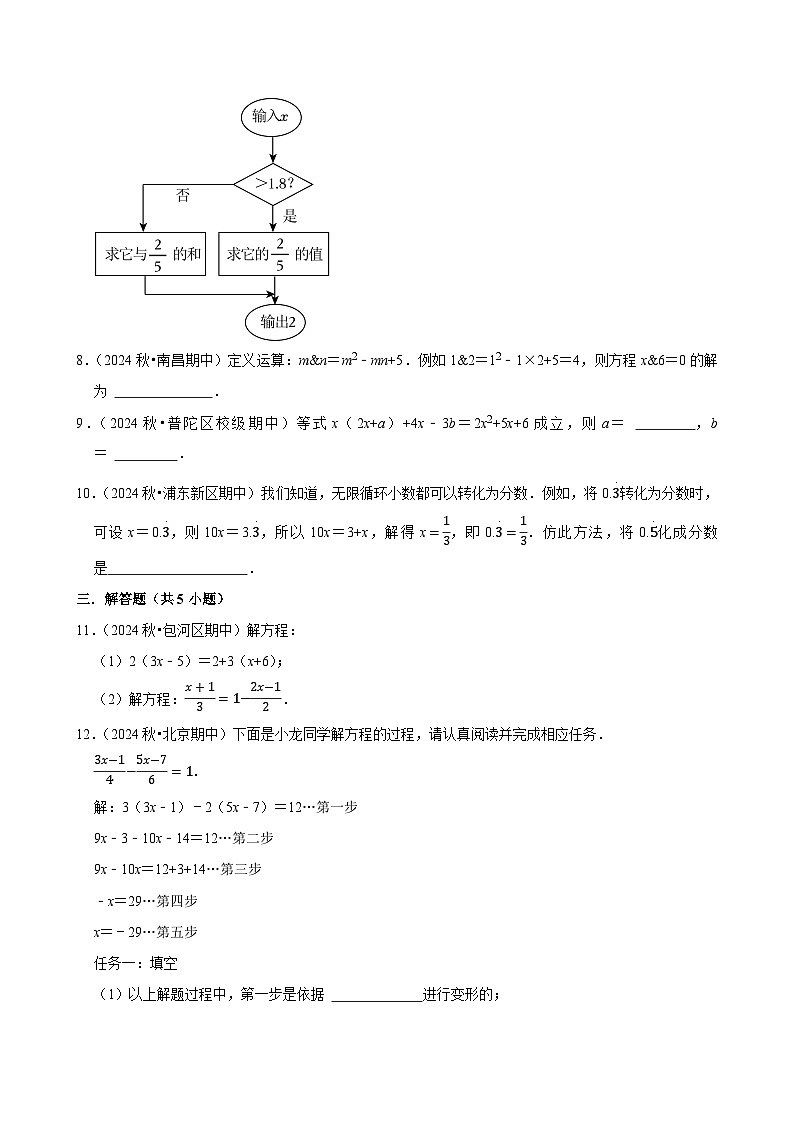
7．（2024秋•宝山区期中）如图所示是一个计算流程图，若输出数是2，则输入x的值为 ．
8．（2024秋•南昌期中）定义运算：m&n＝m2﹣mn+5．例如1&2＝12﹣1×2+5＝4，则方程x&6＝0的解为 ．
9．（2024秋•普陀区校级期中）等式x（2x+a）+4x﹣3b＝2x2+5x+6成立，则a＝ ，b＝ ．
10．（2024秋•浦东新区期中）我们知道，无限循环小数都可以转化为分数．例如，将0.3⋅转化为分数时，可设x＝0.3⋅，则10x＝3.3⋅，所以10x＝3+x，解得x=13，即0.3⋅=13．仿此方法，将0.5⋅化成分数是 ．
三．解答题（共5小题）
11．（2024秋•包河区期中）解方程：
（1）2（3x﹣5）＝2+3（x+6）；
（2）解方程：x+13=1−2x−12．
12．（2024秋•北京期中）下面是小龙同学解方程的过程，请认真阅读并完成相应任务．
3x−14−5x−76=1．
解：3（3x﹣1）﹣2（5x﹣7）＝12…第一步
9x﹣3﹣10x﹣14＝12…第二步
9x﹣10x＝12+3+14…第三步
﹣x＝29…第四步
x＝﹣29…第五步
任务一：填空
（1）以上解题过程中，第一步是依据 进行变形的；
（2）第 步开始出现错误，这一步的错误的原因是 ；
任务二：请你求出方程正确的解．
13．（2024秋•北京期中）小涵在解关于x的一元一次方程3x−12+□=3时，发现正整数“□”被污染了，于是就去问同学小李，小李也记不清“□”的具体值了，只记得这个方程的解是正整数．小涵经过深入思考，想出了一个好办法，她将“□”设为m，通过计算，很快得到了□的值．你知道她是怎么计算的吗？请你求出□的值．
14．（2024秋•东城区校级期中）对于有理数a，b，定义了一种“⊗”的新运算，具体为：a⊗b=2a−b(a≥b)a−23b(a＜b)．
（1）计算：
①2⊗1；
②（﹣4）⊗（﹣3）．
（2）若x＝2是关于x的一元一次方程3⊗m＝﹣1+3x的解，求m的值．
15．（2024秋•肇州县校级期中）a是最大的负整数，且a﹣2b＝﹣13，则关于x的一元一次方程x+a5−1=x−b2的解是多少？
2024-2025学年上学期初中数学人教版（2024）七年级期末必刷常考题之解一元一次方程
参考答案与试题解析
一．选择题（共5小题）
1．（2024秋•琼山区校级期中）若代数式x+1的值为3，则x等于（ ）
A．4B．﹣4C．2D．﹣2
【考点】解一元一次方程；代数式求值．
【专题】一次方程（组）及应用；运算能力．
【答案】C
【分析】由题意易得一元一次方程，解方程即可求解．
【解答】解：由题意得x+1＝3，
解得x＝2．
故选：C．
【点评】本题主要考查解一元一次方程，代数式求值，掌握解一元一次方程的步骤是关键．
2．（2024秋•越秀区校级期中）如果a、b是定值，且关于x的方程2kx+a3=2+x+bk6，无论k为何值时，它的解总是x＝1，那么2a+b的值是（ ）
A．15B．16C．17D．18
【考点】一元一次方程的解．
【专题】一次方程（组）及应用；运算能力．
【答案】C
【分析】先将x＝1代入方程2kx+a3=2+x+bk6，整理得（4﹣b）k＝13﹣2a，再根据无论k为何值时，该方程的解总是x＝1得4﹣b＝0，13﹣2a＝0，进而得b＝4，2a＝13，由此可得2a+b的值．
【解答】解：将x＝1代入方程2kx+a3=2+x+bk6，得2k+a3=2+1+bk6，
将2k+a3=2+1+bk6的两边同时乘以6，得：4k+2a＝12+1+b，
整理得：（4﹣b）k＝13﹣2a，
∵关于x的方程2kx+a3=2+x+bk6，无论k为何值时，它的解总是x＝1，
∴4﹣b＝0，13﹣2a＝0，
∴b＝4，2a＝13，
∴2a+b＝17．
故选：C．
【点评】此题主要考查了一元一次方程的解，理解一元一次方程的解，以及一元一次方程有无数解的条件是解决问题的关键．
3．（2024秋•长沙期中）下列方程的变形正确的是（ ）
A．由4x+3＝8x+7，得4x﹣8x＝3﹣7
B．由﹣8x+3＝﹣13x﹣7，得﹣8x+13x＝﹣7﹣3
C．由3x﹣2＝2x﹣1，得3x﹣2x＝1+2
D．由﹣5x﹣7＝2x﹣11，得11﹣7＝2x﹣5x
【考点】解一元一次方程；等式的性质．
【专题】一次方程（组）及应用；运算能力．
【答案】B
【分析】根据等式的性质逐项判断即可．
【解答】解：A、由4x+3＝8x+7，得4x﹣8x＝7﹣3，原变形错误，故此选项不符合题意；
B、由﹣8x+3＝﹣13x﹣7，得﹣8x+13x＝﹣7﹣3，正确，故此选项符合题意；
C、由3x﹣2＝2x﹣1，得3x﹣2x＝﹣1+2，原变形错误，故此选项不符合题意；
D、由﹣5x﹣7＝2x﹣11，得11﹣7＝2x+5x，原变形错误，故此选项不符合题意；
故选：B．
【点评】本题考查了解一元一次方程，等式的性质，注意移项时要改变符号．
4．（2023秋•通榆县期末）已知x＝2是方程3x﹣5＝2x+m的解，则m的值是（ ）
A．1B．﹣1C．3D．﹣3
【考点】一元一次方程的解．
【专题】计算题；一次方程（组）及应用；运算能力．
【答案】D
【分析】把x＝2代入方程3x﹣5＝2x+m可得到关于m的方程，解方程可求得m的值．
【解答】解：∵x＝2是方程3x﹣5＝2x+m的解，
∴把x＝2代入方程可得6﹣5＝4+m，
解得m＝﹣3，
故选：D．
【点评】本题主要考查一元一次方程的解的定义，掌握方程的解满足方程是解题的关键．
5．（2024春•射洪市期末）解方程x+12−2x−36=1去分母正确的是（ ）
A．3（x+1）﹣2x﹣3＝6B．3（x+1）﹣2x﹣3＝1
C．3（x+1）﹣（2x﹣3）＝12D．3（x+1）﹣（2x﹣3）＝6
【考点】解一元一次方程．
【答案】D
【分析】这是一个带分母的方程，所以要先找出分母的最小公倍数，去分母即可．
【解答】解：由此方程的分母2，6可知，其最小公倍数为6，
故去分母得：3（x+1）﹣（2x﹣3）＝6．
故选：D．
【点评】去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．
二．填空题（共5小题）
6．（2024秋•昆明期中）已知关于x的方程2x+m＝0的解是x＝﹣3，则m的值为 6 ．
【考点】一元一次方程的解．
【专题】一次方程（组）及应用；运算能力．
【答案】6．
【分析】将x＝﹣3代入方程2x+m＝0之中即可得出m的值．
【解答】解：∵关于x的方程2x+m＝0的解是x＝﹣3，
∴2×（﹣3）+m＝0，
解得：m＝6．
故答案为：6．
【点评】此题主要考查了一元一次方程的解，理解一元一次方程的解的定义是解决问题的关键．
7．（2024秋•宝山区期中）如图所示是一个计算流程图，若输出数是2，则输入x的值为 5或1.6 ．
【考点】解一元一次方程．
【答案】5或1.6．
【分析】若x＞1.8，则25x=2，若x≤1.8，则x+25=2，分别解方程即可．
【解答】解：若x＞1.8，则25x=2，解得x＝5，适合题意；
若x≤1.8，则x+25=2，解得x＝1.6，适合题意；
综上，输入x的值为5或1.6，
故答案为：5或1.6．
【点评】本题考查了解一元一次方程，理解题意正确列出方程求解是解题的关键．
8．（2024秋•南昌期中）定义运算：m&n＝m2﹣mn+5．例如1&2＝12﹣1×2+5＝4，则方程x&6＝0的解为 x＝5或x＝1 ．
【考点】解一元一次方程．
【专题】一次方程（组）及应用；运算能力．
【答案】x＝5或x＝1．
【分析】把相应的值代入新定义的运算中，结合解一元一次方程的方法进行求解即可．
【解答】解：由题意得：x2﹣6x+5＝0，
（x﹣5）（x﹣1）＝0，
x﹣5＝0或x﹣1＝0，
解得：x＝5或x＝1．
故答案为：x＝5或x＝1．
【点评】本题主要考查解一元一次方程，解答的关键是对解一元一次方程的方法的掌握．
9．（2024秋•普陀区校级期中）等式x（2x+a）+4x﹣3b＝2x2+5x+6成立，则a＝ 1 ，b＝ ﹣2 ．
【考点】解一元一次方程；合并同类项．
【专题】一次方程（组）及应用；运算能力．
【答案】1，﹣2．
【分析】先去括号，再将所用项移到等号的左边并合并同类项，令各项系数为0列方程并求出a和b的值即可．
【解答】解：去括号，得2x2+ax+4x﹣3b＝2x2+5x+6，
移项、合并同类项，得（a﹣1）x﹣（3b+6）＝0，
∴a﹣1＝0，3b+6＝0，
∴a＝1，b＝﹣2．
故答案为：1，﹣2．
【点评】本题考查解一元一次方程、合并同类项，掌握合并同类项、一元一次方程的方法是解题的关键．
10．（2024秋•浦东新区期中）我们知道，无限循环小数都可以转化为分数．例如，将0.3⋅转化为分数时，可设x＝0.3⋅，则10x＝3.3⋅，所以10x＝3+x，解得x=13，即0.3⋅=13．仿此方法，将0.5⋅化成分数是 59 ．
【考点】解一元一次方程；有理数；等式的性质．
【专题】一次方程（组）及应用；运算能力．
【答案】见试题解答内容
【分析】根据题中的方法求出所求即可．
【解答】解：设x＝0.5⋅，则10x＝5.5⋅，
所以10x＝5+x，
解得：x=59．
故答案为：59．
【点评】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．
三．解答题（共5小题）
11．（2024秋•包河区期中）解方程：
（1）2（3x﹣5）＝2+3（x+6）；
（2）解方程：x+13=1−2x−12．
【考点】解一元一次方程．
【专题】一次方程（组）及应用；运算能力．
【答案】（1）x＝10；
（2）x=78．
【分析】（1）通过去括号、移项、合并同类项、系数化为1等过程，求得x的值；
（2）通过去分母、去括号、移项、合并同类项、系数化为1等过程，求得x的值．
【解答】解：（1）2（3x﹣5）＝2+3（x+6），
6x﹣10＝2+3x+18，
6x﹣3x＝2+18+10，
3x＝30，
x＝10；
（2）x+13=1−2x−12，
2（x+1）＝6﹣3（2x﹣1），
2x+2＝6﹣6x+3，
2x+6x＝6+3﹣2，
8x＝7，
x=78．
【点评】本题考查了解一元一次方程，解一元一次方程常见的过程有去分母、去括号、移项、合并同类项、系数化为1等．
12．（2024秋•北京期中）下面是小龙同学解方程的过程，请认真阅读并完成相应任务．
3x−14−5x−76=1．
解：3（3x﹣1）﹣2（5x﹣7）＝12…第一步
9x﹣3﹣10x﹣14＝12…第二步
9x﹣10x＝12+3+14…第三步
﹣x＝29…第四步
x＝﹣29…第五步
任务一：填空
（1）以上解题过程中，第一步是依据 等式的性质2 进行变形的；
（2）第 二 步开始出现错误，这一步的错误的原因是 去括号时，﹣2与﹣7相乘，积的符号没有变号 ；
任务二：请你求出方程正确的解．
【考点】解一元一次方程；等式的性质．
【专题】一次方程（组）及应用；运算能力．
【答案】任务一：（1）等式的性质2；
（2）二，去括号时，﹣2与﹣7相乘，积的符号没有变号；
任务二：x＝﹣1．
【分析】任务一：（1）根据等式的性质2解答即可；
（2）根据解一元一次方程的方法判断即可；
任务二：根据解一元一次方程的方法求解即可．
【解答】解：任务一：（1）在解题过程中，第一步是依据等式的性质2进行变形的．
故答案为：等式的性质2；
（2）第二步开始出现错误，错误原因是去括号时，﹣2与﹣7相乘，积的符号没有变号．
故答案为：二，去括号时，﹣2与﹣7相乘，积的符号没有变号；
任务二：3x−14−5x−76=1，
去分母，得3（3x﹣1）﹣2（5x﹣7）＝12，
去括号，得9x﹣3﹣10x+14＝12，
移项、合并同类项，得﹣x＝1，
将系数化为1，得x＝﹣1．
【点评】本题考查了解一元一次方程，等式的性质，熟练掌握解一元一次方程的方法，等式的性质是解题的关键．
13．（2024秋•北京期中）小涵在解关于x的一元一次方程3x−12+□=3时，发现正整数“□”被污染了，于是就去问同学小李，小李也记不清“□”的具体值了，只记得这个方程的解是正整数．小涵经过深入思考，想出了一个好办法，她将“□”设为m，通过计算，很快得到了□的值．你知道她是怎么计算的吗？请你求出□的值．
【考点】解一元一次方程．
【专题】一次方程（组）及应用；运算能力．
【答案】m＝2．
【分析】设□＝m，则原方程为3x−12+m＝3，解一元一次方程，可得出x=7−2m3，结合m，7−2m3均为正整数，即可得出m的值．
【解答】解：设□＝m，则原方程为3x−12+m＝3，
去分母得：3x﹣1+2m＝6，
移项、合并同类项得：3x＝7﹣2m，
将x的系数化为1得：x=7−2m3，
又∵m，7−2m3均为正整数，
∴m＝2．
【点评】本题考查了解一元一次方程，通过解一元一次方程，用含m的代数式表示出方程的解是解题的关键．
14．（2024秋•东城区校级期中）对于有理数a，b，定义了一种“⊗”的新运算，具体为：a⊗b=2a−b(a≥b)a−23b(a＜b)．
（1）计算：
①2⊗1；
②（﹣4）⊗（﹣3）．
（2）若x＝2是关于x的一元一次方程3⊗m＝﹣1+3x的解，求m的值．
【考点】一元一次方程的解；有理数的混合运算．
【专题】一次方程（组）及应用；运算能力．
【答案】（1）①3；②﹣2；（2）m的值为1．
【分析】（1）根据运算新定义计算①②即可；
（2）根据新运算定义列方程求解即可．
【解答】解：（1）①∵2＞1，
∴2⊗1＝2×2﹣1＝3；
②∵﹣4＜﹣3，
∴（﹣4）⊗（﹣3）
＝﹣4−23×(−3)
＝﹣4+2
＝﹣2．
（2）由题意得3⊗m＝﹣1+6，
即3⊗m＝5，
当3≥m时，3×2﹣m＝5，解得m＝1；
当m＞3时，3−23m=5，解得m＝﹣3（舍去）．
综上所述，m的值为1．
【点评】本题考查有理数的混合运算以及解一元一次方程，解答本题的关键是明确有理数混合运算的计算方法．
15．（2024秋•肇州县校级期中）a是最大的负整数，且a﹣2b＝﹣13，则关于x的一元一次方程x+a5−1=x−b2的解是多少？
【考点】一元一次方程的解．
【专题】一次方程（组）及应用；运算能力．
【答案】x＝6．
【分析】根据题意得a＝﹣1，进而可得b＝6，再将a＝﹣1，b＝6代入x+a5−1=x−b2即可求解键．
【解答】解：因为a是最大的负整数，所以a＝﹣1．
因为a﹣2b＝﹣13，所以b=a+132=6．
当a＝﹣1，b＝6时，原方程为：x−15−1=x−62，
解得：x＝6，
故方程x+a5−1=x−b2的解是x＝6．
【点评】本题考查一元一次方程的解，解题的关键是理解方程解的定义．
考点卡片
1．有理数
我们学习过正整数，如1，2，3，…；0；负整数，如﹣1，﹣2，﹣3，…．正整数、0、负整数统称为整数．
我们还学习过正分数，如12，23，157，0.1，5.32，0.3⋅，……；负分数，如−52，−23，−17，﹣0.5，﹣150.5，…它们都是分数．
进一步地，正整数可以写成分数的形式，例如2=21；负整数也可以写成负分数的形式，例如﹣3=−31；0也可以写成分数的形式01．这样，整数可以写成分数的形式．
可以写成分数形式的数称为有理数．其中，可以写成正分数形式的数为有理数，可以写成负分数形式的数称为负有理数．
0.1=110，﹣0.5=−12，0.3⋅=13，…，事实上，有限小数和无限循环小数都可以化分为分数，因此它们也可以看成分数．
2．有理数的混合运算
（1）有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
（2）进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．
【规律方法】有理数混合运算的四种运算技巧
1．转化法：一是将除法转化为乘法，二是将乘方转化为乘法，三是在乘除混合运算中，通常将小数转化为分数进行约分计算．
2．凑整法：在加减混合运算中，通常将和为零的两个数，分母相同的两个数，和为整数的两个数，乘积为整数的两个数分别结合为一组求解．
3．分拆法：先将带分数分拆成一个整数与一个真分数的和的形式，然后进行计算．
4．巧用运算律：在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便．
3．代数式求值
（1）代数式的值：用数值代替代数式里的字母，计算后所得的结果叫做代数式的值．
（2）代数式的求值：求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．
题型简单总结以下三种：
①已知条件不化简，所给代数式化简；
②已知条件化简，所给代数式不化简；
③已知条件和所给代数式都要化简．
4．合并同类项
（1）定义：把多项式中同类项合成一项，叫做合并同类项．
（2）合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．
（3）合并同类项时要注意以下三点：
①要掌握同类项的概念，会辨别同类项，并准确地掌握判断同类项的两条标准：带有相同系数的代数项；字母和字母指数；
②明确合并同类项的含义是把多项式中的同类项合并成一项，经过合并同类项，式的项数会减少，达到化简多项式的目的；
③“合并”是指同类项的系数的相加，并把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．
5．等式的性质
（1）等式的性质
性质1、等式两边加同一个数（或式子）结果仍得等式；
性质2、等式两边乘同一个数或除以一个不为零的数，结果仍得等式．
（2）利用等式的性质解方程
利用等式的性质对方程进行变形，使方程的形式向x＝a的形式转化．
应用时要注意把握两关：
①怎样变形；
②依据哪一条，变形时只有做到步步有据，才能保证是正确的．
6．一元一次方程的解
定义：使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解．
把方程的解代入原方程，等式左右两边相等．
7．解一元一次方程
（1）解一元一次方程的一般步骤：
去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x＝a形式转化．
（2）解一元一次方程时先观察方程的形式和特点，若有分母一般先去分母；若既有分母又有括号，且括号外的项在乘括号内各项后能消去分母，就先去括号．
（3）在解类似于“ax+bx＝c”的方程时，将方程左边，按合并同类项的方法并为一项即（a+b）x＝c．使方程逐渐转化为ax＝b的最简形式体现化归思想．将ax＝b系数化为1时，要准确计算，一弄清求x时，方程两边除以的是a还是b，尤其a为分数时；二要准确判断符号，a、b同号x为正，a、b异号x为负．