江苏省连云港市灌云县实验中学2023-2024学年九年级上学期12月月考数学试题（解析版）-A4

这是一份江苏省连云港市灌云县实验中学2023-2024学年九年级上学期12月月考数学试题（解析版）-A4，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（时间：120分钟 分值：150分）
一、选择题（每小题3分，共计24分）
1. 抛掷一枚质地均匀的硬币，若抛掷10次都是正面朝上，则抛掷第11次（ ）
A. 正面朝上的可能性大B. 反面朝上的可能性大
C. 正面朝上与反面朝上的可能性一样大D. 无法确定
【答案】C
【解析】
【分析】本题考查了概率，大量重复试验事件发生的频率接近事件发生的可能性的大小（概率）．根据大量重复试验事件发生的频率接近事件发生的可能性的大小（概率），可得答案．
【详解】解：虽然抛掷一枚质地均匀的硬币，若抛掷10次都是正面朝上，
但抛掷第11次正面朝上与反面朝上的可能性也一样大．
故选：C．
2. 正方形地板由9块边长均相等的小正方形组成，米粒随机地撒在如图所示的正方形地板上，那么米粒最终停留在黑色区域的概率是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】求出黑色方砖在整个地板中所占的面积的比值即可解决问题；
【详解】∵由图可知，黑色方砖2块，共有9块方砖，
∴黑色方砖在整个地板中所占的面积的比值＝，
∴米粒停在黑色区域的概率是．
故选B．
【点睛】本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
3. 抛物线的顶点坐标是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】已知抛物线的顶点式，可直接写出顶点坐标．
【详解】解：抛物线的顶点坐标是，
故选：A．
【点睛】本题考查了二次函数顶点式，的顶点坐标为，掌握顶点式求顶点坐标是解题的关键．
4. 已知二次函数，当时，y随x增大而减小，则实数a的取值范围是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据二次函数的增减性进行解答即可．
【详解】解：∵二次函数，当时，y随x增大而减小，
∴，
解得：，故B正确．
故选：B．
【点睛】本题主要考查了二次函数的性质，解题的关键是熟练掌握二次函数的增减性，当a>0时，在对称轴的左侧y随x的增大而减小，在对称轴的右侧y随x的增大而增大；当时，在对称轴的左侧y随x的增大而增大，在对称轴的右侧y随x的增大而减小．
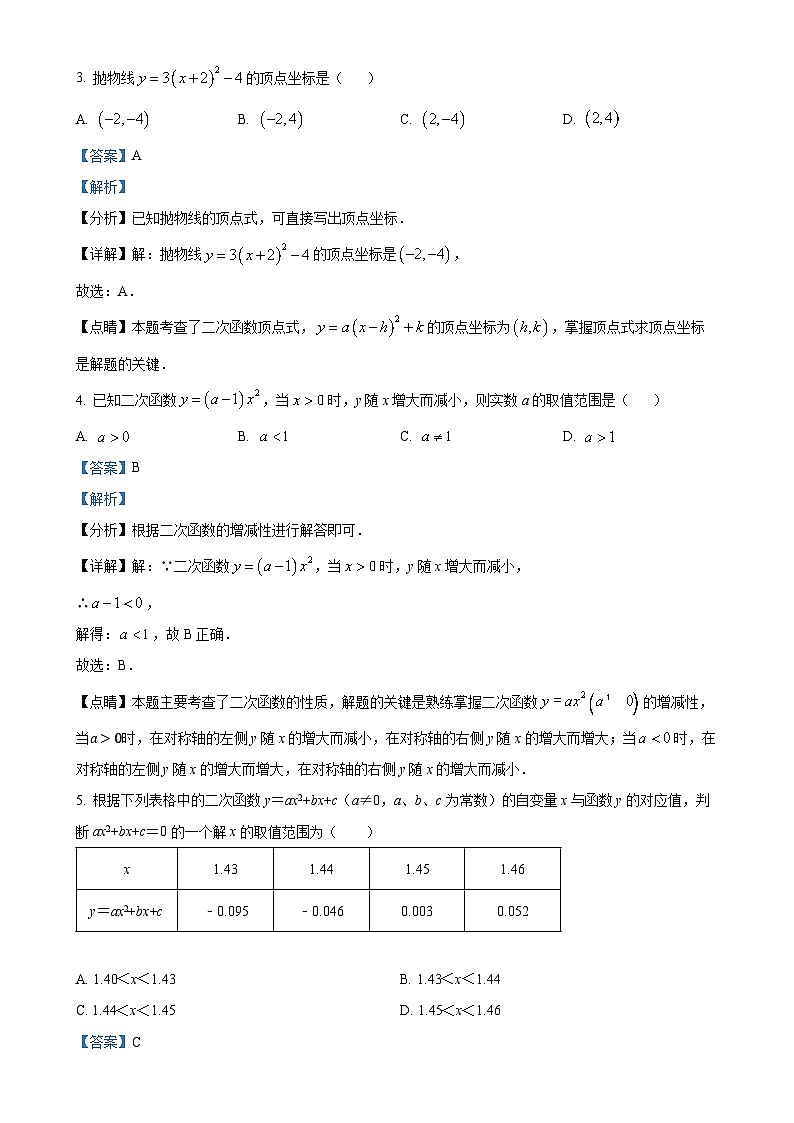
5. 根据下列表格中的二次函数y＝ax2+bx+c（a≠0，a、b、c为常数）的自变量x与函数y的对应值，判断ax2+bx+c＝0的一个解x的取值范围为（ ）
A. 1.40＜x＜1.43B. 1.43＜x＜1.44
C. 1.44＜x＜1.45D. 1.45＜x＜1.46
【答案】C
【解析】
【分析】利用表格中判断y=0的位置在-0.046与0.003之间，即可确定x的值在1.44与1.45之间.
【详解】解：由表可以看出，当x取1.44与1.45之间的某个数时，y＝0，即这个数是ax2+bx+c＝0的一个根．
ax2+bx+c＝0的一个解x的取值范围为1.44＜x＜1.45．
故选C．
【点睛】此题考查利用表格求二次函数的对应值，首先找到y=0的位置是解题关键.
6. 二次函数y=﹣x2+2x的图象可能是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】利用排除法解决：首先由a=﹣1＜0，可以判定抛物线开口向下，去掉A、C；再进一步由对称轴x=﹣=1，可知B正确，D错误；由此解决问题．
【详解】∵y=﹣x2+2x，a＜0，
∴抛物线开口向下，A、C不正确，
又∵对称轴x=﹣=1，而D的对称轴是x=0，
∴只有B符合要求．
故选B．
7. 若为二次函数图象上的三点，则的大小关系是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查了二次函数的图象性质，根据开口方向以及对称轴的位置，分析的大小，即可作答．
【详解】解：∵
∴开口向上，
∴越靠近对称轴的所对应的值越小，
∵，且比2更靠近对称轴，
∴
故选：D
8. 二次函数的图象如图所示，下列结论：①；②；③m为任意实数，则；④；⑤若且，则．其中正确的有（ ）
A. ①④B. ③④C. ②⑤D. ②③⑤
【答案】C
【解析】
【分析】根据抛物线开口方向得到，由抛物线对称轴为直线，得到，即，由抛物线与y轴的交点位置得到，所以，根据二次函数的性质可得当时，函数最大值，则当时，，再根据抛物线的对称性和抛物线与x轴的交点坐标判断即可得到结论；
【详解】∵抛物线开口向下，
∴，
∵抛物线对称轴为直线，
∴，即，故②正确；
∵抛物线与y轴的交点在x轴上方，
∴，
∴，故①错误；
∵抛物线对称轴为直线，
∴函数最大值，
∴当时，
，
即，故③错误；
∵抛物线与x轴的一个交点在的左侧，而对称轴为直线，
∴抛物线与x轴的另一个交点在的右侧，
∴当时，，
∴，故④错误；
∵，
∴，
∴，
∴，
而，
∴，即，
∵，
∴，故⑤正确；
综上所述，正确的有②⑤．
故答案选C．
【点睛】本题主要考查了二次函数图象与系数的关系，准确分析判断是解题的关键．
二、填空题（每小题3分，共计30分）
9. 投掷一枚质地均匀的骰子，落地后朝上的点数不超过4的概率为______；
【答案】
【解析】
【分析】本题主要考查了简单的概率计算，用点数不超过4的结果数除以点数朝上的所有结果数即可得到答案．
【详解】解：∵投掷一枚质地均匀的骰子，朝上的点数一共有6种情况，其中朝上的点数不超过4的情况有4种，且朝上的点数的6种情况是等可能性的，
∴落地后朝上的点数不超过4的概率为，
故答案为：．
10. 若一组数据2，3，4，m的众数为3，则这组数据的方差是______；
【答案】##
【解析】
【分析】本题主要考查众数和方差，先根据众数的概念得出，再依据方差的定义计算可得．
【详解】解：∵数据2，3，4，m众数是3，
∴，
则数据为2、3、3、4，
∴这组数据平均数为，
∴这组数据的方差为，
故答案为：．
11. 已知是二次函数，则m的值为______；
【答案】
【解析】
【分析】本题考查了二次函数的定义，形如的式子，叫二次函数，据此即可作答．
【详解】解：∵是二次函数，
∴
∴
故答案为：
12 将抛物线y＝2x2向右平移1个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为_____．
【答案】y＝2（x﹣1）2+3
【解析】
【分析】用顶点式表达式，按照抛物线平移的公式即可求解．
【详解】y＝2x2向右平移1个单位长度，再向上平移3个单位长度后，函数的表达式为：y＝2（x﹣1）2+3．
故答案为y＝2（x﹣1）2+3．
【点睛】本题考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．
13. 小丽参加了某电视台的招聘考试，她在采访写作、计算机操作、创意设计这三种测试中的成绩分别是80分、85分、90分，如果这三种成绩按计算，那么小丽的最终得分为______分．
【答案】
【解析】
【分析】根据加权平均数的定义进行计算即可．
【详解】解：由题意得，小丽的最终得分为分，
故答案为：．
【点睛】本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
14. 若函数的图像与轴没有公共点，则的取值范围是_______．
【答案】
【解析】
【分析】根据二次函数与轴没有公共点，得到，代值确定关于的不等式，求解即可得到答案．
【详解】解：函数的图像与轴没有公共点，
，
解得：，
故答案为：．
【点睛】本题考查二次函数与轴交点情况与判别式的关系，熟记二次函数与轴没有公共点时是解决问题的关键．
15. 如图，二次函数的图象过点，对称轴为直线，则关于的方程的根为________．

【答案】，
【解析】
【分析】观察函数图象当时，，由二次函数对称轴为直线，则当时，，据此即可得出方程的解．
【详解】解：根据二次函数图象可得：当时，，
又因为二次函数关于直线对称，
所以当时，，
所以关于的方程的解为，，
故答案为：，．
【点睛】本题考查根据二次函数图象确定相应方程根的情况，明确题意，运用二次函数的对称性是解题关键．
16. 如图是一座截面为抛物线的拱形桥，当拱顶离水面3米高时，水面宽为6米，则当水面下降______米时，水面宽度为米．

【答案】
【解析】
【分析】如图所示，建立平面直角坐标系，求出抛物线解析式，根据题意，令即可得到答案．
【详解】解：如图所示，建立如下平面直角坐标系：

设抛物线的解析式为，
将代入解析式得到，解得，
，
根据题意，当时，，
此时，水面下降（米），
故答案为：．
【点睛】本题考查二次函数解决实际问题，读懂题意，建立平面直角坐标系求出抛物线解析式是解决问题的关键．
17. 如图，的半径为2，是函数的图象，是函数的图象，是函数的图象，则阴影部分的面积是______．

【答案】
【解析】
【分析】本题主要考查了求扇形面积，二次函数与几何综合，根据对称性得到阴影部分面积就是一个圆心角度数为，半径为2的扇形面积是解题的关键．
【详解】解：抛物线与抛物线的图象关于x轴对称，直线与x轴的正半轴的夹角为，且抛物线和抛物线的图象自身都关于y轴对称，
∴根据图形的对称性，把左边阴影部分的面积对折到右边，可以得到阴影部分面积就是一个扇形面积，并且扇形的圆心角为，半径为2，
∴
故答案为；．
18. 如图，在第一象限内作与轴的夹角为的射线，在射线上取一点，过点作轴于点．在抛物线上取一点，在轴上取一点，使得以为顶点的三角形与全等，则符合条件的点A的坐标是______．

【答案】或或或
【解析】
【分析】此题应分四种情况考虑：（1）当，时；（2）当，时；（3）当，时；（4）当，时，利用特殊三角形三边关系，根据三角形全等即可求解．
【详解】（1）当，时，

设，代入，
解得：（舍去），，
，，
又，
，，
；
（2）当，时，

过点作轴，垂足为，
由（1）得，，，
由勾股定理得：，
在中，由勾股定理得：，
又，
，
；
（3）当，时，

设，代入，解得：（舍去），，
，，
，
，
，
；
（4）当，时，

过点作轴，垂足为点，
由（3）得，，
在中，由勾股定理得：，
在中，，，
由勾股定理得：，
又，
，
，
，
综上所述，点A的坐标是或或或．
【点睛】本题主要考查是全等三角形的判定和性质以及二次函数图象和性质，由于全等三角形的对应顶点不明确，因此要注意分类讨论思想的运用．
三、解答题（本大题共8小题，共计96分）
19. 已知抛物线的顶点坐标为，且经过轴上一点．
（1）求抛物线解析式；
（2）若抛物线与x轴的另一个交点记为，求出的面积．
【答案】（1）
（2）27
【解析】
【分析】本题主要考查了待定系数法求二次函数解析式、二次函数综合应用等知识，解题关键是运用数形结合的思想分析问题．
（1）结合题意，设抛物线解析式为，然后将点代入求解即可；
（2）过点作交于，连接，首先计算点坐标，再求得的长度，然后根据三角形面积公式求解即可．
【小问1详解】
解：∵抛物线的顶点坐标为，
∴设抛物线解析式为，
∵图像经过，
∴可有，
解得
∴抛物线解析式为；
【小问2详解】
如下图，过点作交于，连接，
令，
解得，
∴，
∴，
∵，
∴，
∴．
20. 宿迁具有丰富的旅游资源，小明利用周日来宿迁游玩，上午从A、B、C三个景点中任意选择一个游玩，下午从D、E两个景点中任意选择一个游玩．
（1）求上午小明选中景点A的概率；
（2）用列表或画树状图的方法列出所有等可能的结果，并求小明恰好选中景点B和D的概率．
【答案】（1）；（2）
【解析】
【分析】（1）直接利用概率公式求解即可；
（2）用列表法即可得到小陈所有可能的游玩方式，从中得出恰好选中B、E的情况占总情况的多少即可．
【详解】解：（1）上午小明选中景点A的概率为；
（2）列表如下：
由表可知，共有6种等可能结果，其中小明恰好选中景点B和D的只有1种结果，
∴小明恰好选中景点B和D的概率为．
【点睛】本题考查了列表法求概率，解答的关键是熟练掌握列表法是可以不重复不遗漏的列出所有可能的结果适合于两步完成的事件，解题时还要注意是放回实验还是不放回实验，概率公式为：概率=所求情况数与总情况数之比．
21. 某校学生会向全校3000名学生发起了“爱心捐助”捐款活动，为了解捐款情况，学生会随机调制了如图的统计图．

请根据相关信息，解答下列问题：
（1）本次接受随机调查的学生人数为 ，图1中m的值是 ；
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
【答案】（1）50人，32
（2）16元，10元，15元
（3）960人
【解析】
【分析】（1）由捐款5元的人数及其所占百分比可得总人数，再用捐款10元的人数除以总人数可得的值；
（2）根据平均数、众数和中位数的概念求解可得答案；
（3）用总人数乘以样本中捐款10元的人数所占比例即可．
【小问1详解】
解：本次接受随机调查的学生人数为（人），
，即，
故答案为：50人，32；
【小问2详解】
本次调查获取的样本数据的平均数是：（元），
本次调查获取的样本数据的众数是：10元，
本次调查获取的样本数据的中位数是：15元；
【小问3详解】
估计该校本次活动捐款金额为10元的学生人数为（人）．
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数，解题的关键是明确题意，找出所求问题需要的条件．
22. 已知二次函数．
（1）求函数图象的顶点坐标，并画出这个函数的图象；
（2）根据图象，直接写出：
①当函数值y为负数时，自变量x的取值范围是______；
②当时，函数值y的取值范围是______．
【答案】（1），函数的图象见解析
（2）①或，②
【解析】
【分析】本题考查了画二次函数图象，化为顶点式，根据函数图象求不等式的解集，数形结合是解题的关键．
（1）将二次函数解析式化为顶点式，求得顶点坐标，根据描点法画出二次函数图象即可求解；
（2）①根据函数图象直接写出函数值y为负数时，自变量x的取值范围；②根据二次函数的性质得出取得最小值，顶点位置取得最大值，据此即可求解．
【小问1详解】
解：∵，
∴函数图象的顶点坐标1,4；
列表如下，
函数的图象如图：
【小问2详解】
解：根据图象可知：
①当或时，函数值y为负数，
故答案为：或；
②，图象开口向下，又，
当时，取得最小值，，
∵顶点坐标为1,4，则最大值为4，
当时，函数值y的取值范围，
故答案为：．
23. 2023年第十九届亚运会在杭州举行，这是我国第三次举办亚运会，在中国队对阵韩国队的男篮四分之一决赛中，中国队表现出色，赢得了比赛．如图，一名中国运动员在距离篮球框中心A点（水平距离）远处跳起投篮，篮球准确落入篮框，已知篮球运行的路线为抛物线，当篮球运行水平距离为时，篮球达到最大高度B点处，且最大高度为，以地面水平线为x轴，过最高点垂直地面的直线为轴建立平面直角坐标系，如果篮框中心距离地面．
（1）求该篮球的运行路线（抛物线）的表达式；
（2）求出篮球在该运动员出手时的高度．
【答案】（1）
（2）米
【解析】
【分析】本题主要考查了二次函数的实际应用，明确题意，准确求出函数解析式是解题的关键．
（1）运用待定系数法求二次函数的解析式，先设，代入，即可作答．
（2）已知，令，算出对应的值，即可作答．
【小问1详解】
解：根据题意得：，，点C的横坐标为．
设y与x满足的函数解析式为，
把点代入得：，
解得：，
∴y与x满足的函数解析式为；
【小问2详解】
解：由（1）知
令，则，
∴篮球在该运动员出手时的高度是米．
24. 某商家销售一种成本为30元的商品销售一段时间后发现，每天的销量（件）与当天的销售单价（元件）满足的函数关系为，物价部门规定，该商品的销售单价不能超过60元件．
（1）问销售单价定为多少元时，商家销售该商品每天获得的利润是9000元？
（2）当销售单价定为多少元时，商家销售该商品每天获得的利润最大，并求出最大利润．
【答案】（1）销售单价定为40元件时，工艺厂试销该工艺品每天获得的利润9000元
（2）销售单价定为60元时，商家销售该商品每天获得的利润最大，其最大利润为18000元
【解析】
【分析】（1）根据每件的利润乘以销售量等于总利润，列出方程，即可求解；
（2）根据每件的利润乘以销售量等于总利润，列出函数关系式，再根据二次函数的性质，即可求解．
【小问1详解】
解：根据题意，得，
整理，得，
解得，，
销售单价最高不能超过60元件，
，
答：销售单价定为40元件时，工艺厂试销该工艺品每天获得的利润9000元；
【小问2详解】
解：设销售利润为元，
则，
，且销售单价最高不能超过60元件，
当时，取最大值为：18000，
故当销售单价定为60元时，商家销售该商品每天获得的利润最大，其最大利润为18000元．
【点睛】本题主要考查了一元二次方程的应用，二次函数的实际应用，明确题意，准确得到等量关系是解题的关键．
25. 二次函数的图像是抛物线，定义一种变换，先作这条抛物线关于原点对称的抛物线，再将得到的对称抛物线向上平移个单位，得到新的抛物线，我们称叫做二次函数的阶变换．
（1）二次函数的顶点关于原点的对称点为______，这个抛物线的2阶变换的解析式为______；
（2）若二次函数的5阶变换的关系式为．
①二次函数的解析式为______；
②若二次函数的顶点为点，与轴相交的两个交点中右侧交点为，是轴上的一个动点，请求出使周长最小时，点的坐标．
【答案】（1），
（2）①②
【解析】
【分析】（1）根据二次函数的性质求出其顶点坐标，再根据关于原点对称的点的坐标特点，写出其关于原点的对称点的坐标，根据定义即可求解解析式；
（2）①将抛物线向下平移5个单位得到，此时该抛物线的顶点坐标为，该点关于原点的对称点为，进而求解；②首先求得抛物线的顶点的坐标，点的坐标，并求得点关于轴的对称点的坐标，当点三点共线时，的周长最小，利用待定系数法解得直线的解析式，进而确定点的坐标即可．
【小问1详解】
解：二次函数的顶点坐标为，
∴该点关于原点的对称点为，
作这条抛物线关于原点对称的抛物线，
则有，
将抛物线向上平移2个单位长度，
可得，
所以原抛物线的2阶变换的解析式为
故答案为：，；
【小问2详解】
①将抛物线向下平移5个单位得到，
此时该抛物线顶点坐标为，
该点关于原点的对称点为，
即二次函数的顶点坐标为，
∴二次函数的解析式为．
故答案为：；
②如下图，
对于抛物线：，
其顶点坐标的坐标为，
令，可有，
解得，，
∵与轴相交的两个交点中右侧交点为，
∴，
作点关于轴的对称点，则，
∴，
∴周长，
∴当点三点共线时，的周长最小，
设直线的解析式为，
将点，代入，
可得，解得，
∴直线的解析式为，
令，则有，
∴点的坐标为．
【点睛】本题主要考查了新定义“二次函数的阶变换”、求关于原点对称的点的坐标、二次函数的图像与性质、关于轴对称的点的坐标特征、待定系数法求一次函数解析式、一次函数图像与坐标轴交点等知识，解题关键是掌握相关知识，并运用数形结合的思想分析问题．
26. 如图，直线与轴交于点，与轴交于点，经过两点的抛物线与轴的另一个交点为．
（1）求抛物线的解析式；
（2）点是直线上方抛物线上的一个动点，过点作轴的平行线交直线于点，当面积最大时，求出点的坐标；
（3）在（2）的结论下，连接，点是抛物线对称轴上的动点，在抛物线上是否存在点，使得以为顶点的四边形是平行四边形？如果存在，请直接写出点的坐标：如果不存在，请说明理由．
【答案】（1）
（2）
（3）或或
【解析】
【分析】（1）令，则，即点，点B0,3，将点，点B0,3代入抛物线，即可求解；
（2）由，设点，则，求出利用二次函数的性质即可求解；
（3）分当是平行四边形的一条边、是平行四边形的对角线两种情况，分别求解即可．
【小问1详解】
解：直线与轴交于点，与轴交于点，
当时，，当时，，
B0,3，，
将B0,3，代入，得：，
解得：，
抛物线的解析式为：；
【小问2详解】
解：由（1）知抛物线的解析式为：，
设点，则，
，
，
，
当时，面积最大，
；
【小问3详解】
解：，
抛物线的对称轴为：，
令，则，
解得：，
，
，
设点，点，
①当是平行四边形的一条边时，
当点P在对称轴的右侧时，
点M向左平移个单位向下平移个单位得到A，
同理向左平移个单位向下平移个单位得到，
即，解得：，故点；
当点P在对称轴的左侧时，
同理可得点；
②当是平行四边形的对角线时，
的中点坐标为，此坐标即为P，Q的中点坐标，
即，解得：，故点；
综上，点P的坐标为或或．
x
1.43
1.44
1.45
1.46
y＝ax2+bx+c
﹣0.095
﹣0.046
0.003
0.052
D
E
A
（A，D）
（A，E）
B
（B，D）
（B，E）
C
（C，D）
（C，E）
x
⋅⋅⋅
0
1
2
3
4
⋅⋅⋅
⋅⋅⋅
0
3
4
3
0
⋅⋅⋅